DBMS 인덱스 이야기

jy.YOON·2022년 10월 13일

DataBase

목록 보기

2/2

DB의 성능 튜닝은 어떻게 디스크 I/O를 줄이느냐가 관건.

일반적으로 쿼리를 튜닝하는것은 랜덤I/O 자체를 줄여주는 것이 목적.

랜덤I/O와 순차I/O

디스크의 성능은 디스크 헤더의 위치 이동 없이 얼마나 많은 데이터를 한 번에 기록하느냐에 의해 결정된다.

그래서 위 그림을 봤을때는 디스크의 헤더의 위치가 바뀔 가능성이 많은 랜덤 접근(Random access) 보단 순차적 접근(Sequential access)이 더 빠르다 볼 수 있다.

그래서

여러 번 쓰기 또는 읽기를 요청하는 랜덤I/O 작업이 작업 부하가 훨씬 더 크다.

HDD와 SSD

DB 서버 에서는 항상 디스크 장치가 항상 병목이 된다.

HDD는 원판에 의해서 기계적으로 회전시키지만,

SSD는 원판을 제거하고 그 대신 플래시 메모리를 장착하고 있으며, 기계적으로 원판을 회전 시킬 필요가 없어 데이터를 빨리 읽고 사용할 수 있다.

플래시 메모리

전원이 공급되지 않아도 데이터가 삭제되지 않음

디스크 헤더를 움직이지 않고 한번에 많은 데이터를 읽는 순차I/O 는

SSD 가 HDD보다 조금 빠르거나 비슷한 성능을 보이기도 한다.

하지만

SDD의 장점은 기존 HDD 드라이브 보다 랜덤I/O가 빠르다는 것이다.

랜덤I/O를 통해 작은 데이터를 읽고 쓰는 작업이 대부분이므로 SSD의 장점은

DBMS용 스토리지에 최적이라고 볼수 있다.

인덱스

컬럼의 값과 해당 래코드가 저장된 주소를 키와 값의 쌍으로 삼아 인덱스를 만들어 두는 것이다.

결론적으로 DBMS에서 인덱스는 데이터의 저장(Insert, Update, Delete) 성능을 희생하고 그 대신 데이터의 읽기 속도를 높이는 기능이다.

인덱스 추가시에는 데이터의 저장 속도를 어디까지 희생할 수 있는지, 읽기 속도를 얼마나 더 빠르게 만들어야 하느냐를 고려해야 한다.

인덱스를 남발하면 오히려 저장성능이 떨어지고 인덱스의 크기가 비대해져 오히려 역효과만 불러올 수 있다.

인덱스의 데이터 저장방식

1.B-Tree 인덱스

B-Tree 에서 B는 Balanced 를 의미하며 균형 이진트리라고 한다.

이진트리 기반의 트리. 최악에서도 log(N)의 성능을 보장

2개 이상의 자식들을 가질수 있기 때문에 많은 데이터를 가질 수 있다는것이 장점

대량의 데이터는 메모리에 저장되는것이 아닌 블럭 단위로 입출력하는 하드디스크 or SSD 에 저장됨

ex) 한 블럭이 1024 바이트면, 2바이트를 읽으나 1024바이트를 읽으나 똑같은 입출력 비용 발생. 따라서 하나의 노드를 모두 1024바이트로 꽉 채워서 조절할 수 있으면 입출력에 있어서 효율적인 구성을 갖출 수 있다

이러한 장점 때문에 많은 DBMS 에서는 인덱스 저장 방법으로 사용하고 있음

내부적으로 B-Tree 또는 B+Tree 가 사용되고 있는데. 그 둘을 비교해보자.

B-Tree

1.B-tree는 각 노드에서 key와 data 모두 들어갈 수 있고, data는 disk block으로 포인터가 될 수 있음

B+Tree

B+tree는 리프 노드를 제외하고는 데이터를 담아두지 않기 때문데 메모리를 더 확보함으로써 많은 key들을 수용할 수 있다.
하나의 노드에 많은 key들을 담을 수 있기 때문에 트리의 높이가 낮아짐으로 cache hit를 높일 수 있다.
풀 스캔시 B+Tree는 리프노드에 데이터가 모두 있기 때문에 한 번의 선형 탐색만 하면 되기 떼문에 B-Tree에 비해 빠르다.(리프노드 끼리 서로 링크드리스트로 연결되어있음)

cache hit

CPU가 참조하고자 하는 메모리가 캐시에 존재하고 있을 경우 Cache hit 라고 한다.

2.Hash 인덱스

컬럼의 값을 해시값으로 계산해서 인덱스하는 알고리즘

검색에 최적화된 인덱스

주로 메모리 기반의 테이블에서 사용된다.

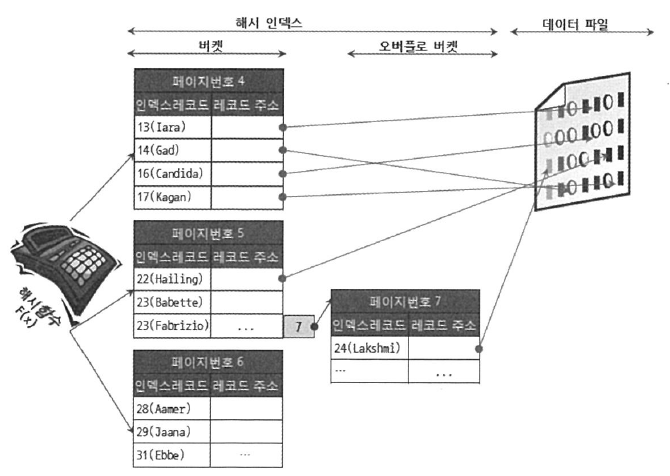
1.해시 인덱스의 큰 장점은 실제 키값과는 관계없이 인덱스 크기가 작고 검색이 빠르다는 것이다.

2.트리형태의 구조가 아니며 검색하고자 하는 값을 해시 함수를 거쳐서 찾고자 하는 키값이 포함된 버켓을 알아내

그 버켓 하나만 읽어서 비교하여 실제 레코드가 저장된 위치를 바로 알아낸다.

3.특정 조건으로 읽는다면 B-Tree보다 상당히 빠른 결과를 가져온다.

4.그러나 범위가 넓으면 그만큼 버켓이 많이 필요해지기 때문에 공간의 낭비가 커지며,

값의 범위가 너무 작으면 해시 충돌의 경우가 발생하여 해시 인덱스의 장점이 사라진다.

5.범위 검색(>=, Between And, <>, LIKE )보다는 동등비교조건(==, IN, IS NULL, IS NOT NULL, <=>) 에서 효과를 얻을 수 있다.

해시충돌

다른 내용의 데이터가 같은 키를 갖는다면? 이러한 상황을 해시 충돌(Hash Collision)이라고 한다. 같은 키값을 갖는 데이터가 생긴다는 것은, 특정 키의 버켓에 데이터가 집중된다는 뜻이다

위의 그림에서 Sandra Dee라는 사람의 연락처를 삽입하는 상황을 가정해보자. Sandra Dee라는 키는 John Smith라는 키와 결과값이 같다. 둘 사이에 충돌이 일어난 것이다. 그러자 충돌이 일어난 주소(혹은 색인)의 bucket에 레코드가 추가로 담긴 것을 확인할 수 있다. 만약에 해당 bucket에 충분한 공간이 없다면? 오버플로우가 발생한다.

해시 충돌을 해결하는 방법

1.체이닝

버켓 내에 연결리스트(Linked List)를 할당하여, 버켓에 데이터를 삽입하다가 해시 충돌이 발생하면 연결리스트로 데이터들을 연결하는 방식이다. 그림2를 다시보자, Sandra Dee라는 사람의 연락처를 삽입할 때, 충돌이 일어나니 버켓 내에서 연결리스트로 데이터를 연결하는 것을 확인할 수 있다.

2.개방 주소법

체이닝의 경우 버켓이 꽉 차더라도 연결리스트로 계속 늘려가기에, 데이터의 주소값은 바뀌지 않는다.(Closed Addressing) 하지만 개방 주소법의 경우에는 다르다. 해시 충돌이 일어나면 다른 버켓에 데이터를 삽입하는 방식을 개방 주소법이라고 한다. 개방 주소법은 대표적으로 3가지가 있다.