그래프의 각 정점을 방문하는 그래프 순회 (Graph Traversals)에는 크게 DFS, BFS 의 2가지 방법이 있음
✔그래프 python 구현
다음과 같이 그래프를 인접리스트를 사용하여 표현
graph = {1: [2, 3, 4], 2: [5], 3: [5], 5: [6, 7], 7: [3]})
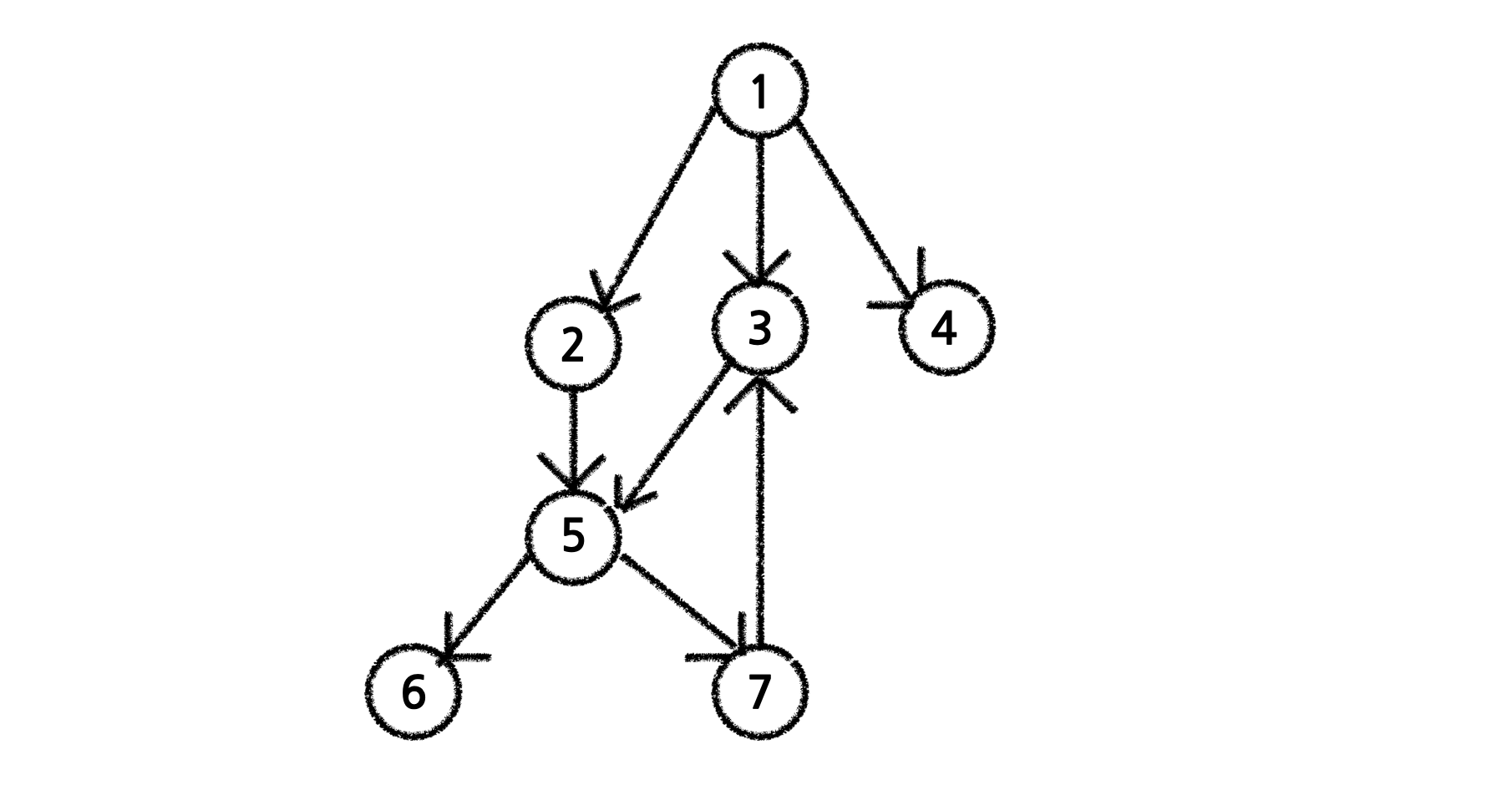
from collections import defaultdict, deque
class Graph:
def __init__(self, edge_list):
self.graph = defaultdict(list)
for v1, v2 in edge_list:
self.graph[v1].append(v2)
if __name__ == '__main__':
g = Graph([[1, 2], [1, 3], [1, 4], [2, 5], [3, 5], [5, 6], [5, 7], [7, 3]])
print(g.graph) #defaultdict(<class 'list'>, {1: [2, 3, 4], 2: [5], 3: [5], 5: [6, 7], 7: [3]})📘 DFS(깊이 우선 탐색)
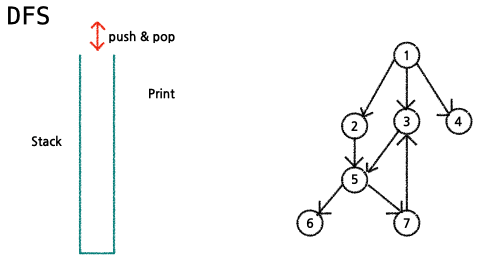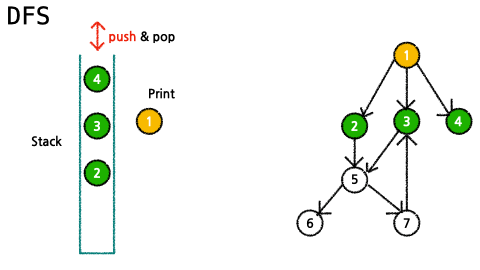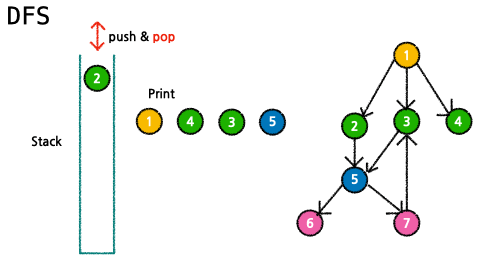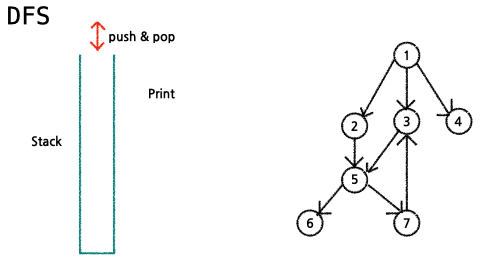
임의의 노드에서 출발하여 해당 branch의 리프노드가 나올때까지 탐색 후, 다음 brunch로 넘어가서 반복하여 모든 정점을 탐색하는 방법
✔ 이론
- stack에서 node를 꺼내서 출력
- 꺼낸 node의 child node들을 stack에 추가한다.
(단,child node를 넣을 때, 출력되었던 node는 추가하지 않는다.)
✔ 구현_1 (stack 자료구조 사용)
- 탐색한 node들을 표시해줄 빈 리스트 visited 선언하고 stack에 시작점을 추가한다.
- stack에 데이터가 없을 때까지 다음과 같은 과정을 반복한다.
- 가장 최근에 넣은 데이터 pop()
- pop()한 데이터가 visited에 없을 경우(탐색하지 않은 데이터일 경우) visited에 추가하고, 해당 데이터(노드)의 child 노드들을 stack에 추가
- visited(탐색 한 데이터를 담은 list) 반환
from collections import defaultdict, deque
class Graph:
def __init__(self, edge_list):
self.graph = defaultdict(list)
for v1, v2 in edge_list:
self.graph[v1].append(v2)
#DFS stack구현
def dfs_stack(self, start_v = 1):
visited = []
stack = [start_v]
while stack:
node = stack.pop()
if node not in visited:
visited.append(node)
stack.extend(self.graph[node])
return visited
if __name__ == '__main__':
g = Graph([[1, 2], [1, 3], [1, 4], [2, 5], [3, 5], [5, 6], [5, 7], [7, 3]])
print(g.graph) #defaultdict(<class 'list'>, {1: [2, 3, 4], 2: [5], 3: [5], 5: [6, 7], 7: [3]})
print(g.dfs_stack()) #[1, 4, 3, 5, 7, 6, 2]✔ 구현_2 (recursion 사용)
stack구현과 같은 방법이지만 반복문(while stack:)을 사용하지 않고 재귀를 사용하여 구현.
from collections import defaultdict, deque
class Graph:
def __init__(self, edge_list):
self.graph = defaultdict(list)
for v1, v2 in edge_list:
self.graph[v1].append(v2)
#DFS recursion구현
def dfs_recursion(self, node = 1, visited = []):
visited.append(node)
for v in self.graph[node]:
if v not in visited:
self.dfs_recursion(v, visited)
return visited
if __name__ == '__main__':
g = Graph([[1, 2], [1, 3], [1, 4], [2, 5], [3, 5], [5, 6], [5, 7], [7, 3]])
print(g.graph) #defaultdict(<class 'list'>, {1: [2, 3, 4], 2: [5], 3: [5], 5: [6, 7], 7: [3]})
print(g.dfs_recursion()) #[1, 2, 5, 6, 7, 3, 4]📝 똑같은 DFS인데 순서가 다른 이유
print(g.dfs_stack()) #stack 구현 출력: [1, 4, 3, 5, 7, 6, 2]
print(g.dfs_recursion()) #recursion 구현 출력[1, 2, 5, 6, 7, 3, 4]dfs_recursion은 child node를 사전식 순서대로 방문 하지만 dfs_stack에서 stack은 LIFO구조 이므로 node를 사전식 순서의 역순으로 방문하기 때문
📘 BFS(너비 우선 탐색)
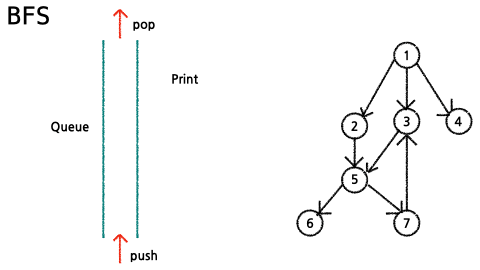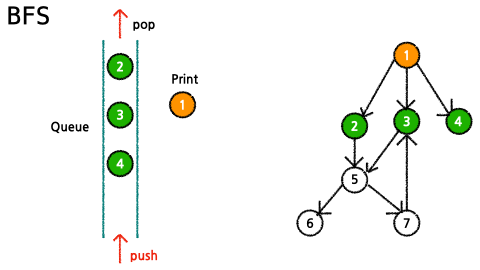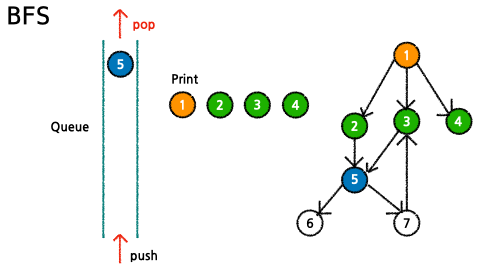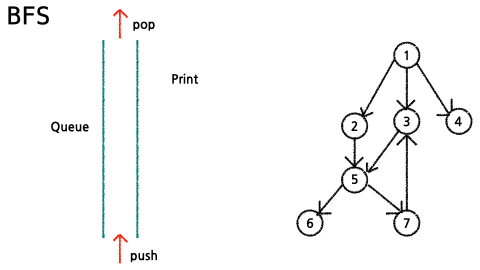
임의의 노드에서 출발하여 해당 level의 정점들을 모두 탐색한 뒤, 그 다음 level을 탐색하는 것을 반복하여 모든 정점들을 탐색
✔ 이론
- queue에서 node를 꺼내서 출력
- 꺼낸 node의 child node들을 queue에 추가한다.
(단,child node를 넣을 때, 한번 넣었던 node는 추가하지 않는다.)
✔ 구현 (queue 자료구조 사용)
- queue에 시작노드를 추가하고, visited에도 시작노드를 추가하여 queue에 추가한 노드들을 표시한다.
- queue에 데이터가 없을 때까지 다음과 같은 과정을 반복한다.
- 가장 처음 넣은 데이터 pop()
- 해당 데이터(node)의 child node들 중 visited에 없는(queue에 추가 된 적 없는) 노드들을 queue에 추가하고 visited에 추가한다.
- visited(queue에 넣었 던 데이터를 담은 list) 반환
from collections import defaultdict, deque
class Graph:
def __init__(self, edge_list):
self.graph = defaultdict(list)
for v1, v2 in edge_list:
self.graph[v1].append(v2)
#BFS queue구현
def bfs_queue(self, start_v = 1):
visited = [start_v]
q = deque([start_v])
while q:
node = q.popleft()
for v in self.graph[node]:
if v not in visited:
q.append(v)
visited.append(v)
return visited
if __name__ == '__main__':
g = Graph([[1, 2], [1, 3], [1, 4], [2, 5], [3, 5], [5, 6], [5, 7], [7, 3]])
print(g.graph) #defaultdict(<class 'list'>, {1: [2, 3, 4], 2: [5], 3: [5], 5: [6, 7], 7: [3]})
print(g.bfs_queue()) #[1, 2, 3, 4, 5, 6, 7]📘 전체 소스 코드
from collections import defaultdict, deque
class Graph:
def __init__(self, edge_list):
self.graph = defaultdict(list)
for v1, v2 in edge_list:
self.graph[v1].append(v2)
#DFS stack구현
def dfs_stack(self, start_v = 1):
visited = []
stack = [start_v]
while stack:
node = stack.pop()
if node not in visited:
visited.append(node)
stack.extend(self.graph[node])
return visited
#DFS recursion구현
def dfs_recursion(self, node = 1, visited = []):
visited.append(node)
for v in self.graph[node]:
if v not in visited:
self.dfs_recursion(v, visited)
return visited
#BFS queue구현
def bfs_queue(self, start_v = 1):
visited = [start_v]
q = deque([start_v])
while q:
node = q.popleft()
for v in self.graph[node]:
if v not in visited:
q.append(v)
visited.append(v)
return visited
if __name__ == '__main__':
g = Graph([[1, 2], [1, 3], [1, 4], [2, 5], [3, 5], [5, 6], [5, 7], [7, 3]])
print(g.graph) #defaultdict(<class 'list'>, {1: [2, 3, 4], 2: [5], 3: [5], 5: [6, 7], 7: [3]})
print(g.dfs_stack()) #[1, 4, 3, 5, 7, 6, 2]
print(g.dfs_recursion()) #[1, 2, 5, 6, 7, 3, 4]
print(g.bfs_queue()) #[1, 2, 3, 4, 5, 6, 7]📝 DFS BFS에서 visited 용도
DFS : 탐색한 정점인지 아닌지 확인
BFS: queue에 넣었던 정점인지 아닌지 확인( = 탐색한 정점인지 아닌지 확인)
DFS는 stack자료구조를 사용하기 때문에 stack에 들어간 데이터들의 순서와 탐색한 데이터들의 순서가 다르다. 데이터를 꺼낼 때, 그 데이터를 탐색했다고 생각하면 이해가 편함.
BFS는 queue자료구조를 사용하기 때문에 queue에 들어간 데이터들의 순서와 탐색한 데이터들의 순서가 같다. queue에 데이터를 넣을 때, 그 데이터를 탐색했다고 생각하면 이해가 편함