코드를 짤때 무조건 짧은 코드가 좋은 코드라고 생각했을때가 있었다. 공부를 하면서 연산횟수가 적은코드가 더 좋은 코드란걸 자연스레 알게 됬었다. 그리고 그것을 시간복잡도와 관련지을수 있다.

⭐️ 시간복잡도

✅ 입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가를 시간복잡도라고 할 수 있다.

시간 복잡도 표기법

➊ Big-O(빅-오)

• 시간복잡도가 최악인 경우를 나타내는 방법.

➋ Big-Ω(빅-오메가)

• 시간복잡도가 최선 경우를 나타내는 방법.

➌ Big-θ(빅-세타)

• 시간복잡도가 평균인 경우를 나타내는 방법.

빅오 표기법은 '이정도 시간까지 걸릴 수 있다'라는 의미를 가진다.

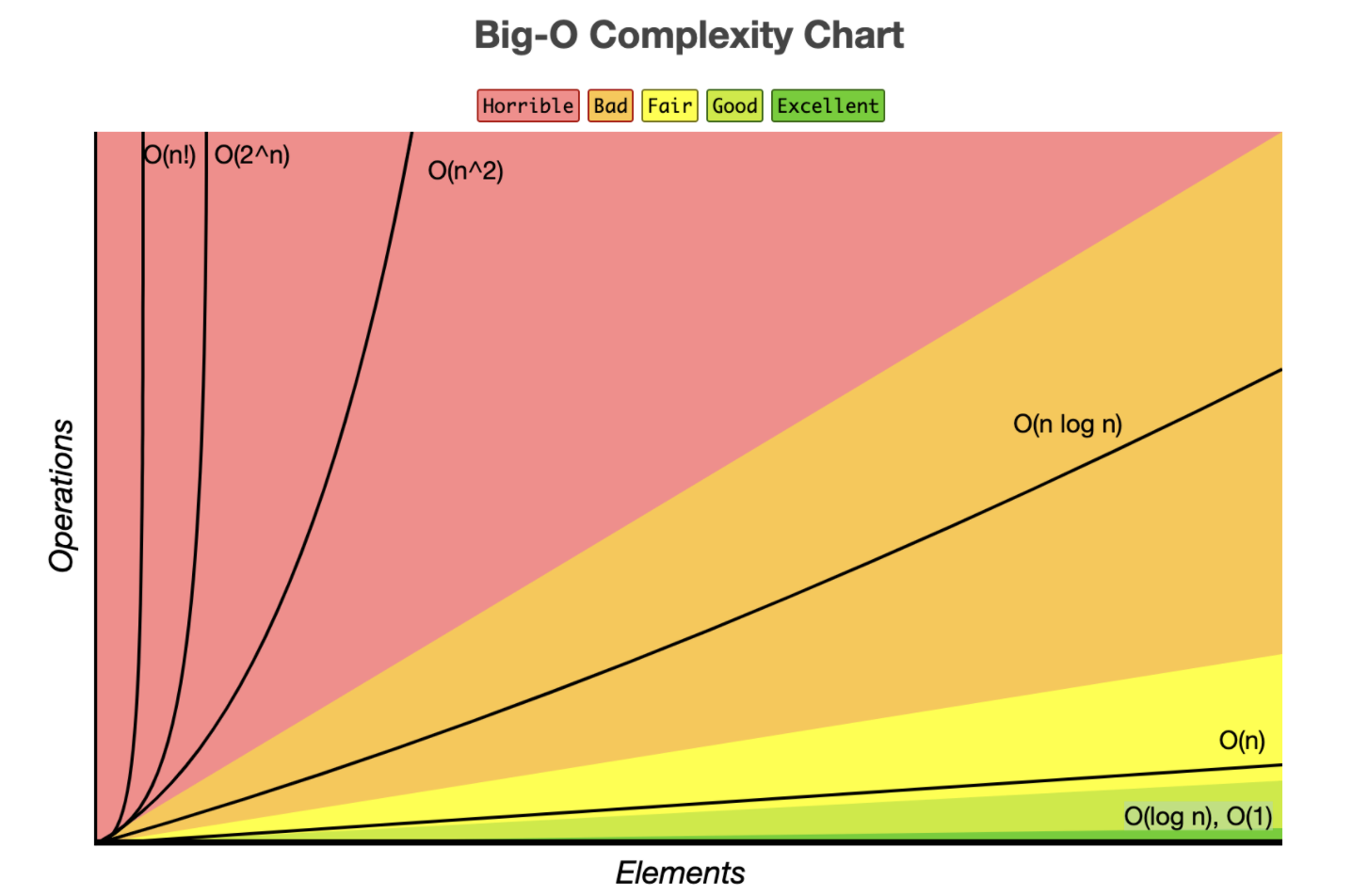
📌시간복잡도 비교표

시간	1	2	3	4	8	16	예
O(1)	1	1	1	1	1	1	해시 테이블
O(log n)	0	1	1.58	2	3	4	이진 탐색
O(n)	1	2	3	4	8	16	순차 탐색
O(n log n)	0	2	4.75	8	24	64	퀵, 합병 정렬
O(n^2)	1	4	9	16	64	256	이중 for 문
O(2^n)	2	4	8	16	256	65536	피보나치수열
O(n!)	1	2	6	24	40320	20922789888000

시간복잡도에따라 연산 횟수에 비해 시간이 급격하게 차이가 나는것을 확인 할 수있다. 이렇기 때문에 알고리즘을 작성할때 시간 복잡도를 생각해야한다. 다만.. n값이 작을 작을때는 그 차이가 크지 않기에 주의해야 한다.

😎결론! 시간복잡도 수치가 작을수록 효율적인 알고리즘이다!