그리디와 다익스트라의 문제를 풀어보는 날.
다익스트라는 처음 본 개념이다. 보다보니 BFS 너비우선탐색과도 헷갈린다. 각 알고리즘의 개념과 다익스트라 문제를 복습하며 오늘을 마무리~
BFS와 다익스트라 짚고가기
BFS
- 시작 노드로부터 인접한 모든 노드 탐색. 최단 경로를 찾는데 사용된다.
- 가중치가 없는 그래프나 가중치가 동일한 그래프에서 사용
- 시작 노드에서 인접한 노드를 모두 탐색 -> 해당 노드의 인접한 노드를 순차적으로 탐색
- queue를 사용한다.
다익스트라 알고리즘
- 주어진 시작 노드로부터 모든 노드까지의 최단 경로를 찾는데 사용
- 가중치가 있는 그래프에서 사용
- 시작 노드에서 인접한 노드로 가는 최소 비용을 유지하며 탐색
- 우선순위 queue를 사용! 최소 비용의 노드를 선택하고 인접한 노드들의 비용을 갱신하는 방식으로 구현
그리디
그리디 탐욕 알고리즘 정리
- 미래를 고려하지 않고 오직 현재 시점에 가장 좋은 선택을 하는 알고리즘
- 무조건 지금 가장 저렴하고 빠른 선택을 한다.
- 백준 11047: 동전0 최소 동전 수 구하기. 가장 대표적인 예시.
그리디 알고리즘의 특징
- 현재의 최적 해가 전체의 최적 해가 되는건 아니라서 최적의 해를 항상 보장하지 못함
- 근사 알고리즘이라고도 한다. 최적 해가 보장되는 조건에서만 사용할 수 있음
- 현재 선택이 미래의 선택에 영향을 주지 않는 경우에 사용할 수 있다.
- 부분의 최적의 해가 모이면 전체의 최적 해가 되는 경우에 사용할 수 있다.
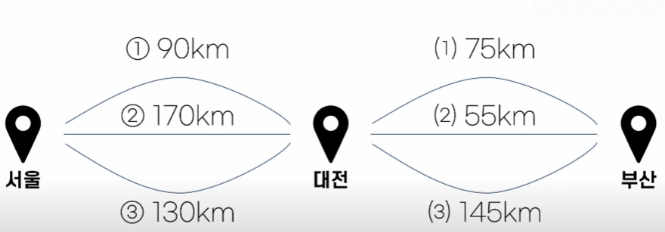
ex) 서울에서 대전을 가는 선택이 대전에서 부산을 가는 선택에 영향을 주지 않음.
그리디 문제, 접근법
- 백준 1931:회의실 배정
- 회의 시작 시간과 종료 시간을 받고 회의를 가장 많이 진행할 수 있는 경우를 구하는 문제
- 최대한 많은 회의 → 빨리 끝나는 회의 먼저 진행(정렬) → 끝난 시간보다 시작 시간이 앞선 회의는 무시 → 진행 가능한 회의 시작을 반복
그리디는 100% 최적의 해를 보장하지 않아도 되는 경우 빠르게 탐색할 수 있음이 장점!
유튜브 <개발자로 취직하기>의 추천 문제

다익스트라
- 다이나믹 프로그래밍을 이용한 최단 경로 탐색 알고리즘. 흔히 GPS 소프트웨어 등에서 많이 사용된다. 하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 알려준다.
- 최단 거리는 여러 개의 최단 거리로 이루어짐.
- 다익스트라 알고리즘은 DP와 그리디 문제로도 분류되기도 한다
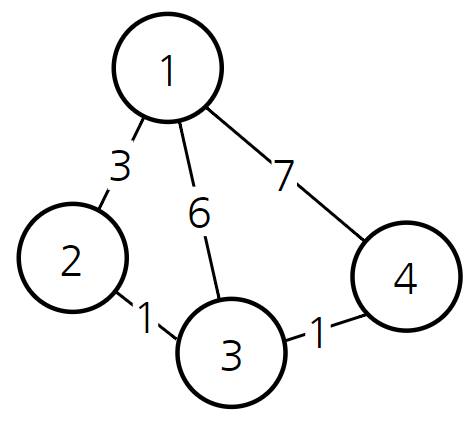
1번 노드에서 3번 노드로 가는 비용은 6.
1번 ->2번 노드에서 3번 노드로 가는 비용은 4.
알고 있던 최소 비용 6을 4로 새롭게 갱신한다.
동작 과정
- 출발 노드 설정
- 출발 기준으로 각 노드의 최소 비용을 저장
- (1) 방문하지 않은 노드 중 가장 비용이 적은 노드를 선택
- (2) 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려해서 최소 비용을 갱신
- (1)과 (2)를 반복
이 문제의 풀이를 간략히 말하면 다익스트라 알고리즘을 사용하고 costs라는 리스트를 만들어 인덱스에 해당 도시(숫자임)까지의 누적 비용을 저장한다. 3번 인덱스 값은 도시 3까지 가는 최소 비용이다.
# 우선순위 큐에 최소 비용을 0으로 한 출발 노드 삽입해서 while 시작.
# 출발 노드에서 갈 수 있는 도시와 비용을 탐색 -> heap에 다시 삽입
import sys
from heapq import *
input = sys.stdin.readline
N = int(input()) # 도시
M = int(input()) # 버스
graph = [[] for _ in range(N+1)] # 도시(인덱스)에서 도착지와 비용
# 버스 노선 입력 받고 graph에 담기
for _ in range(M):
a, b, cost = map(int, input().split())
graph[a].append([b, cost])
start, end = map(int, input().split()) # 목표 출발지와 도착지. 입력받기 끝
# 나머지 초기값 설정과 heap에서 쓸 처음 조건 삽입
costs = [1e9 for _ in range(N+1)] # 인덱스=도시번호=그 도시까지의 누적비용
heap = []
costs[start] = 0 # 시작지점 비용 0
heappush(heap, [0, start])
while heap:
current_cost, city = heappop(heap)
if costs[city] < current_cost: # costs에 최소값을 담을것이라 크다면 스킵
continue
# graph에 시작 도시로 갈 수 있는 도시들 for문 탐색
for next_city, next_cost in graph[city]:
sum_cost = next_cost + current_cost
if costs[next_city] <= sum_cost:
continue # costs에 담긴게 최소값일테니 크거나 같다면 필요없음
costs[next_city] = sum_cost
heappush(heap, [sum_cost, next_city])
print(costs[end]) # costs의 도착지 도시
# graph. 1번 인덱스: 1번 도시에서 [2,2] 2번 도시로 2 비용.
# [[2, 2], [3, 3], [4, 1], [5, 10]],
# [[4, 2]],
# [[4, 1], [5, 1]],
# [[5, 3]],