작성자 : 장아연
0. Recap
Deep Graph Encoder
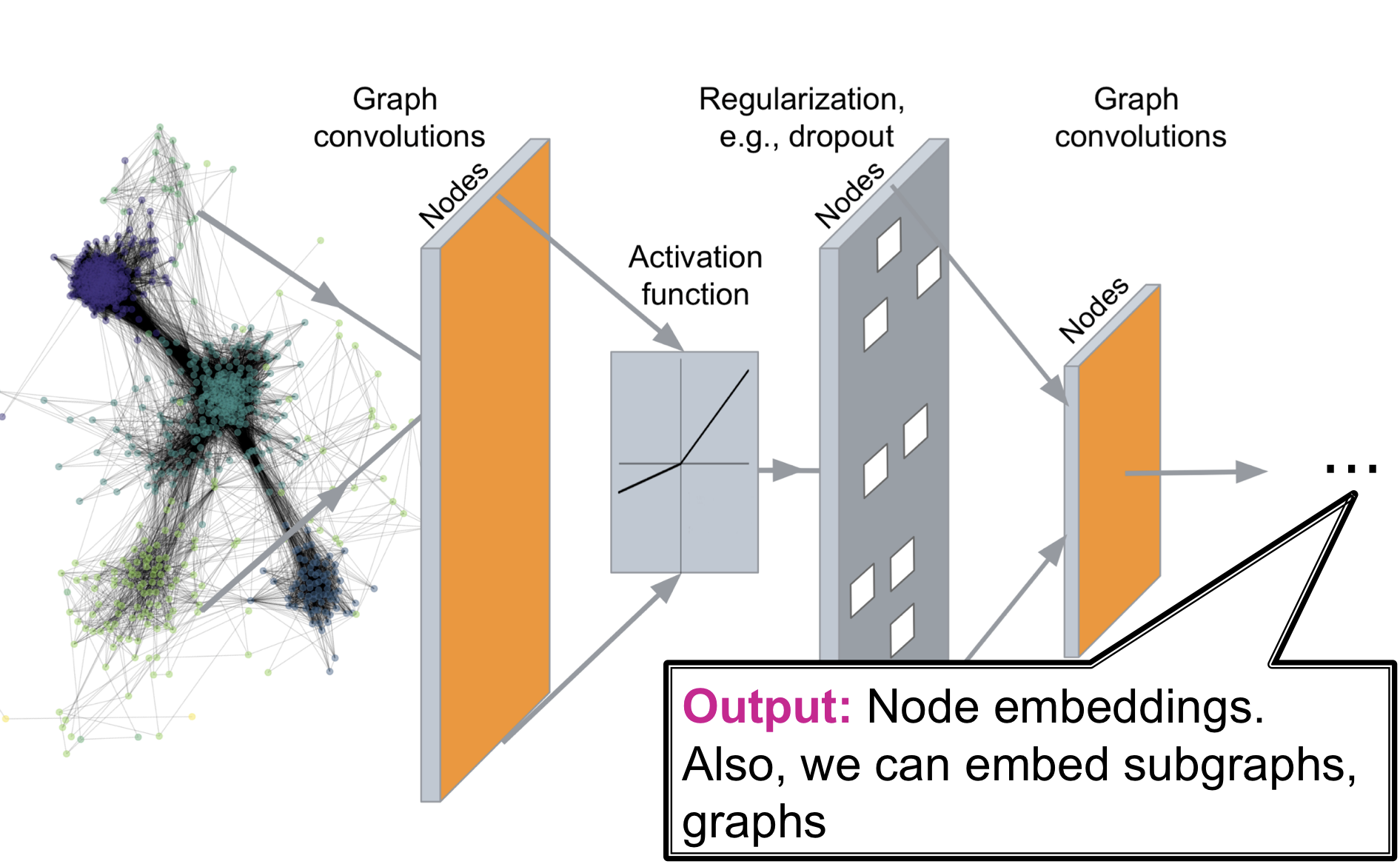
Deep Graph Encoders는 임의의 graph를 Deep Neural Network를 통과 시켜 embedding space로 사상 시키는 것
A General GNN Framework
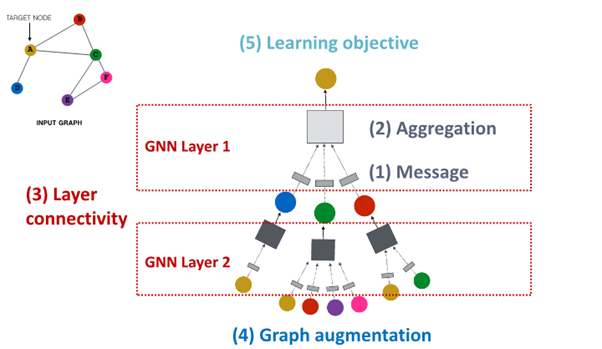
(4) Graph augmentation
: what kind of graph and feature augumentation can we create to shape the structure of this neural network
(5) Learning Objective
: learn objectives and how to make training work
1. Graph Augmentation for GNNs
Why Graph Augment
가정 : Raw input Graph 와 computational Graph는 동일
- Feature : lack features
- Graph Structure :
sparse -> inefficient passing
dense -> too costly passing
large -> not computational graph into GPU
즉, input graph는 embedding을 위한 computation graph의 적합한 상태가 아님.
Idea : Raw input Graph 와 computational Graph는 동일 X
Graph Augmentation Approaches
Graph Feature Augmentation
- lack features : feature augmentation을 통해 feature 생성
Standard Approach
필요성 : adj. matrix만 가지고 있는 경우 Input Graph에서 node feature가 없는 경우 흔히 발생
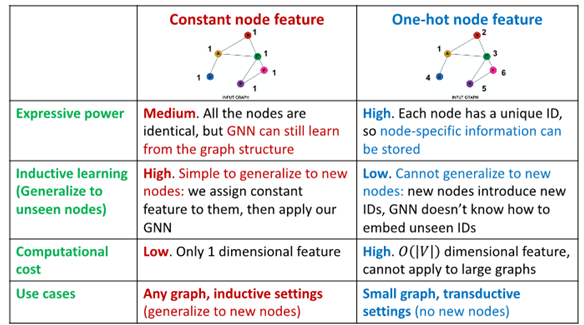
1. Constant Node Feature
Assign constant values to nodes
basically all the node have same future value of 1
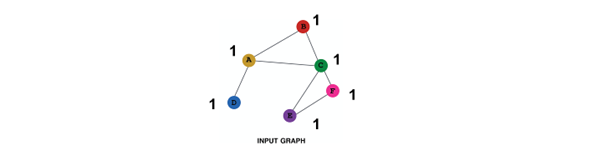
2. One-hot node feature
Assign unique IDs to nodes
IDs are converted to one-hot vectors
flag value 1 at ID of that single node

Constant Node Feature vs One-hot node feature
Cycle Count
필요성 : GNN 학습에 어려움을 겪는 특정 구조 존재
-
GNN은 이 속한 cycle의 길이 학습 불가
-
가 어떤 graph에 속해 있는지 구별 불가능
-
모든 node의 차수가 2임
-
computational graph는 같은 binary tree임
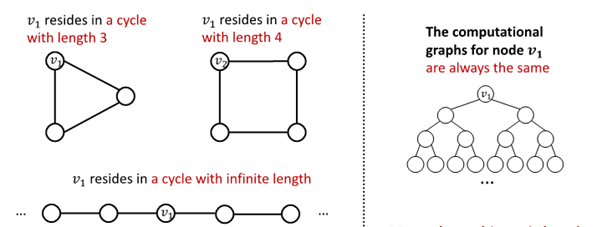
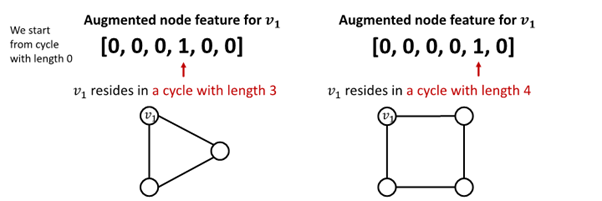
-
그 외 Node Degree, Clustering coeffiecient, PageRank, Centrality 등 이용
Graph Structure Augmentation
- too sparse : virtual node / edges를 생성
- too dense : message passing 과정에서 neighbors sampling
- too large : embedding 계산을 위해 subgraph sampling
Add Virtual Edge
개념
- virtual edge를 이용해 2-hop 관계의 이웃 노드 연결
- adj.matrix 대신 이용
예시
- Author(A)와 Author(B) 연결
: Author(A) -> paper -> Author(B)

Add Virtual node
개념
- virtual node를 이용해 graph의 모든 node를 연결
- 모든 node와 node는 distance 2를 가짐
: node(A) ->virtual node-> node(B)
예시
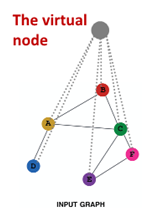
결과 : virtual node/edge 추가해 sparse한 graph에서 message passing 향상
Node Neighborhood Sampling
기존
- 모든 node는 message passing에 사용됨
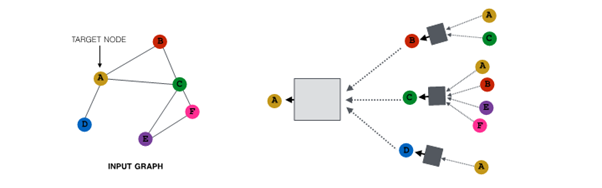
개념
- node neighborhood를 random sampling해 message passing 진행
예시 :
1. random하게 2개의 neighbor 선택해 sampling
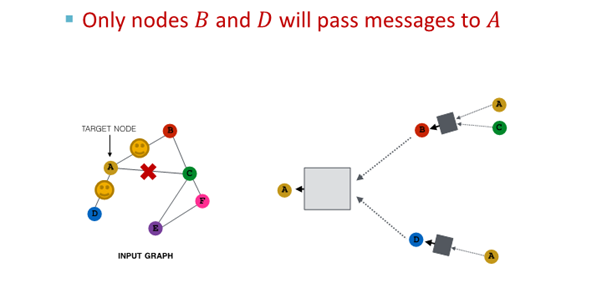
2. 다음 layer에서 다른 neighbor 선택해 resampling해 embedding 진행
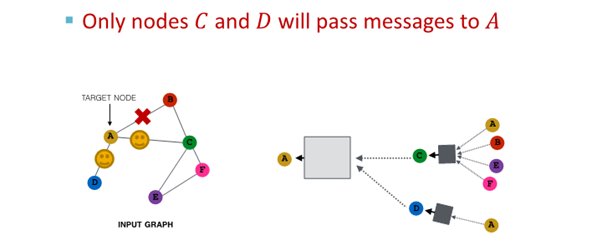
결과
- 모든 neighbor 사용한 경우와 유사한 embedding
- computational cost 경감
(large graph scaling 해줌)
2. Prediction with GNNs
How to train GNN?
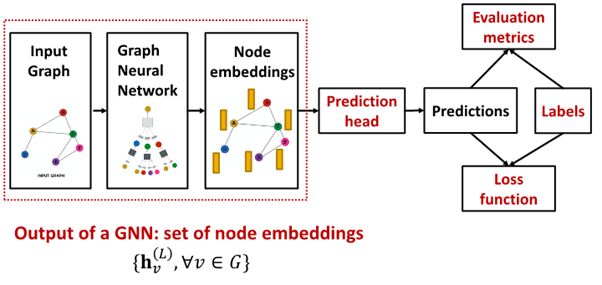
- : node L from graph neural network의 final layer
- Prediction head: final model's output
- Label : where label come from?
- Loss function : define loss function, what to optimize
Different Prediction Head
서로 다른 prediction head에 따라 서로 다른 task가 요구됨
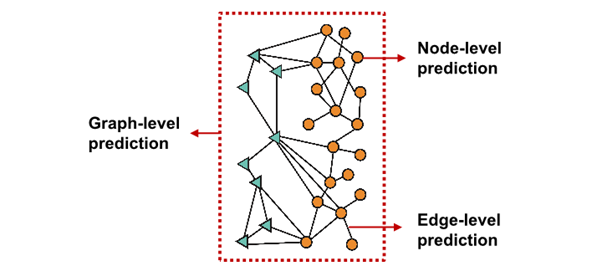
Node-level task
- node embedding 사용해 예측
- prediction head : { }
get -dim node embedding from GNN computation - way prediction의 경우
classification : classify among categories
regression : regress on target - ==
output head of given node=matrix time final embedding of node - : map node embedding from (embedding space) to (prediction)
Edge-level task
- node embedding pair 사용해 예측
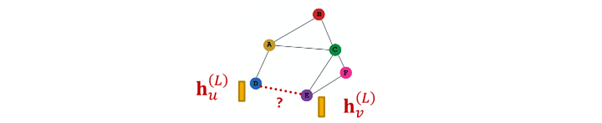
- -way prediction의 경우 : =
option for edge level prediction
1. Concatenation + Linear transformation

- =
- : 2d-dimensional => -dim embedding
2. Dot product
- =
- only applied to 1 way prediction (binary prediction)
- for -way prediction : multi-head attention과 유사
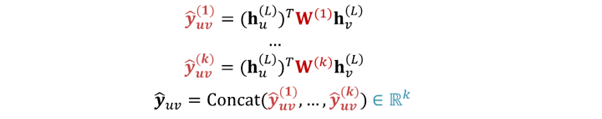
- trainable different matrix : ... 이용
=> every class get to learn its own transformation - prediction for every class인 ... 를 concat해 final prediction인 구함
Graph-level task
- graph 속 모든 node embedding 이용해 예측
- ={ }
take individual node embedding for every node and aggregate them to find embedding in graph
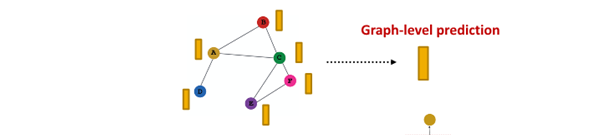
- 과 GNN에서 유사
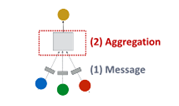
option for Graph level prediction
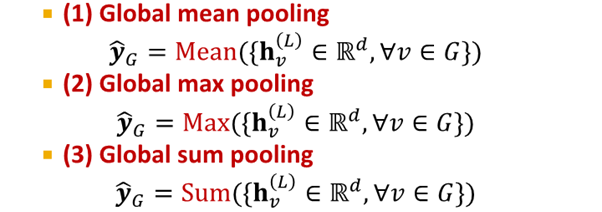
위 3개는 small graph에 적합함
large graph를 global pooling하여 information lose

- solution :
Hierarchical Global Pooling
Hierarchical Global Pooling
- 모든 node embedding을 위계 따라 aggregate
개념 예시

DiffPool idea : Hierarchically pool node embedding
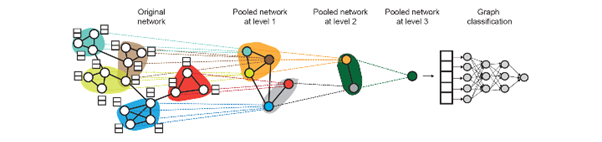
3. Training Graph Neural Network
4. Setting - up GNN Prediction Tasks
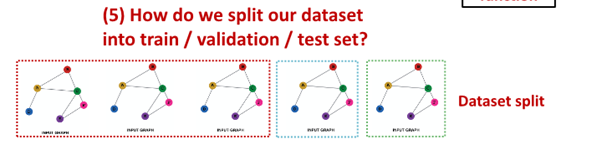
Fixed split vs Random split
Fixed split
- Train : GNN parameters를 optimize에 사용
- Validation : model/hyperparameters를 develope
- Test : final performance를 report하는 데 사용
-> test 결과에 대한 해당 실행 결과 보장X
Random split - randomly split training / validation / test dataset
-> 서로 다른 random seed에 대해 performance를 average함
Why Splitting Graph is special
image data splite하는 경우
- image classification은 모든 data point가 image로 각각의 data가 서로 independent함
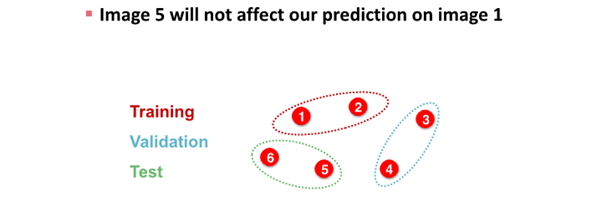
graph data splite하는 경우
- node classification은 모든 data point가 node로 각각의 data가 서로 dependent함
- node 1과 node 2는 node 5를 예측하는데 영향을 줌
: node 1과 node2가 train data, node 5가 test data인 경우, information leakage 발생 가능
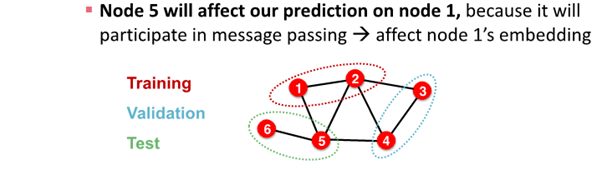
solution
1. Transductive setting
- entire graph in all dataset
- only split label
- dataset consist of one graph
- node / edge prediction
- train : entire graph, use node 1 & 2 label
- validation : entire graph, use node 3 & 4 label

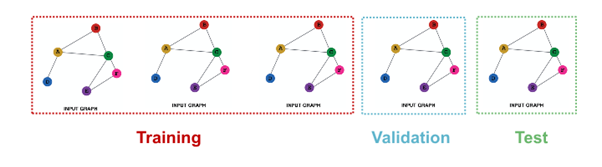
2. Inductive setting
- different graph in each dataset
- dataset consist of multiple graph
- generalize to unseen graph
- node / edge / graph task
- train : embedding 계산 graph over node 1 & 2, train use node 1 & 2 label
- validation : embedding 계산 graph over node 3 & 4, evaluate node 3 & 4 label

Example
1. Node Classification
- transductive node classification

- inductive node classification

- Graph Classification
- only in inductive setting
- test on unseen graph
- Link Classification
- predict missing edge
- unsupervised / self-supervised task
-> create label & dataset split
= we hide edge & let GNN predict whether edge exist

Setting up Link Prediction
1-0. Assign edge as Message edges or Supervision edges
- Message edges : GNN message passing에 사용
- Supervision edges : objectives 계산에 사용
1-1.
message edges : remain in graph
supervision edges : supervise edge prediction made by model
2-0. split edges as train / validation / test
2-1. Inductive link prediction split의 경우
- contain independent graph in dataset
- 각 dataset에는
message edges와supervision edges가 포함됨 supervision edgesnot fed in GNN
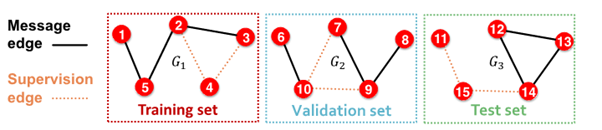
2-2. Transductive link prediction split의 경우- after train,
supervision edgesknown to GNN - use
supervision edgesat validation time
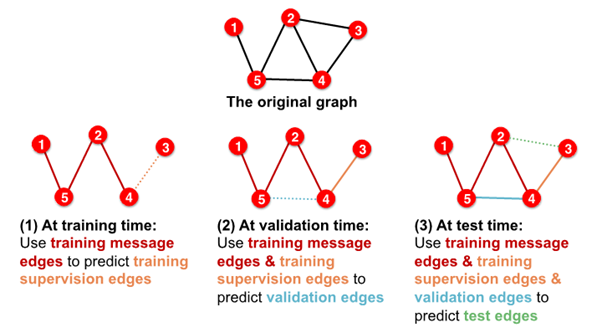
- in sum, 4 types of edges