1. 트리
트리(Tree)란?
- 데이터 간의 계층적 관계를 나타내기 위한 비선형 자료구조
: 트리의 핵심은 계층적 관계의 표현이며, 데이터 저장/삭제는 이를 위한 수단
트리 관련 용어 정리
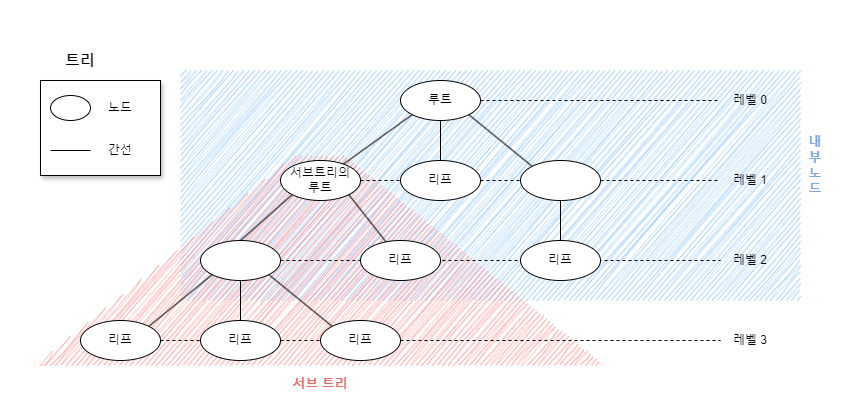
트리 구성 요소 관련
노드(Node)
- 트리에서 데이터가 저장되는 부분
간선(Edge)
- 노드와 노드를 연결하는 연결선
루트 노드(Root Node)
- 트리 구조의 최상단에 위치하여 부모 노드가 존재하지 않는 노드
- 1개의 트리에서 오직 1개만 존재
리프 노드(Leaf Node) / 단말 노드(Terminal Node)
- 트리 구조의 최하단에 위치한 노드로, 그 아래로 또다른 노드가 연결되어 있지 않은 노드
내부 노드(Internal Node) / 비단말 노드(Non-Terminal Node)
- 트리 구조에서 자식 노드가 존재하는 모든 노드
- 루트 노드를 포함한, 리프 노드 이외의 노드
노드/트리 간 관계 관련
부모(parent)
- 한 노드에서 간선으로 연결된 위쪽 노드
- 루트 노드를 제외한 모든 노드는 항상 1개의 부모 노드를 보유
자식(child)
- 한 노드에서 간선으로 연결된 아래쪽 노드
- 내부 노드는 여러 개의 자식 노드 보유 가능
형제(sibling)
- 동일한 부모 노드를 갖는 노드
조상(ancestor)
- 한 노드에서 간선을 통해 연결된 모든 위쪽 노드
- 트리 구조에서 루트 노드는 모든 노드들의 조상
자손(descendant)
- 한 노드에서 간선을 통해 연결된 모든 아래쪽 노드
기타 트리 관련 용어 정리
레벨(level)
- 트리 구조 내 한 노드와 루트 노드 간의 거리
- 루트의 레벨은 0
- 루트로부터 아래로 간선이 1개씩 전개될 때마다 레벨은 1씩 증가
차수(degree)
- 노드가 갖는 자식의 수
- n진 트리 : 모든 노드의 차수가 n 이하인 트리
ex) 모든 노드의 자식 수가 2개 이하 = 이진 트리높이(height)
- 루트로부터 가장 멀리 떨어진 리프까지의 거리(= 리프 레벨의 최댓값)
서브 트리(subtree)
- 트리 구조 내 한 노드를 루트로 정하고 그 자손들로 구성된 트리
널 트리(null tree)
- 노드, 간선이 존재하지 않는 트리
순서 트리(ordered tree) / 무순서 트리(unordered tree)
- 형제 노드 간 순서의 유무에 따라 구분
: 형제 노드 간 순서를 매기면 순서 트리, 순서를 매기지 않으면 무순서 트리
2. 이진 탐색 트리
이진 트리(Binary Tree)란?
- 모든 노드의 자식 수가 2개 이하인 트리
: 공집합 노드 또한 노드로 인정하기 때문- 루트 노드와 왼쪽 서브트리, 오른쪽 서브트리로 구성
아래의 트리들은 모두 이진 트리이며, 이들은 포화 이진 트리도, 완전 이진 트리도 아니다.
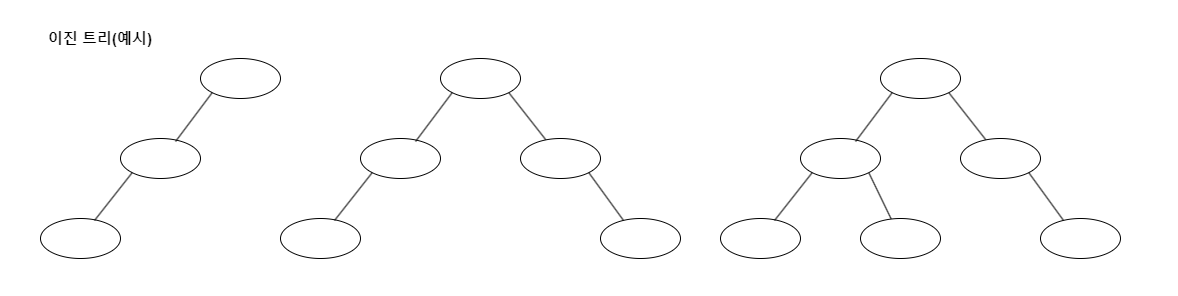
특별한 이진 트리
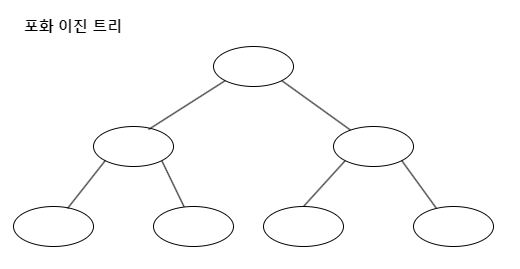
포화 이진 트리(Full Binary Tree)
- 각 레벨마다 개의 노드가 존재하고,
모든 내부 노드가 항상 2개의 자식 노드를 갖는 이진 트리
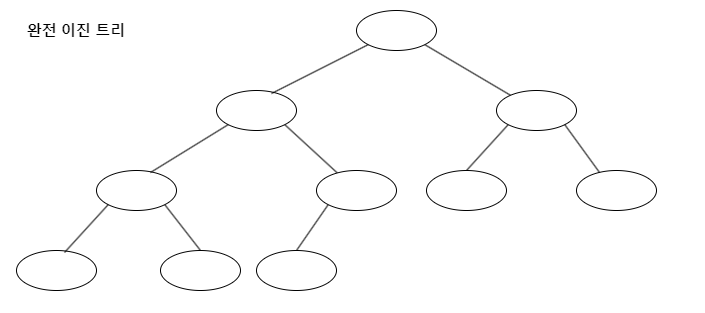
완전 이진 트리(Complete Binary Tree)
- 마지막 레벨을 제외한 각 레벨에 개의 노드가 존재하고,
마지막 레벨에서는 리프노드들이 왼쪽부터 빠짐없이 채워진 트리- 포화 이진 트리는 항상 완전 이진 트리이지만,
완전 이진 트리는 포화 이진 트리가 아닐 수도 있음
(아래는 완전 이진 트리이지만 포화 이진 트리가 아닌 경우에 해당)
이진 탐색 트리
이진 탐색 트리 / 이진 검색 트리(Binary Search Tree) 개요
- 이진 트리에 데이터 저장 규칙을 부여한 트리 형태의 비선형 자료구조
- 중복된 값은 저장 불가능
- 노드의 추가/삭제에 많은 시간을 소요
: 노드를 순차적으로 저장하지 않기 때문- 범위검색과 정렬에 유리
이진 탐색 트리의 성립 조건
- 이진 탐색 트리의 노드에 저장된, 데이터 저장 규칙이 적용되는 값은 항상 유일
- 루트 노드의 왼쪽 서브 트리
: 주어진 데이터 저장 규칙상 항상 루트 노드보다 앞서는 노드- 루트 노드의 오른쪽 서브 트리
: 주어진 데이터 저장 규칙상 루트 노드보다 뒤처지는 노드- 루트 노드의 왼쪽, 오른쪽 서브트리 역시 이진 탐색 트리
(즉, 1~3의 규칙은 루트 노드의 양쪽 서브트리에 대해서도 재귀적으로 적용)
3. 이진 탐색 트리의 구현
이진 탐색 트리의 핵심 기능
BinarySearchTree 인터페이스
package datastructure.tree;
import java.util.function.Consumer;
public interface BinarySearchTree<E extends Comparable<E>> {
TreeNode<E> search(E value); // 트리에서 지정한 데이터를 탐색
void add(E value); // 트리에 지정한 데이터를 추가
TreeNode<E> remove(TreeNode<E> value); // 트리에서 지정한 노드를 삭제
void preorderTraverse(TreeNode<E> node, Consumer<TreeNode<E>> action); // 전위 순회
void inorderTraverse(TreeNode<E> node, Consumer<TreeNode<E>> action); // 중위 순회
void postorderTraverse(TreeNode<E> node, Consumer<TreeNode<E>> action); // 후위 순회
boolean isEmpty(); // 빈 트리인지 확인
void dump(); // 트리에 저장된 데이터를 오름차순으로 출력
void clear(); // 트리의 모든 노드를 삭제
int getSize(); // 트리에 저장된 노드의 개수 반환
}저장 규칙을 따로 설정하지 않은 경우에는 이진 탐색 트리에 저장되는 데이터 타입에서의 비교 연산을 자동으로 적용하도록 제너릭 타입 E가 Comparable을 상속받게 했다.
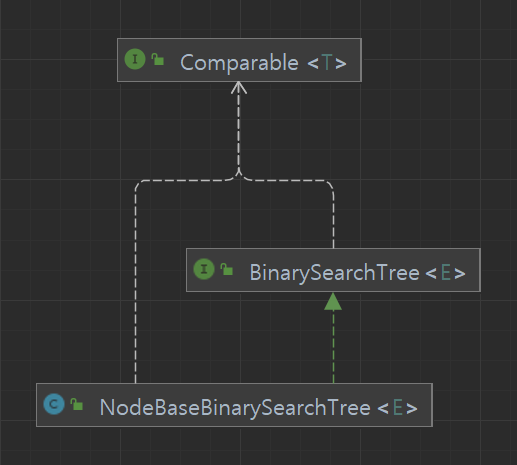
이진 탐색 트리 구현
- 전체 구현 코드는 여기를 참조
TreeNode 클래스
package datastructure.tree;
public class TreeNode<E extends Comparable<E>> {
private E data;
private TreeNode<E> left;
private TreeNode<E> right;
// 트리의 한 노드 생성
public TreeNode() {
this(null,null,null); // 루트 노드 삭제를 위한 더미 노드 생성에 활용
}
public TreeNode(E data) {
this(data, null, null); // 루트 노드 또는 리프 노드 생성 시 사용
}
public TreeNode(E data, TreeNode<E> left, TreeNode<E> right) {
this.data = data;
this.left = left;
this.right = right;
}
// 노드에 저장된 데이터 반환
public E getData() {
return data;
}
// 노드에 저장된 데이터 변경
public void setData(E data) {
this.data = data;
}
// 현재 노드의 왼쪽 자식 노드를 반환
public TreeNode<E> getLeftTree() {
return left;
}
// 현재 노드의 왼쪽 자식 노드를 변경
public void setLeftTree(TreeNode<E> left) {
this.left = left;
}
// 현재 노드의 오른쪽 자식 노드를 반환
public TreeNode<E> getRightTree() {
return right;
}
// 현재 노드의 오른쪽 자식 노드를 변경
public void setRightTree(TreeNode<E> right) {
this.right = right;
}
}NodeBaseBinaryTree 클래스
package datastructure.tree;
import java.util.Comparator;
import java.util.function.Consumer;
public class NodeBaseBinarySearchTree<E extends Comparable<E>> implements BinarySearchTree<E> {
private TreeNode<E> root; // 이진 검색 트리의 루트 노드를 가리키는 변수
private Comparator<? super E> comparator; // 이진 검색 트리의 데이터 저장 규칙
private int size; // 이진 검색 트리에 저장된 노드의 개수
// 이진 검색 트리 생성 시 데이터 저장 규칙 미설정
public NodeBaseBinarySearchTree() {
root = null;
comparator = null;
size = 0;
}
// 이진 검색 트리 생성 시 별도의 데이터 저장 규칙 설정
public NodeBaseBinarySearchTree(Comparator<? super E> comparator) {
this();
this.comparator = comparator;
}
// 루트 노드 반환
public TreeNode<E> getRoot() {
return root;
}
// 데이터 저장 규칙에 따른 비교 연산 수행
// 별도로 설정한 저장 규칙이 없으면 오름차순/사전순으로 저장
private int compare(E value1, E value2) {
return comparator == null ? value1.compareTo(value2) : comparator.compare(value1, value2);
}
// 지정한 값을 갖는 노드 탐색
@Override
public TreeNode<E> search(E value) {
// 1. 탐색 시작점은 루트 노드
TreeNode<E> node = root;
while (node != null) {
// 2. 찾으려는 데이터와 현재 노드의 데이터를 비교
switch (compare(value, node.getData())) {
case 0:
// 3-1. 현재 노드의 데이터가 찾으려는 데이터와 일치하면 현재 노드를 반환
return node;
case 1:
// 3-2. 규칙상 찾으려는 데이터가 현재 데이터보다 늦을 경우 오른쪽 자식 노드를 탐색
node = node.getRightTree();
break;
case -1:
// 3-3. 규칙상 찾으려는 데이터가 현재 노드의 데이터보다 앞설 경우 왼쪽 자식 노드를 탐색
node = node.getLeftTree();
break;
}
}
// 트리 내에 찾는 데이터가 없는 경우
return null;
}
// 이진 탐색 트리에 이미 노드가 존재할 때의 데이터 추가 동작
private void addNode(TreeNode<E> current, E value) {
// 1. 현재 노드의 데이터와 저장하려는 데이터를 비교
switch (compare(value, current.getData())) {
case -1:
// 2-1. 규칙상 저장할 데이터가 현재 노드의 데이터보다 앞설 경우
// 3-1. 현재 노드의 왼쪽 자식 노드 추가
if (current.getLeftTree() == null) {
current.setLeftTree(new TreeNode<>(value));
// 4-1. 저장된 노드의 개수 1 증가
size++;
} else {
// 이미 저장된 노드가 있으면 빈 자리를 발견할 때까지 재귀
addNode(current.getLeftTree(), value);
}
break;
case 0:
// 2-2. 이미 트리에 저장된 데이터인 경우 그대로 종료
return;
case 1:
// 2-3. 규칙상 저장할 데이터가 현재 노드의 데이터보다 늦을 경우
// 3-3. 현재 노드의 오른쪽 자식 노드 추가
if (current.getRightTree() == null) {
current.setRightTree(new TreeNode<>(value));
// 4-3. 트리의 노드 개수 1 증가
size++;
} else {
addNode(current.getRightTree(), value);
}
break;
}
}
@Override
public void add(E value) {
if (isEmpty()) {
// 빈 트리일 경우 루트 노드 추가 후 트리의 노드 개수 1 증가
root = new TreeNode<>(value, null, null);
size++;
} else {
addNode(root, value);
}
}
// 삭제할 리프 노드가 왼쪽 자식 노드일 때의 삭제 처리
private TreeNode<E> removeLeftLeaf(TreeNode<E> leafParent) {
if (leafParent != null) {
// 1. 삭제할 리프 노드는 별도로 저장
TreeNode<E> deleted = leafParent.getLeftTree();
// 2. 리프 노드 삭제
leafParent.setLeftTree(null);
// 3. 삭제된 리프 노드 반환
return deleted;
}
// 삭제할 노드가 존재하지 않음
return null;
}
// 삭제할 노드가 오른쪽 자식 노드일 때의 삭제 처리 (removeLeftLeaf와 동일한 방식)
private TreeNode<E> removeRightLeaf(TreeNode<E> parent) {
if (parent != null) {
TreeNode<E> deleted = parent.getRightTree();
parent.setRightTree(null);
return deleted;
}
return null;
}
@Override
public TreeNode<E> remove(TreeNode<E> target) {
TreeNode<E> virtualRoot = new TreeNode<>(); // 루트 노드의 삭제를 수행하기 위한 더미 노드
TreeNode<E> parent = virtualRoot; // 현재 노드의 부모 노드
TreeNode<E> current = root; // 현재 노드
TreeNode<E> deleted; // 삭제할 노드
// 루트 삭제를 원활히 수행하기 위한 사전 작업
virtualRoot.setRightTree(root);
// 삭제할 노드 탐색
while (current != null) {
// 1. 삭제할 노드의 데이터와 현재 노드의 데이터를 비교
int cond = compare(target.getData(), current.getData());
// 2-1. 삭제할 노드 도달 시 탐색 종료
if (cond == 0) {
break;
}
// 2-2. 삭제할 노드가 아닐 경우 부모 노드를 현재 노드로 갱신
parent = current;
// 3-2. 비교 결과에 따라 다음 탐색 노드 선택
current = (cond < 0) ? current.getLeftTree() : current.getRightTree();
}
// 삭제할 노드가 존재하지 않는 경우 그대로 종료
if (current == null) {
return null;
}
// 삭제할 노드가 리프 노드인 경우
if (current.getLeftTree() == null && current.getRightTree() == null) {
if (parent.getLeftTree() == target) {
// 현재 부모 노드의 왼쪽 자식 노드가 삭제할 노드
deleted = removeLeftLeaf(parent);
} else {
// 현재 부모 노드의 오른쪽 자식 노드가 삭제할 노드
deleted = removeRightLeaf(parent);
}
}
// 삭제할 노드의 자식 노드가 1개인 경우
else if (current.getLeftTree() == null || current.getRightTree() == null) {
// 1. 현재 노드의 자식 노드를 찾고, 삭제할 노드는 별도로 저장
TreeNode<E> child = current.getLeftTree() != null ? current.getLeftTree() : current.getRightTree();
deleted = current;
// 2. 현재 노드의 부모 노드와 1.에서 찾은 자식 노드를 직접 연결하여 트리에서 현재 노드 삭제
if (parent.getLeftTree() == deleted) {
parent.setLeftTree(child);
} else {
parent.setRightTree(child);
}
}
// 삭제할 노드의 자식 노드가 2개인 경우(루트 노드의 삭제도 수행하는 분기)
else {
TreeNode<E> replaced = current.getRightTree(); // 대체할 노드
TreeNode<E> replacedParent = current; // 대체할 노드의 부모 노드(시작은 삭제할 노드)
// 1. 삭제 대상을 대체할 노드를 탐색
// (삭제할 대상의 오른쪽 서브트리 중 저장 규칙상 가장 앞서는 노드)
while (replaced.getLeftTree() != null) {
replacedParent = replaced;
replaced = replaced.getLeftTree();
}
// 2. 삭제 대상의 데이터는 백업
E tempValue = current.getData();
// 3. 삭제할 노드의 데이터는 대체할 노드의 데이터로 변경
// (덮어쓰기를 통해 트리에서 트리 내 삭제 대상의 데이터 제거)
current.setData(replaced.getData());
// 4. 대체할 노드의 부모 노드에 오른쪽 자식 노드를 직접 연결
// (연결 관계를 조정하여 삭제 대상을 대체한 노드를 트리에서 분리)
if (replacedParent.getLeftTree() == replaced) {
replacedParent.setLeftTree(replaced.getRightTree()); // 대체한 노드가 왼쪽 자식 노드였던 경우
} else {
replacedParent.setRightTree(replaced.getRightTree());
}
// 5. 백업해둔 삭제 노드 복원
deleted = replaced;
deleted.setData(tempValue);
}
// 루트 노드가 삭제된 경우 루트 노드를 갱신
if (virtualRoot.getRightTree() != root) {
root = virtualRoot.getRightTree();
}
// 이진 검색 트리에 저장된 노드의 개수 1 감소 후 삭제된 노드 반환
size--;
return deleted;
}
... (코드 중략)
// 빈 이진탐색트리인지 확인
@Override
public boolean isEmpty() {
return root == null;
}
// 이진 탐색 트리에 저장된 데이터를 모두 삭제
@Override
public void clear() {
System.out.println("Try clearing...");
postorderTraverse(root, this::remove);
System.out.println("Clearing complete!!\n");
}
// 이진 탐색 트리에 저장된 노드의 개수 반환
@Override
public int getSize() {
return size;
}
// 이진 탐색 트리에 저장된 데이터를 오름차순으로 출력
@Override
public void dump() {
if (isEmpty()) {
System.out.println("Tree is empty!!");
return;
}
System.out.print("Result: ");
inorderTraverse(root, node -> System.out.print(node.getData() + " "));
System.out.println();
}
... (코드 생략)
}실행용 샘플 코드 및 실제 실행 결과
package datastructure.tree;
public class BinarySearchTreeMain {
public static void main(String[] args) {
NodeBaseBinarySearchTree<Integer> tree = new NodeBaseBinarySearchTree<>();
// 첫번째 테스트: 트리에 노드 추가 후 랜덤으로 데이터 삭제하기
System.out.println("Tree test 1:");
tree.add(6);
tree.add(1);
tree.add(3);
tree.add(8);
tree.add(4);
tree.add(7);
tree.add(9);
tree.add(5);
tree.add(2);
System.out.printf("Tree node count: %d\n", tree.getSize());
tree.printResult();
System.out.println();
System.out.println("Removing random node in tree:");
while (!tree.isEmpty()) {
// 1~9 사이 정수 중 임의의 값 1개를 선택하여 해당 값을 갖는 노드를 탐색
TreeNode<Integer> target = tree.search((int) (Math.random()*9+1));
// 이미 삭제된 노드면 재시도
if (target == null) {
continue;
}
// 트리에서 노드 삭제 후 삭제된 데이터, 삭제 후 트리 내 노드의 개수 출력
System.out.printf("Removed data: %d, Tree node count: %d\n",
tree.remove(target).getData(), tree.getSize());
// 데이터 삭제 후 트리 내 모든 데이터를 오름차순으로 출력
tree.dump();
}
System.out.println("\n");
// 두번째 테스트: 트리에 노드 추가 후
System.out.println("Tree test 2:");
tree.add(7);
tree.add(5);
tree.add(9);
tree.add(2);
tree.add(4);
tree.add(1);
tree.add(6);
tree.add(8);
tree.add(3);
// 트리에 저장된 노드 개수, 트리 내 모든 노드를 전위, 중위, 후위 순회한 결과를 출력
System.out.printf("Tree node count: %d\n", tree.getSize());
tree.printResult();
System.out.println();
// 트리 내 모든 데이터를 한번에 삭제 후 그 결과를 출력
tree.clear();
System.out.printf("Tree node count: %d\n", tree.getSize());
tree.dump();
}
}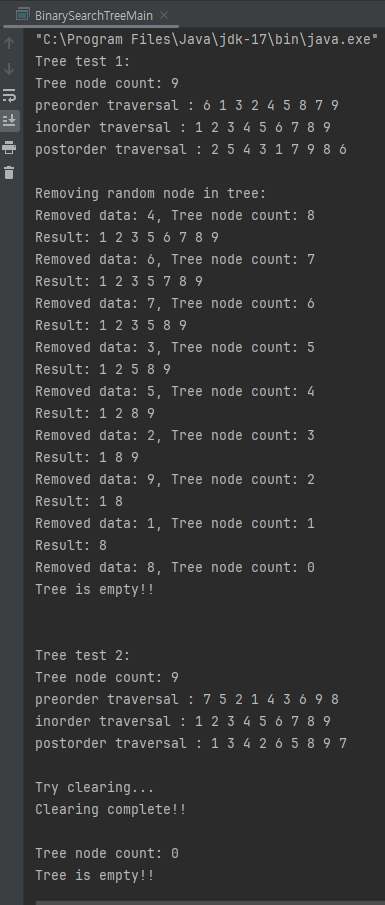
- 첫번째 테스트와 두번째 테스트에서 사용한 이진 트리는 각각 아래와 동일
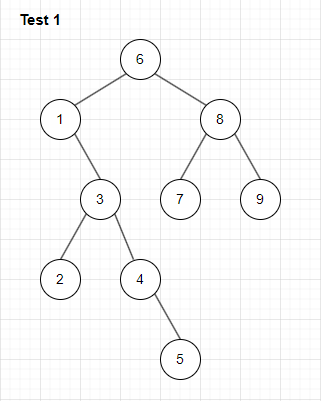
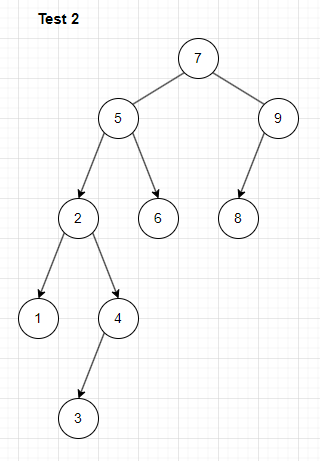
전위, 중위, 후위 순회
- 루트 노드 방문 시점을 기준으로 구분되며, 서브트리에 대해 재귀적으로 수행되는 순회
전위 순회(preorder traversal)
루트 노드 - 왼쪽 서브트리 - 오른쪽 서브트리순으로 순회하는 방식중위 순회(inorder traversal)
왼쪽 서브트리 - 루트 노드 - 오른쪽 서브트리순으로 순회하는 방식후위 순회(postorder traversal)
왼쪽 서브트리 - 오른쪽 서브트리 - 루트 노드순으로 순회하는 방식
NodeBaseBinaryTree 클래스 - 전위, 중위, 후위 순회 구현
- 현재 노드에서 수행할 동작을 별도로 지정할 수 있도록 함수형 인터페이스인
Consumer<TreeNode<E>>를 파라미터로 사용
public class NodeBaseBinarySearchTree<E extends Comparable<E>> implements BinarySearchTree<E> {
... (코드 생략)
@Override
public void preorderTraverse(TreeNode<E> node, Consumer<TreeNode<E>> action) {
if (node != null) {
// 전위 순회: 현재 노드 - 왼쪽 서브트리 - 오른쪽 서브트리 순으로 순회
action.accept(node); // 현재 노드에서는 지정한 동작 수행
preorderTraverse(node.getLeftTree(), action);
preorderTraverse(node.getRightTree(), action);
}
}
@Override
public void inorderTraverse(TreeNode<E> node, Consumer<TreeNode<E>> action) {
if (node != null) {
// 중위 순회: 왼쪽 서브트리 - 현재 노드 - 오른쪽 서브트리 순으로 순회(서브트리는 재귀적으로 순회)
inorderTraverse(node.getLeftTree(), action);
action.accept(node);
inorderTraverse(node.getRightTree(), action);
}
}
@Override
public void postorderTraverse(TreeNode<E> node, Consumer<TreeNode<E>> action) {
if (node != null) {
// 후위 순회: 왼쪽 서브트리 - 오른쪽 서브트리 - 현재 노드 순으로 순회(서브트리는 재귀적으로 순회)
postorderTraverse(node.getLeftTree(), action);
postorderTraverse(node.getRightTree(), action);
action.accept(node);
}
}
... (코드 생략)
}Reference
- Do-it! 자료구조와 함께 배우는 알고리즘 입문(Bohyoh Shibata 지음, 강민 옮김)
- 윤성우의 열혈 자료구조(윤성우 지음)
- 자바의 정석 3판(남궁성 지음)
