Sailors (sid, sname, rating, age)
Reserves (sid, bid, day, rname)
Sailors
- 40bytes per tuple
- 100 tuples/page
- 1000 pages
Reserves
- 50bytes per tuple
- 80 tuples/page
- 500 page
0. 기초
- 후술 할 join 연산 최적화를 다루기 전 기초DB의 관계 대수 연산자에 대해 간략히 오약
1) 관계 대수 (relational algebra) 연산자
: 릴레이션에 필요한 요구를 처리하는 연산자
① 일반 집합 연산자
: 합집합, 교집합, 차집합, 카티션 프로덕트
② 순수 관계 연산자
: 셀렉트 프로젝트, 조인, 디비전
2) 조인
- 다른 연산자는 생략하고 조인 연산 종류에 대해 알아보자
1. Equality Join(동일조인)
SELECT * FROM
Reserve R, Sailors S
WHERE R.sid = S.sid
R과S의 동일 조인 연산을 하기 위해 카티션 프로덕트(RXS)를 하게된다. 이는 매우 inefficient. 따라서 I/O cost를 고려해서 위 쿼리의 조인 연산을 어떻게 수행하면 좋을까?
M : # of R tuples
N : # of S tuples
pR : #of tuples/R-page
pS : # of tuples/S-page
하단의 내용은 개념보다 각 조인의 cost를 비교하여 (join) query evalutation을 수행하고자 한다.
1) Simple Nested Loop Join
R의 모든 튜플에 대해 S의 모든 튜플을 검사.
- cost : 1000 + 1000X100X500 = 501000 I/O
= M + pR x M x N
2) Page Oriented Nested Loop Join
① R is outter, S is inner
- cost : 1000pages + 1000 x 500pages
= M + M x N
② R is inner, S is outer
- cost : 500pages + 500 x 1000pages
= N + M x N
=> smaller relation(S) should be outer!!
3) Index Nested Loops Join
: index on join column of one Relation (S로 가정)
- cost = R page I/O +((M x pR) x S의 tuple을 찾는 비용)
① Hash : 약 1.2 cost for finding matching S tuples
i) S의 sid(PK)에 hash index 생성(as inner)
Outer relation(R) scan : 1000 I/O s
for each R tuples : 1.2 I/O(get data entry) + 1 I/O (get tuple)
=> total cost = 1000 + 1000 x 100 x (2.2) = 221000 I/O
ii) R의 sid(PK가 아님)에 hash index 생성(as inner)
Outer Relation(S) scan : 500 I/O
for each S tuples : 1.2 I/O (find index page with data) + ?(get tuples!-PK가 아니기 때문에 tuple이 다수 존재함)
그렇다면 S tuples를 읽어오기 위해 몇번의 I/O가 필요한가?
i. sid에 clustered index가 생성되어있고, S의 matching tuples가 한 페이지에 존재한다고 가정하면
- ADD 40000 I/O
ii. sid에 unclustered index가 생성되어 있다고 가정하면
- S의 matching tuples가 약2.5개 존재하므로(균등분포)
2.5 x 40000 = 100000 I/O
따라서 clustered index on sid of Reserves => 48500+40000
unclustered index on sid of Reserves => 48500 + 100000
=> unclustered index여도 simplex nested loop join 보다는 낫다
② B+ tree : 약 2~4 cost
4) Block Nested Loopsr Join
- #outer blocks = # of pages of outer / block size
- block size(1000page) 가정
i. outer(R) : 10x5000 = 5000I/O
ii. outer(S) : 5x1000 = 5000I/O
5) Sort-Merge Join
: R과 S를 조인속성에 대해 각각 정렬 후 병합
R을 100page씩 10개의 내부 정렬(1)을 한 후 10개의 run을 병합(2)
=> 2단계에 걸치며, 각 단계별 모든 page를 READ/WRITE
=> cost = 1000 x 2 x 2 = 4000 I/O
S를 100page씩 5개의 내부 정렬(2)을 한 후 5개의 run을 병합(2)
=> 2단계에 걸치며, 각 단계별 모든 page를 READ/WRITE
=> cost = 500 x 2 x 2 = 2000 I/O
R과 S를 병합하면서 각 릴레이션의 모든 page scan
=> cost = 500 + 1000
∴ cost = 7500 I/O
6) Refinement of Sort-Merge Join
=> 4500 I/O로 줄일 수 있다. 어떻게?
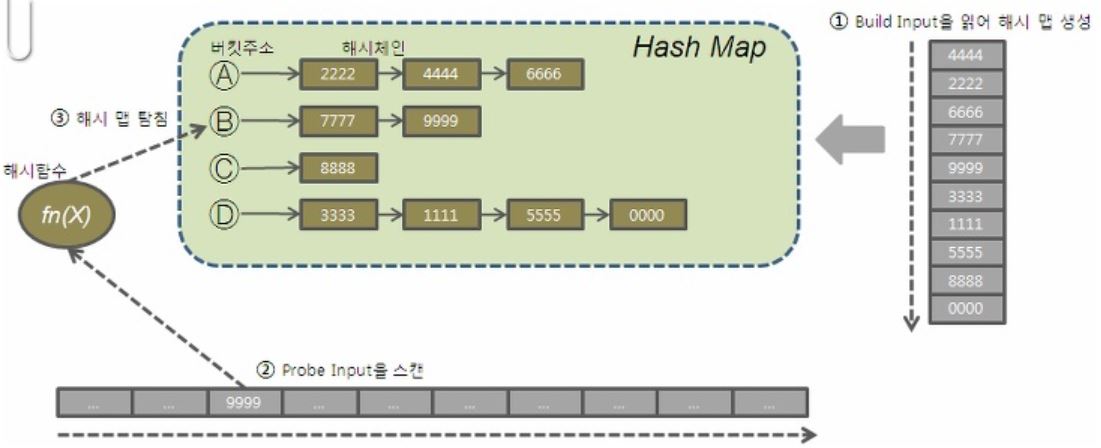
7) Hash-Join
: 두 테이블 중 한 테이블(Build Input, Driving Table)을 조인키를 기반으로 메모리에 해시테이블을 생성하고 해시테이블 내에 행들을 위치시키기 위해 해시함수를 사용하고 나머지 테이블을 스캔하면서 조인조건을 만족하는 레코드를 찾는 조인방법
① Build Input : driving table, 둘 중 더 작은 릴레이션
② Probe Input : 나머지 릴레이션
-
S릴레이션(둘 중 더 작은 릴레이션)을 읽어 Hash Area에 해시 테이블을 생성한다. (해시 함수에서 리턴 받은 버킷 주소로 찾아가 해시 체인에 엔트리를 연결)
-
R릴레이션(Probe Input)을 읽어 해시 테이블을 탐색하면서 JOIN 한다.
-
해시 함수에서 리턴 받은 버킷 주소로 찾아가 해시 체인을 스캔하면서 데이터를 찾는다.