1. Background

1.1 Oridinary Differential Equations(ODE)

Neural ODE 논문을 이해하기 위해서는 ODE에 대한 약간의 배경지식이 필요하다. ODE는 만약 공학수학 수업을 들었다면 한번씩 공부해 보았을 가능성이 높다. 한국말로 하면 상미분방정식이다. 즉, 여러 미분방정식의 형태 중 하나라는 것이다. 미분방정식이란 어떠한 상태를 표현하는 함수 $f$와 함수의 미분값 $f'$사이의 관계를 표현하는 방정식이다. 이 때 함수 $f$가 독립변수 1개에 대한 함수라면, 상미분 방정식이고 2개 이상이면 편미분 방정식 이라고 부른다. 이러한 미분방정식은 세상을 이해하는데 많은 도움을 주는 방정식이다(온 세상이 미방이다). 한 가지 예시로 들면, 뉴턴역학에서 중요한 변수가 바로 중력가속도 인데, 사실은 위치함수를 두번 미분한 함수이자, 속도함수를 한번 미분한 함수의 형태이기에, 세상이 움직이는 다양한 형태를 미분방정식 형태로 표현할 수 있는 것 이다.

그렇다면 미분방정식을 통해서 얻고자 하는게 무엇일까? 바로 독립변수에 따라 상태를 표현하는 함수 $f$를 구하는 것이다! 이러한 ODE를 기반으로 새로운 Neural Network 프레임워크를 제안한 것이 바로 Neural ODE 이다. 간단한 ODE 수식을 살펴보면서 ODE의 특징을 알아보자.

1.1.1 ODE example

아래의 식은 초기조건이 주어지고, ODE이 주어졌을 때 적분을 통해 풀어나가는 간단한 예시이다. 하지만 대부분의 미분방정식이 이렇게 깔끔한 해석해를 얻을 수 없다.

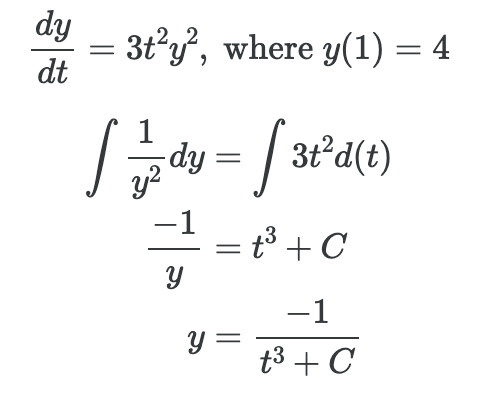
이렇게 각각의 독립변수 t, y에 대해서 적분을 진행하게 되면 y를 얻게 된다. 이후 처음에 얻었던 초기조건을 활용해서 C의 값을 얻을 수 있다.

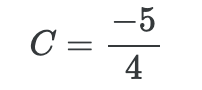
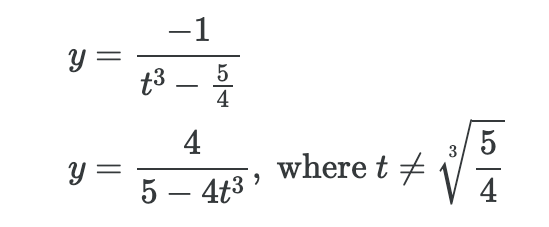
2. Neural ODE

2.1 What is Neural ODE

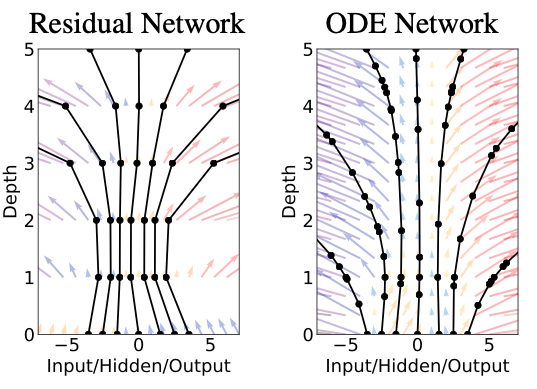
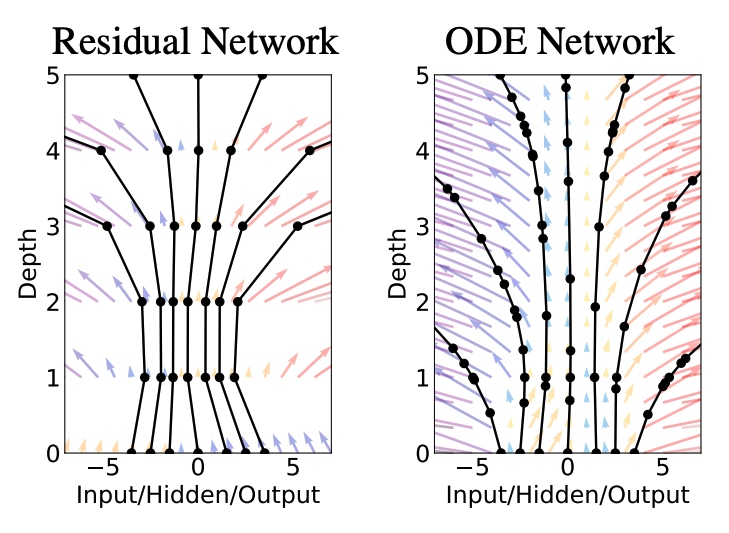
Neural ODE의 정의는 비교적 간단하다. 기존의 RNN 혹은 Resnet 그리고 normalizing flow들의 구조를 살펴보면 다음과 같은 수식으로 정리할 수 있다.

여기서 $h_t$는 $t$단계의 layer를 통과한 latent vector를 의미한다. 즉 아래의 Resnet 그림에서 weight layer를 통과한 $F(x)$가 Neural ODE 수식에서 $f$를 뜻한다.

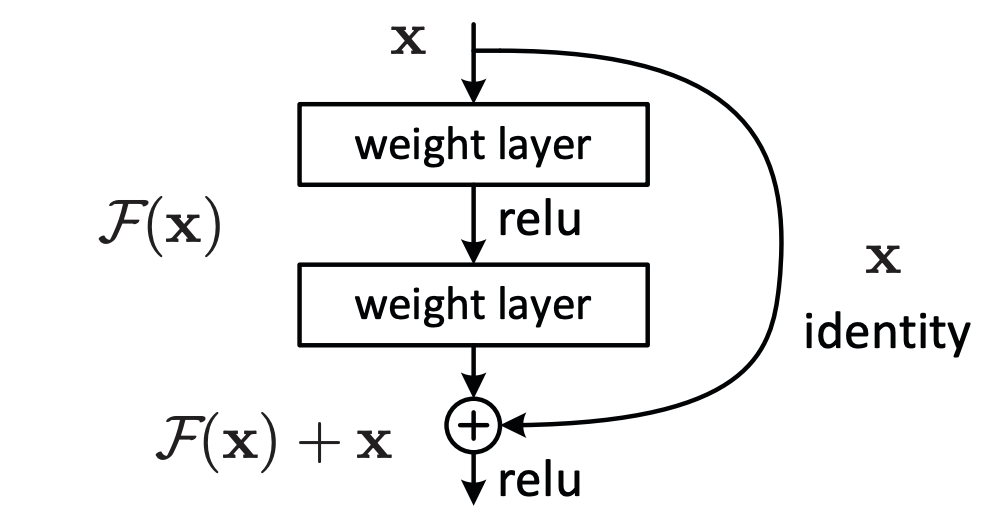
이러한 Resnet 공식을 오일러 기법을 활용해서 잘게 쪼갠다면, 아래와 같이 표현할 수 있다.

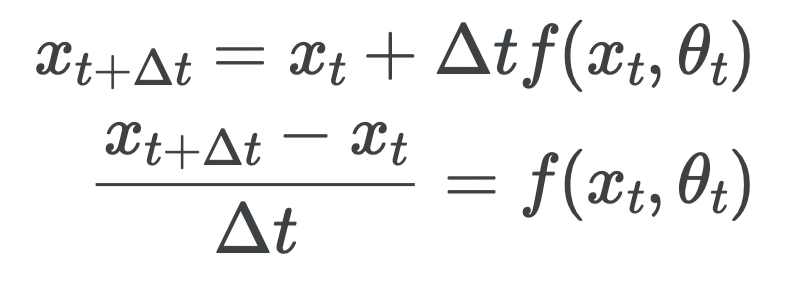
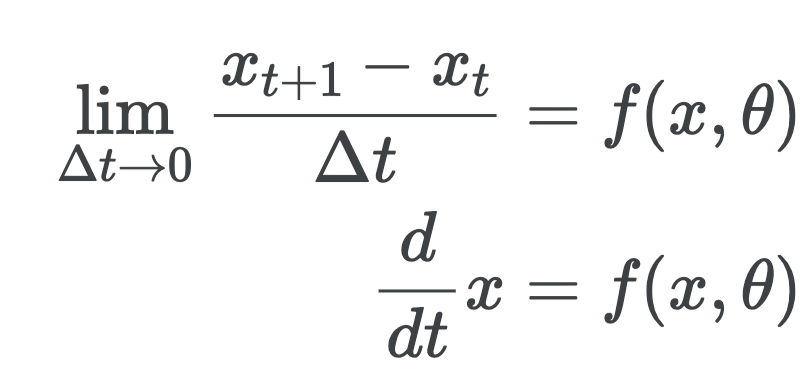
이를 다시 쓰면, 다음과 같다.

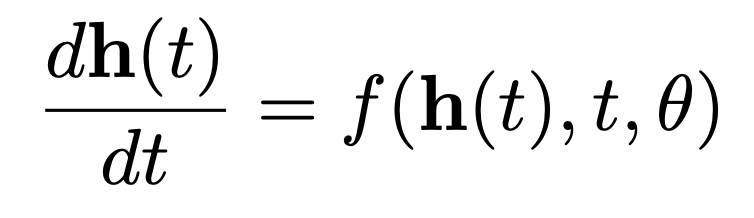
2.2 Neural ODE solver

즉, Neural ODE에서 Neural Network의 output은 바로 현재 상태의 미분값이 된다. 이러한 개념을 이용한다면 다음 상태값을 얻을 수 있다. 간단하게 생각하면, 현재위치 에서의 미분값을 적분하여, 얼만큼 이동할 것인지 정한 뒤, 초기값에 더해준다면, 다음상태에서의 위치를 알 수 있는 것 이다. 이를 수식으로 표현하면 다음과 같다.

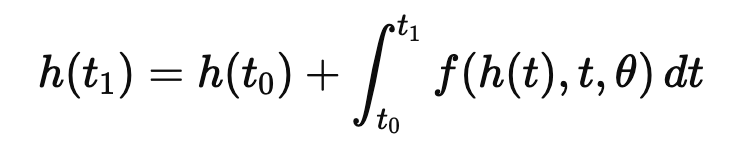
이렇게 다음 상태의 값을 얻도록 해주는 것이 바로 ODE solver이다. ODE solver는 저 Neural Network의 결과값을 적분하여, 최종 상태 $h(t_1)$을 얻어내도록 해주는 도구이다.

그렇다면 이 Neural ODE는 어떻게 학습할 수 있을까? 바로 저 최종상태 $h(t1_1)$에 대해서 loss를 계산하여 학습을 진행한다. 즉 최종 결과값을 토대로 진행된 모든 ODE solver 내의 네트워크가 학습하게 되는 구조이다.

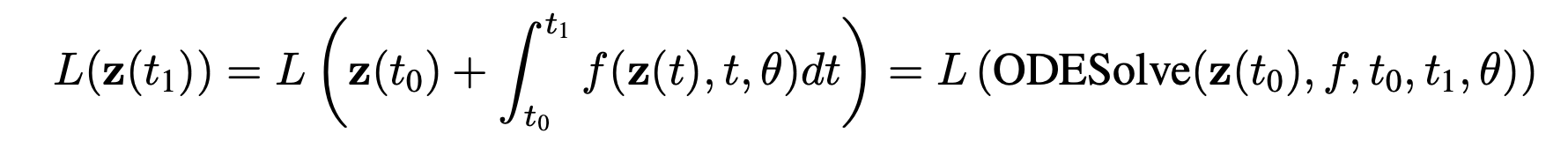
2.3 Backpropagation

위에서 말한 것 처럼 저렇게 최종 상태의 오차를 기반으로 학습을 진행해도 된다. 하지만 이러한 방법은 ODE solver내의 모든 파라미터를 저장해야 하므로 메모리 비용이 매우 크다. 따라서 본 논문에서는 adjoint sensitivity method를 사용하여 이를 해결하였다.

위의 그림과 같이 만약 adjoint sensitivity method를 사용하지 않는다면, 하나의 Loss를 통해 모든 state가 업데이트되는 형식이고, 이러면 각각의 state에서 진행된 모든 ode solver의 파라미터를 저장해야 한다는 단점이 있다. 이런 걸 해결하기 위해, loss를 각 구간별로 나누어, 각 스텝에서의 오차 반영률을 계산하여 각각 업데이트를 진행하는 형태이다. 이러한 과정을 수식으로 표현하면 다음과 같다.

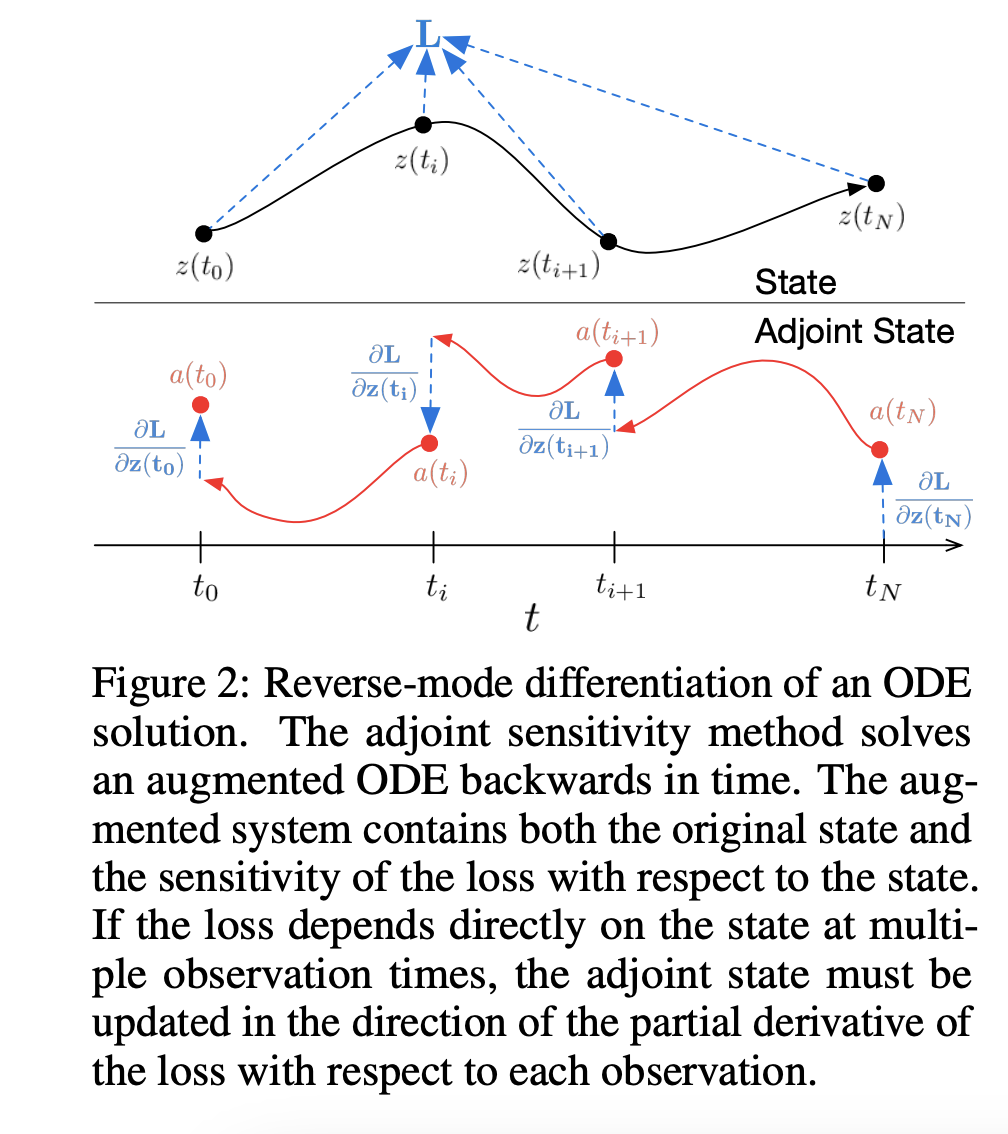
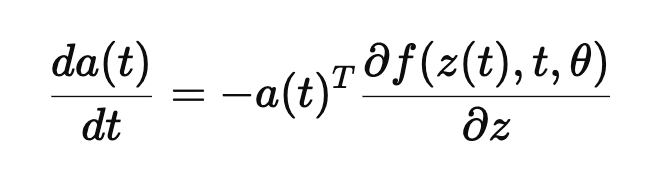
$a(t)$ 는 adjoint라고 불리며, 이는 시간 𝑡 에서 손실 𝐿에 대한 상태 𝑧(𝑡)의 기여도를 나타낸다. 즉 수식을 해석하면Loss의 변화율이 𝑓의 변화율에 의해 결정된다는 사실을 보여준다. 이렇게 각각의 상태에서의 기여도를 반영하여 backpropagation을 진행하여 메모리 문제를 해결하였다.

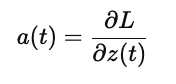
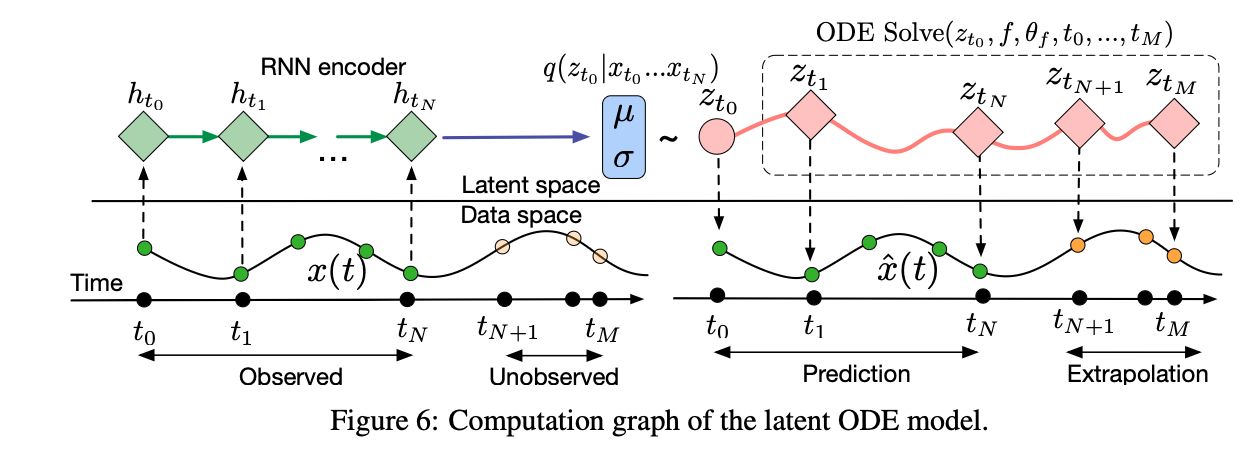
3. Results

Neural ODE는 시간을 연속적으로 모델링하므로, 불규칙한 시간 간격으로 샘플링된 spirals (나선형 데이터)를 reconstruction 하고 예측하는 성능이 뛰어나다. 아래의 그림들 통해 확인할 수 있듯이, RNN 기반 모델은 고정된 시간 간격 또는 단순한 보간 방식을 사용하기에, 불규칙한 시간 간격의 데이터 처리에 한계가 있을 수 있음을 확인할 수 있다.

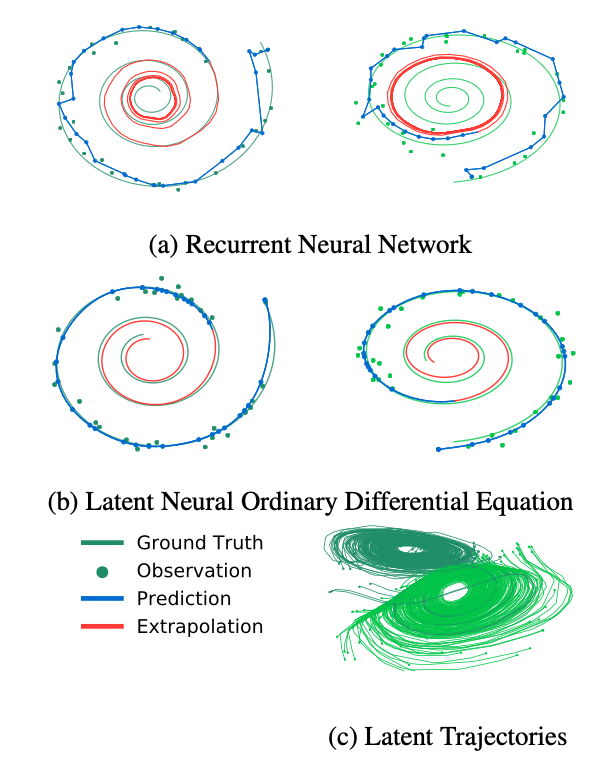
이렇게 Neural ODE가 예측과 Reconstruction을 잘하는 이유는 아래의 그림에서 직관적으로 확인할 수 있다.