[Do it 딥러닝 입문] 05장

H_jiwoo·2022년 3월 28일

딥러닝 공부

목록 보기

5/6

테스트 세트로 모델 튜닝하기

로지스틱 회귀로 모델 훈련하고 평가하기

cancer 데이터 세트를 읽어 들여 훈련 세트와 테스트 세트로 나누기

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
x = cancer.data
y = cancer.target
x_train_all, x_test, y_train_all, y_test = train_test_split(x,y,stratify=y, test_size=0.2,random_state=42)

fit() 메서드에 x_train_all, y_train_all을 전달해 모델 훈련 → score() 메서드에 x_test, y_test를 전달해 성능 평가

from sklearn.linear_model import SGDClassifier
sgd = SGDClassifier(loss='log', random_state=42)    #손실함수 : 로지스틱 손실 함수
sgd.fit(x_train_all, y_train_all)
sgd.score(x_test, y_test)

0.8333333333333334

모델 튜닝하기

: SGDClassifier 클래스의 다른 매개변수들을 바꿔 모델의 성능을 높이는 것

loss 매개변수를 log에서 hinge로 바꾸기 → 선형 서포트 벡터 머신(SVM: 훈련 데이터의 클래스를 구분하는 경계선을 찾는 작업)문제를 푸는 모델이 만들어짐

from sklearn.linear_model import SGDClassifier
sgd = SGDClassifier(loss='hinge', random_state=42)
sgd.fit(x_train_all, y_train_all)
sgd.score(x_test, y_test)

0.9385964912280702 → 로지스틱 회귀로 만든 모델보다 성능이 좋아짐

그러나 테스트 세트로 모델을 튜닝하면 실전에서 같은 성능을 기대하기 어려움, 모델의 일반화 성능이 왜곡됨 → ‘테스트 세트의 정보가 모델에 새어나감’

검증 세트 사용

테스트 세트는 모델 튜닝 후 실전에 투입하기 전 한 번만 사용하고, 훈련 세트를 조금 뗴어 검증 세트를 만들어 사용하는 것이 좋음

#데이터 세트 준비 
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
x = cancer.data
y = cancer.target
x_train_all, x_test, y_train_all, y_test = train_test_split(x,y,stratify=y, test_size=0.2,random_state=42)

#검증 세트 분할 -> 앞서 전체 데이터 세트를 훈련 세트:테스트 세트=8:2로 나누고, 훈련 세트를 훈련세트:검증 세트=8:2로 다시 나눔
x_train, x_val, y_train, y_val = train_test_split(x_train_all, y_train_all, stratify=y_train_all, test_size=0.2, random_state=42)
print(len(x_train),len(x_val))  #훈련 세트와 검증 세트 분할 비율 출력

364 91 → 455개의 훈련 세트가 훈련 세트(x_train) 364개, 검증 세트 (x_val) 91개로 나뉨

검증 세트로 모델 평가하기

from sklearn.linear_model import SGDClassifier
sgd = SGDClassifier(loss='log', random_state=42)
sgd.fit(x_train, y_train)
sgd.score(x_val, y_val)

0.6923076923076923

데이터 전처리 : 스케일 조정하기

특성의 스케일이 다른 경우, 잘 정리된 데이터도 전처리를 해야 함
경사하강법은 스케일에 민감한 알고리즘 → 특성의 스케일을 맞추는 등의 전처리를 해야 함

1. 스케일 조정하지 않고 훈련하기

위스콘신 유방암 데이터와 단일층 신경망 모델을 사용

#박스 플롯으로 두 특성의 스케일 확인하기
print(cancer.feature_names[[2,3]])
plt.boxplot(x_train[:,2:4])
plt.xlabel('feature')
plt.ylabel('value')
plt.show()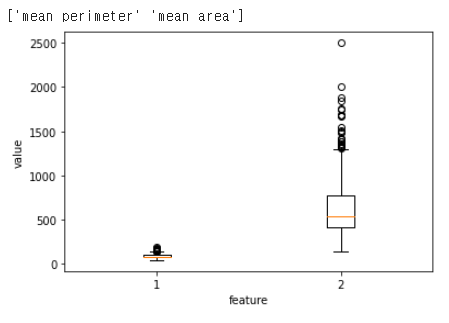

⇒ mean perimeter는 주로 100~200사이에, .mean area는 주로 200~2000사이에 값들이 집중되어 있음

4장의 SingleLayer 클래스 변형

class SingleLayer:
  def __init__(self,learning_rate=0.1):
    #1.__init__() 메서드 작성
    self.w = None   
    self.b = None 
    self.losses=[]    #손실함수의 결과값을 저장할 리스트. 샘플마다 손실 함수를 계산하고 그 결괏값을 모두 더해 샘플 개수로 나눈 평균값을 저장 
    self.w_history =[]    #가중치를 기록할 변수 
    self.lr = learning_rate   #학습률 파라미터 -> 가중치의 업데이트 양을 조절 => 적절한 학습률을 이용해 손실 함수의 표면을 천천히 이동하며 전역 최솟값을 찾음

  #2.정방향 계산
  def forpass(self,x):
    z = np.sum(x*self.w)+self.b   
    return z

  #3.역방향 계산
  def backprop(self,x,err):
    w_grad = x*err   
    b_grad = 1*err    
    return w_grad, b_grad
  
  def add_bias(self,x):
    return np.c_[np.ones((x.shpae[0],1)),x]   #행렬의 맨 앞에 1로 채워진 열 벡터를 추가
    
  #5.activation()메서드 구현;시그모이드 계산 
  def activation(self,z):
    a = 1/(1+np.exp(-z))
    return a
      
  #6.훈련을 위한 fit()메서드 구현
  def fit(self, x, y, epochs=100):
    self.w = np.ones(x.shape[1])    
    self.b = 0   
    self.w_history.append(self.w.copy())  #w_history에 가중치 기록 
																					#넘파이 배열을 리스트에 추가하면 실제 값 복사가 아닌 배열 참조 -> 가중치 변수 self.w의 값이 바뀔 떄마다 그 값을 복사해 w_history에 추가해야 함
    np.random.seed(42)
    for i in range(epochs):
      loss = 0
      indexes = np.random.permutation(np.arange(len(x)))  #인덱스 섞기
      for i in indexes:   #모든 샘플에 대해 반복
        z = self.forpass(x[i])   #정방향 계산
        a = self.activation(z)   #활성화 함수 적용 
        err = -(y[i]-a)     #오차 계산
        w_grad, b_grad = self.backprop(x[i],err)    #역방향 계산   
        self.w -= self.lr*w_grad    #학습률을 적용해 가중치 업데이트
        self.b -= b_grad   #절편 업데이트
				#가중치 기록
        self.w_history.append(self.w.copy())
        #안전한 로그 계산을 위해 클리핑한 후 손실을 누적
        a = np.clip(a, 1e-10, 1-1e-10)    #np.clip() : 주어진 범위 밖의 값을 범위 양 끝의 값으로 잘라냄
        loss +=-(y[i]*np.log(a)+(1-y[i])*np.log(1-a))
      self.losses.append(loss/len(y))   #에포크마다 평균 손실 저장

  #7.에측하는 메서드 구현
  def predict(self,x):
    z = [self.forpass(x_i) for x_i in x]   
    return np.array(z) > 0   

  #8.정확도 계산을 위한 score()메서드 구현
  def score(self,x,y):
    return np.mean(self.predict(x)==y)

#모델 훈련하고 평가하기
layer1 = SingleLayer()
layer1.fit(x_train, y_train)
layer1.score(x_val,y_val)

0.9120879120879121 → 정확도 약 91%

#가중치 확인하기
w2=[]
w3=[]
for w in layer1.w_history:
  w2.append(w[2])
  w3.append(w[3])
plt.plot(w2,w3)
plt.plot(w2[-1],w3[-1],'ro')
plt.xlabel('w[2]')
plt.ylabel('w[3]')
plt.show()

mean perimeter에 비해 mean area의 스케일이 커 w3 값이 학습 과정에서 큰 폭으로 흔들리며 변화, w2는 0부터 시작하여 조금씩 최적값에 가까워짐

⇒ w3에 대한 그레디언트가 크기 때문에 w3 축을 따라 가중치가 크게 요동치고 있다

: 가중치의 최적값에 도달하는 동안 w3 값이 크게 요동치므로 모델이 불안정하게 수렴

→ 스케일 조정!

2. 스케일을 조정해 모델 훈련

표준화
- 신경망에서 자주 사용하는 스케일 조정 방법 중 하나
- 특성값에서 평균을 빼고 표준편차로 나누기
- 평균이 0이고 분산이 1인 특성이 만들어짐
- 사이킷런의 StandardScaler 클래스로 표준화 할 수있음

#1.넘파이로 표준화 구현하기
train_mean = np.mean(x_train,axis=0)
train_std = np.std(x_train,axis=0)    #mean()과 srd()함수의 axis 매개변수를 0으로 지정하면 2차원 배열의 열을 기준으로 통계치를 계산해 하나의 행 벡터로 반환
x_train_scaled=(x_train-train_mean)/train_std    #훈련 세트 x_train에서 평균을 빼고 표준편차로 나눔

#2.모델 훈련하기
layer2=SingleLayer()
layer2.fit(x_train_scaled,y_train)
w2=[]
w3=[]
for w in layer2.w_history:
  w2.append(w[2])
  w3.append(w[3])
plt.plot(w2,w3)
plt.plot(w2[-1],w3[-1],'ro')
plt.xlabel('w[2]')
plt.ylabel('w[3]')
plt.show()

w2와 w3의 변화 비율이 비슷 → 대각선 방향으로 가중치 이동
두 특성의 스케일을 비슷하게 맞춤 → 최적값에 빠르게 접근

#성능 평가
layer2.score(x_val,y_val)

0.37362637362637363 → 정확도 약 37%

⇒ 모델은 훈련 세트와 검증 세트의 스케일이 비슷할 것으로 기대했으나, 검증 세트의 스케일은 바꾸지 않아 성능이 좋지 않음 → 검증 세트도 표준화 전처리

val_mean = np.mean(x_val,axis=0)
val_std = np.std(x_val,axis=0)
x_val_scaled = (x_val-val_mean)/val_std
layer2.score(x_val_scaled,y_val)

0.967032967032967 → 정확도 약 97%

x_val_scaled = (x_val - train_mean) / train_std
plt.plot(x_train_scaled[:50,0],x_train_scaled[:50,1],'bo')
plt.plot(x_val_scaled[:50,0],x_val_scaled[:50,1],'ro')
plt.xlabel('feature1')
plt.ylabel('feature2')
plt.legend(['train set','val.set'])
plt.show()

훈련 세트의 평균, 표준 편차를 사용해 검증 세트를 변환 → 검증 세트와 훈련 세트를 동일한 비율로 변환시키기

과대적합과 과소적합

과대적합

모델이 훈련 세트에서는 좋은 성능을 내지만 검증 세트에서는 낮은 성능을 내는 경우
훈련 세트와 검증 세트에서 측정한 성능의 간격이 큼 → ‘분산이 크다’
훈련 세트에 충분히 다양한 패턴의 샘플이 포함되지 않음 경우 과대적합이 발생할 수 있음 → 더 많은 훈련 샘플을 모아 검증 세트의 성능을 향상시킬 수 있음
훈련 샘플을 더 많이 모을 수 없는 경우 모델이 훈련 세트에 집착하지 않도록 가중치를 제한 → ‘모델의 복잡도를 낮춘다’

과소적합

모델이 훈련 세트와 검증 세트에서 비슷한 성능을 내지만 두 성능 모두 낮은 경우
훈련 세트와 검증 세트에서의 성능이 점점 가까워지지만, 성능 자체가 낮음 → ‘편향이 크다’
모델이 충분히 복잡하지 않아 훈련 데이터에 있는 패턴을 모두 잡아내지 못하는 현상 → 복잡도가 더 높은 모델을 사용하거나 가중치의 규제 완화

학습 곡선(에포크-손실함수 그래프)과 과대/과소적합

훈련 세트의 손실은 에포크가 진행될수록 감소 / 검증 세트의 손실은 에포크 횟수가 최적점을 지나면 오히려 상승 → 과대적합되기 시작 (최적점 이후에도 계속해서 훈련 세트로 모델을 훈련시키면 모델이 훈련 세트의 샘플에 더 밀착하여 학습하기 때문)
최적점 이전에는 훈련 세트와 검증 세트의 손실이 비슷한 간격을 유지하면서 함께 줄어듬 → 이 영역에서 학습을 중지시키면 과소적합된 모델이 만들어짐

모델 복잡도-손실 함수 그래프와 과대/과소적합

모델 복잡도 : 모델이 가진 학습 가능한 가중치 개수. 층의 개수나 유닛의 개수가 많아지면 복잡도가 높은 모델이 만들어짐
모델이 복잡해지면 무조건 좋은것은 X, 과대적합의 경우

편향-분산 트레이드오프

과소적합된 모델(편향)과 과대적합된 모델(분산)사이의 관계
편향과 분산이 반비례 관계
적절한 편향-분산 트레이드오프를 선택했다 : 분산이나 편향이 너무 커지지 않도록 적절한 중간 지점을 선택하는 것

가중치 규제

가중치의 값이 커지지 않도록 제한하는 기법
가중치를 규제하면 모델의 일반화 성능이 올라감
그래프로 모델의 성능을 평가할 때
- 경사가 완만한 그래프가 박스로 표시한 샘플 데이터를 더 잘 표시 → 경사가 완만한 그래프가 급한 그래프에 비해 성능이 좋다고 평가
- 샘플 데이터에 딱 맞는 그래프 : 모델이 몇 개의 데이터에 집착해 새로운 데이터에 적응하지 못함, 좋은 성능을 가진 것이 아님 → ‘모델이 일반화되지 않았다’ ⇒ 규제를 사용해 가중치를 제한하면 모델이 몇 개의 데이터에만 집착하지 않아 일반화 성능을 높일 수 있음
데이터셋에서 볼 수 있는 일반적인 패턴이 아니라 기존 학습에 큰 영향을 끼칠 수 있는 데이터를 제한할 때 사용

L1 규제

손실함수에 L1 노름norm (전체 가중치 각각의 절댓값의 합)을 더한것
- L1 노름 : (n: 가중치의 개수)
- L1 노름에 규제의 양을 조절하는 하이퍼파라미터 α를 곱해 손실함수에 더함
  
  - 규제가 약해짐 : α값이 작으면 w의 합이 커져도 손실함수의 값이 큰 폭으로 커지지 않음
  - 규제가 강해짐 : α값이 크면 전체 손실 함수의 값이 커지지 않도록 w값의 합이 작아져야함

L1 규제를 적용한 손실 함수의 도함수에 학습률을 곱해 가중치 업데이트 (sign(w) : w의 부호)
L1 규제를 추가한 로지스틱 손실 함수를 경사하강법으로 최적화 → 규제 하이퍼파라미터 a와 가중치의 부호의 곱을 더해 업데이트 할 그레디언트에 더해주기
```
w_grad+=alpha*np.sign(w)  #alpha:규제 하이퍼파라미터
```
절편은 복잡도에는 영향을 주지 않음 → 절편에 대해 규제 X
SGDClassifier 클래스의 penalty 매개변수 값을 l1으로 지정해 L1 규제 적용 가능
라쏘(Lasso) 모델 : 회귀 모델에 L1규제를 추가한 것
- 일부 가중치를 0으로 만들 수 있음 → 가중치를 0인 특성=모델에서 사용할 수 없음 → 사용할 특성을 선택하는 효과를 얻을 수 있음
L1 규제는 하이퍼파라미터 α에 많이 의존 → 가중치의 크기에 따라 양이 변하지 않으므로 규제 효과가 좋다고 할 수 없음
가중치의 크기에 상관없이 상수값을 빼 불필요한 가중치의 수치를 0으로 만듬 → 중요한 가중치만 취함 ⇒ 특성을 제외하는 효과는 있지만 모델의 복잡도가 떨어짐

L2 규제

손실 함수에 가중치에 대한 L2 노름norm의 제곱을 더함
- L2 노름 :
L2 노름의 제곱에 규제의 양을 조절하는 하이퍼파라미터 α를 곱해 손실함수에 더함
L2 규제를 추가한 로지스틱 손실 함수를 경사하강법으로 최적화 → 규제 하이퍼파라미터 a와 가중치의 곱을 더해 업데이트 할 그레디언트에 더해주기
```
w_grad+=alpha*w
```
L2 규제는 그레디언트 계산에 가중치 값 자체가 포함되므로 가중치의 부호만 사용하는 L1 규제보다 더 효과적
가중치를 완전히 0으로 만들지 않음
특히 선형 모델의 일반화에 사용하기 좋음
릿지(Ridge) 모델 : 회귀 모델에 L2 규제를 적용한 것
- 사이킷런에서 sklearn.linear_model.Ridge 클래스로 제공, SGDClassifier 클래스에서는 penalty 매개변수를 l2로 지정해 L2 규제 추가 가능. 두 클래스 모두 규제의 강도는 alpha 매개변수로 제어