역전파 고수가 되어보자

김회정·2023년 7월 12일
0

머신러닝

목록 보기
4/7

이 글에 등장하는 예시와 jupyter notebook은 Andrej Karpathy의 Building makemore Part 4: Becoming a Backprop Ninja을 참고해 작성했습니다.

1. 배경

PyTorch 및 TensorFlow와 같은 라이브러리는 자동 미분 엔진을 제공하고 있다. 이러한 편리성 때문에 관련된 지식이 없더라도 딥러닝 모델을 설계하고 훈련하는 것이 매우 편리해졌다. 그럼에도 불구하고 편리함 뒤에 감춰진 복잡한 과정을 한번 살펴보는 것은 딥러닝 보다 깊게 이해하는데 도움이 될 수 있을 것이다. (근데 이게 도움이 되는지 솔직히 잘 모르겠네요 ㅎ)

따라서 이번 포스트에서는 간단한 신경망을 만들고 예측값에 대한 손실값의 그래디언트를 직접 구해보고자 한다. 직접 계산한 그래디언트는 PyTorch의 자동 미분 엔진을 통해 구한 그래디언트의 값과 비교해 검증한다.

2. 모델 구조

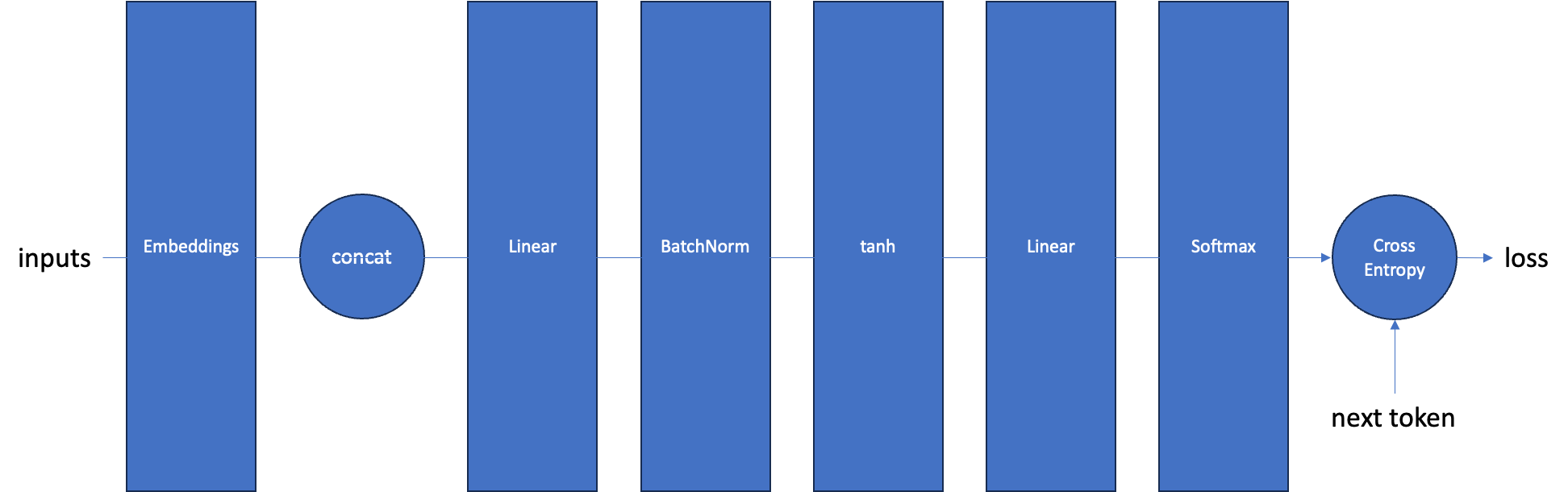
본 포스트에서 만들 신경망은 매우 간단한 형태의 언어 모델(Language Model)이다. 해당 모델의 순전파 과정은 다음과 같다.

  1. 토큰의 시퀸스를 임베딩을 통해 벡터로 변환한다.
  2. 변환된 각 토큰의 벡터를 이어붙여 하나로 만든다.
  3. 이어붙인 벡터를 순방향 신경망(Linear)을 통과시킨다.
  4. batch normalization을 적용한다.
  5. 활성화 함수(tanh)를 적용한다.
  6. 활성화 함수를 적용한 값을 두번째 순방향 신경망을 통과시켜 어휘 사이즈의 벡터로 변환한다.
  7. softmax를 적용하고 cross entropy 손실을 구한다.

해당 과정을 그림으로 표현하면 다음과 같다.

3. 설정

다음과 같은 설정을 사용한다

  • 베치 사이즈: 32
  • 어휘 사이즈(vocabulary size): 10,000
  • 시퀸스 길이: 4
  • 임베딩 차원: 10
  • 은닉층(hidden layer) 차원: 64
  • seed: 2147483647

해당 설정을 이용해서 다음과 같이 랜덤한 데이터를 생성할 수 있다. 생성한 데이터를 통해 손실을 구하고 역전파를 수행할 것이다. 

batch_size =32 # 배치 사이즈 
n = batch_size # 편의상 n이란 변수로 배치 사이즈를 치환한다
vocab_size = 10000 # 어휘 사이즈
seq_len = 4 # 시퀸스 길이
n_embd = 10 # 임베딩 차원
n_hidden = 64 # 은닉층 차원
g = torch.Generator().manual_seed(2147483647) # 결과 재현을 위한 장치

# 랜덤 데이터 생성
x_batch = torch.randint(0, vocab_size, (batch_size, seq_len), generator=g)
y_batch = torch.randint(0, vocab_size, (batch_size, ), generator=g)

4. 모델 가중치

모델의 가중치는 다음과 같다. 손수 생성한 가중치를 이용해 순전파를 진행한다.

# 임베딩
C  = torch.randn((vocab_size, n_embd), generator=g)
# 첫번째 레이어 가중치 (weight)
W1 = torch.randn((n_embd * seq_len, n_hidden), generator=g) * 0.1
# 첫번째 레이어 편향 (bias)
b1 = torch.randn(n_hidden, generator=g) * 0.1 
# 두번째 레이어 가중치
W2 = torch.randn((n_hidden, vocab_size), generator=g) * 0.1
# 두번째 레이어 편향
b2 = torch.randn(vocab_size, generator=g) * 0.1
# BatchNorm 레이어 가중치
bngain = torch.randn((1, n_hidden))*0.1 + 1.0
# BatchNorm 레이어 편향
bnbias = torch.randn((1, n_hidden))*0.1

parameters = [C, W1, b1, W2, b2, bngain, bnbias]
print(sum(p.nelement() for p in parameters)) # 총 파라미터의 수 (752,752)
for p in parameters:
  p.requires_grad = True

5. 순전파

앞서 만든 가중치와 랜덤 데이터를 이용해 순전파하는 과정은 다음과 같다.
B는 배치 사이즈를 의미하고, S는 시퀸스 길이, E는 임베딩 사이즈, H는 은닉층 사이즈, 마지막으로 V는 어휘 사이즈를 의미한다.

앞서 언급한 순전파 절차에 따른 코드는 다음과 같다.

  1. 토큰의 시퀸스를 임베딩을 통해 벡터로 변환한다.
emb = C[x_batch] # 토큰 임베딩 [B, S, E]
  1. 토큰 임베딩을 이어붙여 하나로 만든다.
embcat = emb.view(emb.shape[0], -1) # 벡터 합치기 [B, S*E]
  1. 첫번째 순방향 신경망(Linear)을 통과시킨다.
hprebn = embcat @ W1 + b1 # 활성화 함수 적용전 [B, H]
  1. batch normalization을 적용한다.
bnmeani = 1/n*hprebn.sum(0, keepdim=True) # 배치 차원에 따라 평균 계산[1, H]
bndiff = hprebn - bnmeani # broadcasted # 실제값 - 평균 [B, H]
bndiff2 = bndiff**2 # (실제값 - 평균)**2 [B, H]
bnvar = 1/(n-1)*(bndiff2).sum(0, keepdim=True) # 배치 차원에 따라 분산 계산 [1, H]
bnvar_inv = (bnvar + 1e-5)**-0.5 # [1, H]
bnraw = bndiff * bnvar_inv # 정규화 [B, H]
hpreact = bngain * bnraw + bnbias # BatchNorm의 가중치와 편향 더하기 [B, H]
  1. 활성화 함수(tanh)를 적용한다.
h = torch.tanh(hpreact) # tanh 활성화 함수 적용 [B, H]
  1. 두번째 순방향 신경망을 통과시켜 어휘 사이즈의 벡터로 변환한다.
logits = h @ W2 + b2 # logit 출력 [B, V]
  1. softmax를 적용하고 cross entropy 손실을 구한다.
logit_maxes = logits.max(1, keepdim=True).values #[B, 1]
norm_logits = logits - logit_maxes # 확률이 안정적으로 계산되도록 logits 값에서 두번째 차원의 최대값을 빼줌 [B, V]
counts = norm_logits.exp() # [B, V]
counts_sum = counts.sum(1, keepdims=True) #[B, 1]
counts_sum_inv = counts_sum**-1 # [B, 1]
probs = counts * counts_sum_inv # 확률값 계산 [B, V]
logprobs = probs.log() # 로그 함수 적용 [B, V]
loss = -logprobs[range(n), y_batch].mean() # 손실 계산 (scalar value)

전체 코드는 아래와 같다.

emb = C[x_batch] # 캐릭터를 벡터로 임베딩 [B, S, E]
embcat = emb.view(emb.shape[0], -1) # 변환된 캐릭터 벡터 합치기 [B, S*E]
# 레이어 1 연산
hprebn = embcat @ W1 + b1 # 활성화 함수 적용전 [B, H]
# BatchNorm 연산
bnmeani = 1/n*hprebn.sum(0, keepdim=True) # 배치 차원에 따라 평균 계산[1, H]
bndiff = hprebn - bnmeani # broadcasted # 실제값 - 평균 [B, H]
bndiff2 = bndiff**2 # (실제값 - 평균)**2 [B, H]
bnvar = 1/(n-1)*(bndiff2).sum(0, keepdim=True) # 배치 차원에 따라 분산 계산 [1, H]
bnvar_inv = (bnvar + 1e-5)**-0.5 # [1, H]
bnraw = bndiff * bnvar_inv # 정규화 [B, H]
hpreact = bngain * bnraw + bnbias # BatchNorm의 가중치와 편향 더하기 [B, H]
# 활성화 함수
h = torch.tanh(hpreact) # tanh 활성화 함수 적용 [B, H]
# 레이어 2
logits = h @ W2 + b2 # logit 출력 [B, V]
# 크로스 엔트로피 손실 계산 ( F.cross_entropy(logits, y_batch)와 같음 )
logit_maxes = logits.max(1, keepdim=True).values #[B, 1]
norm_logits = logits - logit_maxes # 확률이 안정적으로 계산되도록 logits 값에서 두번째 차원의 최대값을 빼줌 [B, V]
counts = norm_logits.exp() # [B, V]
counts_sum = counts.sum(1, keepdims=True) #[B, 1]
counts_sum_inv = counts_sum**-1 # [B, 1]
probs = counts * counts_sum_inv # 확률값 계산 [B, V]
logprobs = probs.log() # 로그 함수 적용 [B, V]
loss = -logprobs[range(n), y_batch].mean() # 손실 계산 scalar value

마지막으로 PyTorch의 backward를 이용해서 미분값을 자동으로 계산하자. retain_grad 메소드를 이용해서 계산된 값이 계산 그래프에서 맨 마지막 노드(leaf node)가 아니더라도 그래디언트를 확인할 수 있도록 설정할 수 있다. 

for p in parameters:
  p.grad = None
for t in [logprobs, probs, counts, counts_sum, counts_sum_inv, # afaik there is no cleaner way
          norm_logits, logit_maxes, logits, h, hpreact, bnraw,
         bnvar_inv, bnvar, bndiff2, bndiff, hprebn, bnmeani,
         embcat, emb]:
  t.retain_grad()
loss.backward()
loss

6. 그래디언트 검증

직접 계산한 그래디언트와 PyTorch의 미분 엔진을 통해 계산된 그래디언트를 비교하기 위해 다음과 같은 함수를 사용한다.

ex는 직접 계산한 그래디언트가 미분 엔진을 통해 계산된 그래디언트와 완전히 일치하는지를 의미하고, app은 완전히 일치하지는 않지만 두 값이 매우 유사하다는 것을 의미한다. maxdiff는 직접 계산한 그래디언트와 자동으로 계산된 그래디언트의 차이에 절대값을 적용했을 때 가장 큰 값을 나타낸다. 즉, 가장 큰 차이가 얼마정도인지 확인하기 위함이다.

def cmp(s, dt, t):
  ex = torch.all(dt == t.grad).item()
  app = torch.allclose(dt, t.grad)
  maxdiff = (dt - t.grad).abs().max().item()
  print(f'{s:15s} | exact: {str(ex):5s} | approximate: {str(app):5s} | maxdiff: {maxdiff}')

7. 역전파

이제 본격적으로 역전파 과정을 구현해보자. 역전파는 순전파와 반대 순서로 진행된다. 따라서 loss 값을 logprobs로 미분한 값을 먼저 구해야한다. loss는 next token에 대한 확률값에 대한 cross entropy의 평균한 값이다.

주의해야 할 점은 next token에 대한 확률값에 대해서만 cross entropy가 계산됐다는 점이다. next token을 제외한 나머지 토큰에 대한 확률값은 loss에 영향을 미치지 않는다. 따라서 그래디언트에 영향을 미치면 안된다. 이를 위해 one_hot 벡터를 사용한다. one_hot 벡터를 통해 시퀸스에서 next token의 인덱스에만 1의 값을 설정한다.

평균 연산은 전체값을 모두 더한 후 샘플의 수 (배치 사이즈)만큼 나누는 연산(1/n)을 곱해 값을 더한 것과 동일하다. 그래서 loss를 logprobs에 대해서 미분한 값은 다음과 같다.

# loss = -logprobs[range(n), y_batch].mean() # 손실 계산 scalar value
# dloss / dlogprobs
dlogprobs = -(1/n)* F.one_hot(y_batch, num_classes=vocab_size)

logprobs는 probs에 로그 함수를 적용한 것이다. 로그 함수의 미분은 다음과 같다.

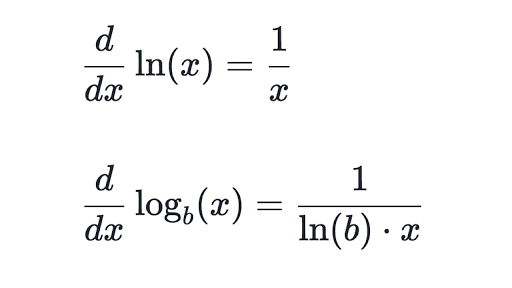
따라서 logprobs를 probs에 대해 미분한 값은 다음과 같이 계산된다. 연쇄 법칙(chain rule)에 의해 이전에 계산한 dlogprobs 값이 곱해졌다는 점을 주의하자. 

# logprobs = probs.log()
# dlogprobs / dprobs
dprobs = dlogprobs * probs**(-1)

probs는 counts와 counts_sum_inv의 곱이다. 따라서 probs를 counts_sum_inv에 대해 미분한 값은 counts이다.

주의해야할 것은 counts_sum_inv는 [B, 1] 사이즈의 텐서이지만, probs와 counts는 [B, V] 사이즈의 텐서라는 점이다. 즉, counts_sum_inv가 브로드캐스팅(broadcasting)되어 counts에 곱해져 probs가 되었단 의미이다. 브로드캐스팅으로 인해 하나의 변수가 계산에 여러번 사용되었다. 따라서 영향을 미친 모든 값에 대한 그래디언트를 더해줘야 한다. 따라서 그래디언트는 다음과 같이 계산된다. 

# probs = counts * counts_sum_inv 
# dprobs / dcounts_sum_inv
dcounts_sum_inv = (dprobs * counts).sum(1, keepdims=True)

counts_sum_inv는 단순히 counts_sum의 역수이다.따라서 counts_sum_inv를 counts에 대해 미분한 값은 멱 규칙에 의해 다음과 같이 계산된다.

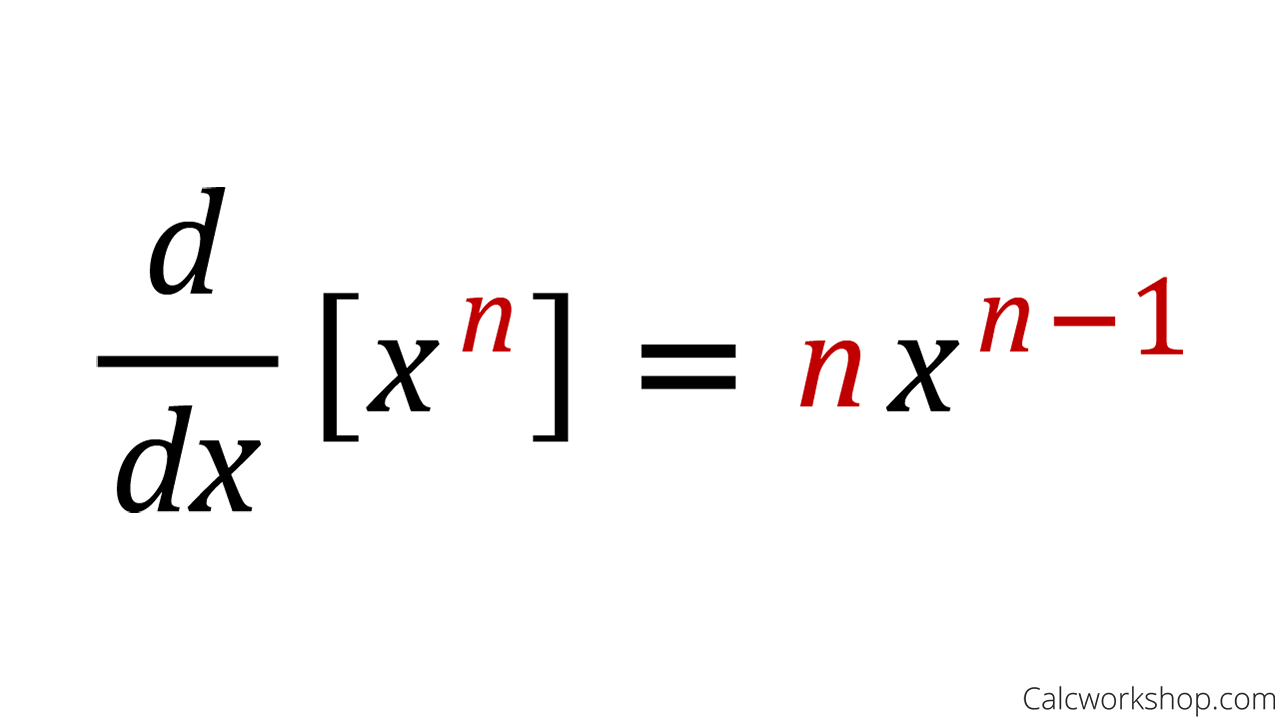
# counts_sum_inv = counts_sum**-1 
# dcounts_sum_inv / dcounts_sum 
dcounts_sum = dcounts_sum_inv * -(counts_sum)**(-2)

probs는 counts와 counts_sum_inv의 곱이기 때문에 probs를 counts에 대해 미분한 값은 다음과 같다.

# probs = counts * counts_sum_inv
# dprobs / dcounts
dcounts = dprobs * counts_sum_inv

counts_sum은 counts의 두번째 차원에 있는 값을 모두 더한 것이다. 더하기 연산의 미분은 이전 단계의 미분값을 흘려주는 것과 같다. 따라서 counts_sum을 counts에 대해 미분한 값은 다음과 같다. 주의할 점은 그래디언트가 이전에 계산한 dcounts에 더해진다는 것이다. 왜냐하면 counts가 계산 그래프에서 한 번 이상 사용되었기 때문에 counts가 loss에 미치는 영향을 구하기 위해서는 그래디언트를 더해줘야 한다.

# counts_sum = counts.sum(1, keepdims=True)
# dcounts_sum / dcounts
dcounts += dcounts_sum

counts는 norm_logits에 지수함수를 적용한 것이다. 지수함수의 미분은 다음과 같다. 미분값이 자신과 같다. 따라서 counts를 norm_logits에 대해 미분한 값은 다음과 같다.

ddxex=ex{d \over dx}e^{x}=e^{x}
# counts = norm_logits.exp() 
# dcounts / dnorm_logits
dnorm_logits = dcounts * norm_logits.exp()

norm_logits는 logits에 logit_maxes를 뺀 값이다. logit_maxes는 [B, 1] 사이즈의 텐서이기 때문에 [B, V] 사이즈인 logits와의 연산을 위해 브로드캐스팅이 적용된다. 따라서 norm_logits를 logit_maxes에 대해 미분한 값은 다음과 같다.

# norm_logits = logits - logit_maxes 
# dnorm_logits / dlogit_maxes
dlogit_maxes = (-dnorm_logits).sum(1, keepdims=True)

norm_logits를 logits에 대해 미분한 값은 이전 단계에 계산된 미분값과 같다. logit_maxes는 logits의 두번째 차원에서 최고값들이다. 따라서 logit_maxes를 logits에 대해 미분한 값은 이전 단계에 계산된 미분값 중에서 두번째 차원에서 최고값의 미분값이다. logits 역시 계산 그래프에서 한 번 이상 사용되었기 때문에 그래디언트를 누적해서 더해준다.

# norm_logits = logits - logit_maxes 
# logit_maxes = logits.max(1, keepdim=True).values #[B, 1]
# dnorm_logits / dlogits
dlogits = dnorm_logits.clone()
# dlogit_maxes / dlogits
dlogits += dlogit_maxes * F.one_hot(logits.max(1).indices, num_classes=logits.shape[1])

나머지 계산은 jupyter notebook을 통해 확인할 수 있다. 역전파에 대한 감을 잡기 위해 처음부터 스스로 계산해본다면 좋은 경험이 될 것이다.

profile
김회정
안녕하세요
이전 포스트

Transformer에 대한 이해

다음 포스트

언어 모델 (Language Model)

0개의 댓글