Heap

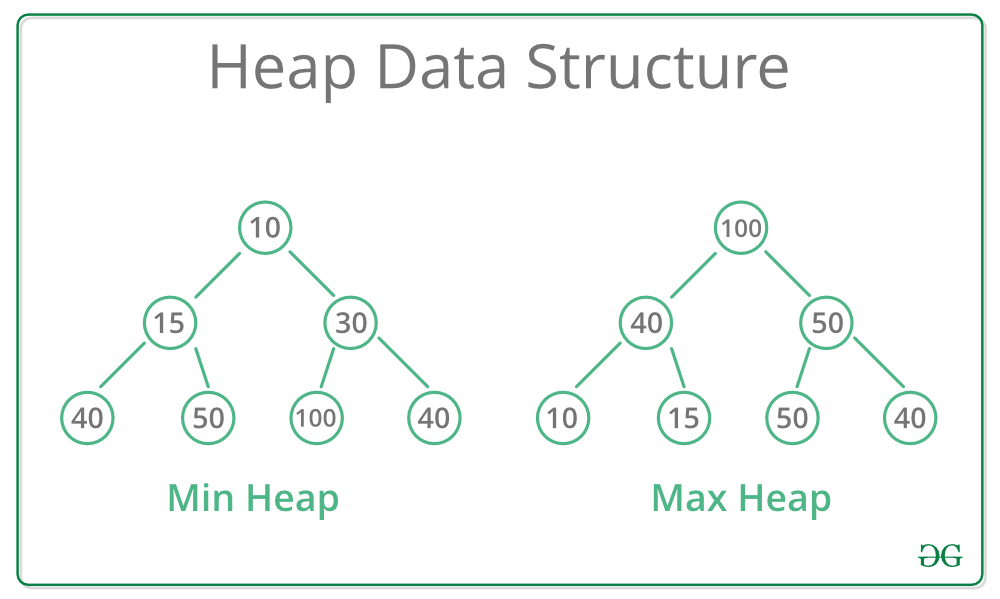
Heap은 자료구조 중 하나로, 완전 이진 트리(Complete Binary Tree)의 일종이다.
최소 힙(Min Heap)과 최대 힙(Max Heap) 두 가지 종류가 있으며
일반적으로 우선순위 큐(Priority Queue)나 힙 정렬(Heap Sort) 등의 알고리즘에서 사용된다.

heap-order

heap-order는 최소 힙(Min Heap) 또는 최대 힙(Max Heap)이 유지되는 성질이다.

Complete Binary Tree

높이 h를 가지는 heap의 특성은 다음과 같다.

◾ 높이가 i인 레벨에 있는 노드의 수는 $2^i$이다.

◾ 높이가 h인 레벨에서, 나머지 노드들은 해당 레벨에서 가장 왼쪽 가능한 위치에 위치한다.

◾ 힙의 마지막 노드는 해당 힙에서 가장 높은 depth에서 가장 오른쪽에 위치한 노드이다.

Height of a Heap

완전 이진 트리에서 노드의 개수가 n개인 heap의 높이는 $O(log\;n)$이다.
높이가 h일 때, 트리에 존재하는 노드의 개수는 $N =2^{(h + 1)} + 1$ 이므로
$h = O(log\;n)$이 된다.

Insertion into a Heap

Heap에 새로운 노드를 추가하는 방법은 다음과 같다.

◾새로운 노드를 Heap의 가장 마지막 노드의 오른쪽에 추가한다. 이때, Heap은 완전 이진 트리(Complete Binary Tree) 구조를 유지해야 한다.

◾ 새로운 노드를 부모 노드와 비교한다. 최소 힙에서는 새로운 노드의 값이 부모 노드의 값보다 작으면 Swap한다. 최대 힙에서는 새로운 노드의 값이 부모 노드의 값보다 크면 Swap한다.

◾부모 노드와 새로운 노드를 Swap한 후, 새로운 노드를 부모 노드로 설정하여 다시 2번 과정을 반복한다. 새로운 노드의 값이 더 이상 부모 노드의 값보다 작지 않거나 크지 않을 때까지 이 과정을 반복한다.

◾ 최종적으로 Heap의 Heap-Order(최소 힙 또는 최대 힙의 특성)가 유지되도록 새로운 노드를 삽입한다.

Upheap

Heap에서 새로운 노드를 삽입하면서 Heap-Order을 유지하기 위해 수행되는 과정을 Upheap이라고 한다. 다음은 그 과정을 나타낸다.

◾ 새로운 노드를 Heap의 가장 마지막 노드의 오른쪽에 추가한다.

◾ 새로운 노드를 부모 노드와 비교한다.

◾ 부모 노드와 새로운 노드를 Swap한 후, 새로운 노드를 부모 노드로 설정하여 다시 2번 과정을 반복한다.

◾ 최종적으로 Heap-Order가 유지되도록 새로운 노드를 삽입한다.

Removal from a Heap

Heap에 루트 노드를 제거하는 방법은 다음과 같다.

◾ Root 노드를 삭제한다.

◾가장 마지막 노드를 Root 노드의 자리에 놓는다.

◾새로운 Root 노드를 자식 노드와 비교한다.

◾비교한 자식 노드와 새로운 Root 노드를 Swap한다.

◾Swap한 자식 노드와 새로운 Root 노드를 다시 비교한다. Heap-Order가 유지될 때까지 이 과정을 반복한다.

◾최종적으로 Heap-Order가 유지되도록 삭제된 노드를 제거한다.

삽입과 삭제의 시간복잡도는 $O(log\;n)$이다.

Downheap

Heap에서 노드를 삭제하면서 Heap-Order을 유지하기 위해 수행되는 과정을 Downheap이라고 한다. 다음은 그 과정을 나타낸다.

◾ Root 노드 또는 삭제된 노드의 자리에 새로운 노드를 삽입한다.

◾ 새로운 노드를 자식 노드와 비교한다.

◾ 비교한 자식 노드와 새로운 노드를 Swap한다.

◾ Swap한 자식 노드와 새로운 노드를 다시 비교하며, Heap-Order가 유지될 때까지 이 과정을 반복한다.

Updating the Last Node

Heap에서 마지막 노드의 값을 변경하는 과정을 Updating the Last Node라고 한다. 이 과정은 힙에서 특정 노드의 값을 갱신할 때, 그 노드가 마지막 노드에 위치하고 있을 때 수행된다.

다음은 그 과정이다.

◾ 마지막 노드의 값을 변경한다.

◾ 변경된 마지막 노드를 부모 노드와 비교한다.

◾ 비교한 값을 부모 노드와 Swap한다.

◾ Swap한 부모 노드와 변경된 마지막 노드를 다시 비교하며, Heap-Order가 유지될 때까지 이 과정을 반복한다.

◾ 최종적으로 Heap-Order가 유지되도록 변경된 마지막 노드를 Upheap 또는 Downheap한다.

이 글은 다음과 이어진다.
다음 글