Recursion

함수를 재귀적으로 호출하는 것

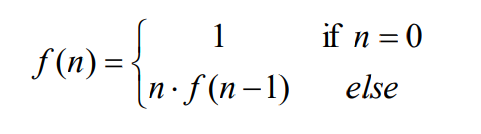
factorial

팩토리얼은 대표적인 재귀함수이다.

def factorial(n):
    
    if n <= 1:
        return 1
    else:
        return n * factorial(n-1)

Base case(s)

재귀 호출을 수행하지 않는 입력 변수의 값은 기본(base) 케이스라고하며(적어도 하나 이상의 기본 케이스가 있어야 함), 이러한 기본 케이스가 없으면 함수가 무한히 재귀 호출될 수 있다.

모든 재귀함수는 반드시 base case에 도달해야한다.

재귀호출

모든 재귀 함수는 base case로 향하도록 정의되어야 한다.

def LinearFibo(k):
    if k <= 1: # Base Case
        return (k, 0)
    else:
        (i, j) = LinearFibo(k - 1)
        return (i + j, i)

재귀함수를 이용해서 자 그리기

def draw_line(tick_length, tick_label = ''):
    line = '-' * tick_length
    if tick_label:
        line += ' ' + tick_label
    print(line)
    
def draw_interval(center_length):
    if center_length > 0:
        draw_interval(center_length - 1)
        draw_line(center_length)
        draw_interval(center_length - 1)

def draw_ruler(num_inches, major_length):
    draw_line(major_length, '0')
    for j in range(1, 1+num_inches):
        draw_interval(major_length - 1)
        draw_line(major_length, str(j))
        
if __name__ == '__main__':
    
    draw_ruler(2, 5)

이분탐색 구현하기

def binary_search(data, target, low, high):
    
    if low > high:
        return False
    
    else:
        mid = (low + high) // 2
        if target == data[mid]:
            return True
        elif target > data[mid]:
            return binary_search(data, mid + 1, high)
        else:
            return binary_search(data, low, mid - 1)

이분탐색 분석

이분탐색은 O(log n) 런타임을 가진다.

선형 재귀

선형 재귀는 재귀 호출이 한 번만 수행되는 기본적인 재귀 형태이다. 이 재귀 형태에서는 한 번의 재귀 호출을 수행하고, 이 재귀 호출이 기본 케이스로 수렴한다.

def LinearSum(a, n):
    if n == 1:
        return a[0]
    else:
        return LinearSum(a, n - 1) + a[n-1] #한 번의 재귀 호출

reverse함수 구현

def reverse(s, start, stop):
    if start < stop - 1:
        s[start], s[stop] = s[stop], s[start]
        reverse(s, start + 1 , stop  - 1)

Recursive Squaring Method 구현

def Power(x, n):
    if n == 0:
        return 1
    
    if n % 2 != 0:
        y = Power(x, (n-1) // 2)
        return x * y * y
    else:
        y = Power(x, n // 2)
        return y*y

Tail Recursion

Tail Recursion은 마지막에만 재귀호출을 발생시킨다.

Binary Recursion

Binary Recursion은 두 번의 재귀 호출이 존재한다.

def BinarySum(a, i, n):
    if n == 1:
        return a[i]
    
    return BinarySum(a, i, n//2) + BinarySum(a, i + n//2, n//2)

Fibonacci 함수

def fibo(n):
    if n <= 1:
        return n
    else:
        return fibo(n-1) + fibo(n - 2)

Linear Fibo

def LinearFibo(k):
    if k <= 1:
        return (k, 0)
    else:
        (i, j) = LinearFibo(k - 1)
        return (i + j, i)

Multiple Recursion

Multiple Recursion은 여러 번의 재귀 호출이 존재한다.

def PuzzleSolve(k, S, U):
    if k == 0:
        return "Solution found: " + str(S)
    else:
        for e in U:
            U.remove(e)
            S.append(e)
            if k == 1:
                if S_solve_puzzle(S):
                    return "Solution found: " + str(S)
                else:
                    PuzzleSolve(k - 1, S, U)
            U.append(e)
            S.pop()

def S_solve_puzzle(S):
    # implement puzzle solving logic here
    pass