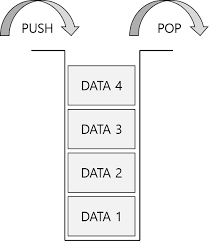
Stack

스택은 삽입과 삭제가 last-in first-out 방식으로 이루어 집니다.

Operation

주요 오퍼레이션은 다음과 같다.

push(object): 요소를 삽입하는 함수

pop(): 마지막으로 삽입된 요소를 삭제하고 반환하는 함수

top(): 마지막으로 삽입된 요소를 삭제 없이 반환하는 함수

len(): 저장된 요소의 갯수를 반환하는 함수

is_empty(): 스택이 비었는지의 유무를 검사하는 함수

Array-based Stack

Array based stack은 배열을 이용하여 구현된 스택 자료구조이다.
이 구조는 일반적으로 콜스택(Call Stack), 역추적(Backtracking), 깊이 우선 탐색(DFS, Depth First Search) 등 다양한 알고리즘에서 활용된다.

특징

◾ 삽입과 삭제가 빠르다. (각각의 연산이 $O(1)$의 러닝타임을 가진다.)
◾ 크기를 동적으로 조절하는 것이 어렵다.
◾ 배열의 크기를 초과할 경우 스택이 오버플로우(Overflow) 상태가 될 수 있다.
◾ n개의 요소에 대해 $O(n)$의 공간을 차지한다.

구현

class ArrayStack:
    
    def __init__(self):
        self.data = []
    
    def __len__(self):
        return len(self.data)
    
    def is_empty(self):
        return len(self.data) == 0
    
    def push(self, e):
        self.data.append(e)
    
    def top(self):
        if self.is_empty():
            raise ValueError("Stack is Empty")
        return self.data[-1]
    
    def pop(self):
        if self.is_empty():
            raise ValueError("Stack is Empty")
        return self.data.pop()

Parentheses Matching Algorithm

from ArrayStack import ArrayStack

def is_mathcing(expr):
    lefty = '({['
    righty = ')}]'
    S = ArrayStack()
    for c in expr:
        if c in lefty:
            S.push(c)
        elif c in righty:
            if S.is_empty():
                return False
            if righty.index(c) != lefty.index(S.pop()):
                return False
    return S.is_empty()

def is_matched_Html(raw):
    S = ArrayStack()
    j = raw.find('<')
    while j != -1:
        k = raw.find('>', j+1)
        if k == -1:
            return False
        tag = raw[j+1, k]
        if not tag.startswith('/'):
            S.push(tag)
        else:
            if S.is_empty():
                return False
            if tag[1:] != S.pop():
                return False
        j = raw.find('<', k+1)
    return S.is_empty()

Algorithm for Evaluating Expressions

# Python3 program to evaluate a given
# expression where tokens are
# separated by space.

# Function to find precedence
# of operators.
def precedence(op):
	
	if op == '+' or op == '-':
		return 1
	if op == '*' or op == '/':
		return 2
	return 0

# Function to perform arithmetic
# operations.
def applyOp(a, b, op):
	
	if op == '+': return a + b
	if op == '-': return a - b
	if op == '*': return a * b
	if op == '/': return a // b

# Function that returns value of
# expression after evaluation.
def evaluate(tokens):
	
	# stack to store integer values.
	values = []
	
	# stack to store operators.
	ops = []
	i = 0
	
	while i < len(tokens):
		
		# Current token is a whitespace,
		# skip it.
		if tokens[i] == ' ':
			i += 1
			continue
		
		# Current token is an opening
		# brace, push it to 'ops'
		elif tokens[i] == '(':
			ops.append(tokens[i])
		
		# Current token is a number, push
		# it to stack for numbers.
		elif tokens[i].isdigit():
			val = 0
			
			# There may be more than one
			# digits in the number.
			while (i < len(tokens) and
				tokens[i].isdigit()):
			
				val = (val * 10) + int(tokens[i])
				i += 1
			
			values.append(val)
			
			# right now the i points to
			# the character next to the digit,
			# since the for loop also increases
			# the i, we would skip one
			# token position; we need to
			# decrease the value of i by 1 to
			# correct the offset.
			i-=1
		
		# Closing brace encountered,
		# solve entire brace.
		elif tokens[i] == ')':
		
			while len(ops) != 0 and ops[-1] != '(':
			
				val2 = values.pop()
				val1 = values.pop()
				op = ops.pop()
				
				values.append(applyOp(val1, val2, op))
			
			# pop opening brace.
			ops.pop()
		
		# Current token is an operator.
		else:
		
			# While top of 'ops' has same or
			# greater precedence to current
			# token, which is an operator.
			# Apply operator on top of 'ops'
			# to top two elements in values stack.
			while (len(ops) != 0 and
				precedence(ops[-1]) >=
				precedence(tokens[i])):
						
				val2 = values.pop()
				val1 = values.pop()
				op = ops.pop()
				
				values.append(applyOp(val1, val2, op))
			
			# Push current token to 'ops'.
			ops.append(tokens[i])
		
		i += 1
	
	# Entire expression has been parsed
	# at this point, apply remaining ops
	# to remaining values.
	while len(ops) != 0:
		
		val2 = values.pop()
		val1 = values.pop()
		op = ops.pop()
				
		values.append(applyOp(val1, val2, op))
	
	# Top of 'values' contains result,
	# return it.
	return values[-1]

# Driver Code
if __name__ == "__main__":
	
	print(evaluate("10 + 2 * 6"))
	print(evaluate("100 * 2 + 12"))
	print(evaluate("100 * ( 2 + 12 )"))
	print(evaluate("100 * ( 2 + 12 ) / 14"))

# This code is contributed
# by Rituraj Jain