Tree

트리(Tree)는 계층적 구조를 표현하기 위해 사용되는 비선형(nonlinear) 데이터 구조이다. 트리는 하나의 루트(root) 노드에서 시작하여 여러 개의 자식(child) 노드들로 이루어진 계층 구조를 갖는다.

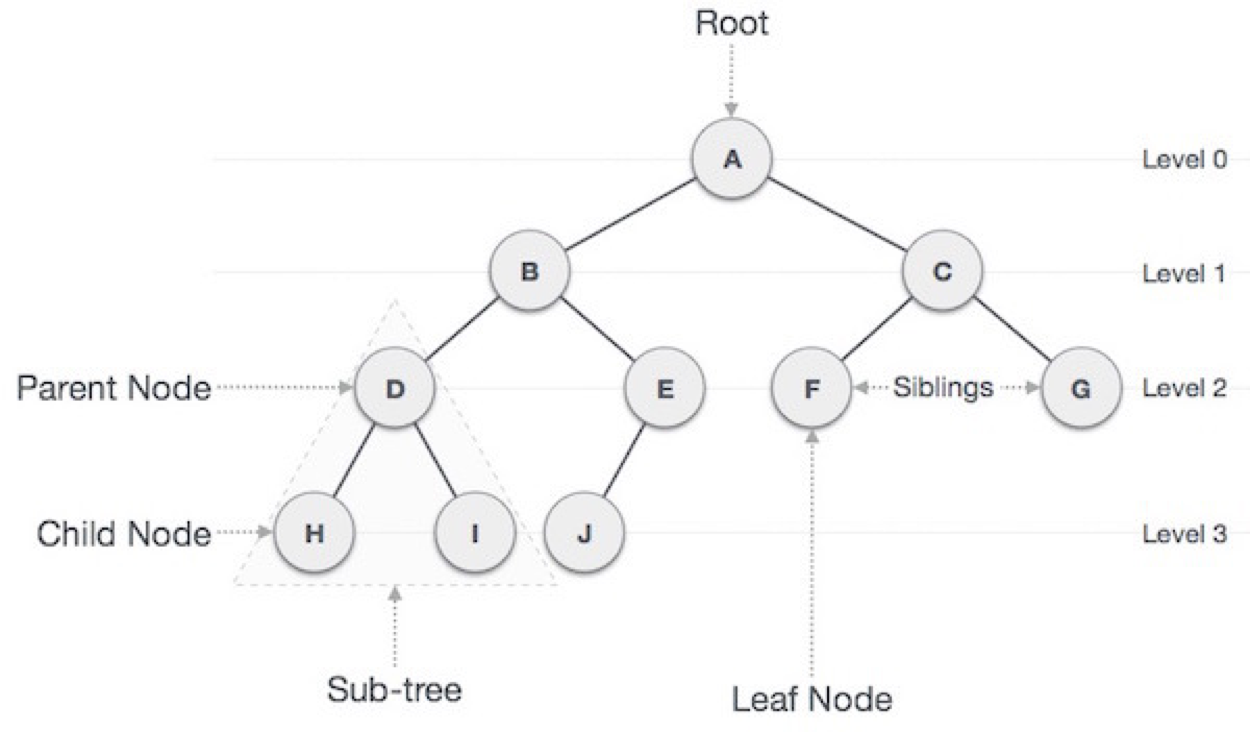
Root

부모 노드가 없는 노드이다. 위 사진에선 A 노드가 root 노드이다.

Internal node

최소 한 개의 자식을 가지는 노드이다. A, B, C, D, E가 해당된다.

External node

자식 노드가 없는 노드이다. J, F, G가 해당된다.

Ancestors

부모 노드와 같이 자신 노드의 상위 노드를 일컫는다. H 노드의 조상 노드 A, B, D이다.

Depth

조상 노드의 수이다. H 노드의 경우 3이다.

Height

노드의 최대 depth이다. 위 사진의 height은 3이다.

Descendant

자식 노드와 같이 자신 노드의 하위 노드를 일컫는다. D 노드의 자손 노드는 H, I이다.

구현

class Tree:
    class Position:
        
        def element(self):
            raise NotImplementedError("must be implemented by subclass")
        
        def __eq__(self, other):
            raise NotImplementedError("must be implemented by subclass")
        
        def __ne__(self, other):
            return not (self == other)
        
    def root(self):
        raise NotImplementedError("must be implemented by subclass")
    
    def parent(self, p):
        raise NotImplementedError("must be implemented by subclass")
    
    def num_children(self, p):
        raise NotImplementedError("must be implemented by subclass")
    
    def children(self, p):
        raise NotImplementedError("must be implemented by subclass")
    
    def __len__(self):
        raise NotImplementedError("must be implemented by subclass")
    
    def is_root(self, p):
        return self.root() == p
    
    def is_leaf(self, p):
        return self.num_children(p) == 0
    
    def is_empty(self):
        return len(self) == 0

추상 클래스 Tree를 작성한 것이다.

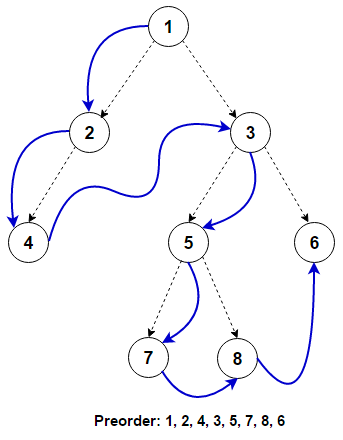
Preorder Traversal(전위순회)

Preorder Traversal은 이진 트리(Binary Tree)의 탐색 방법 중 하나이다. 탐색 순서는 다음과 같다.

◾ 노드를 방문한다.
◾ 왼쪽 서브트리를 방문한다.
◾ 오른쪽 서브트리를 방문한다.

예시)

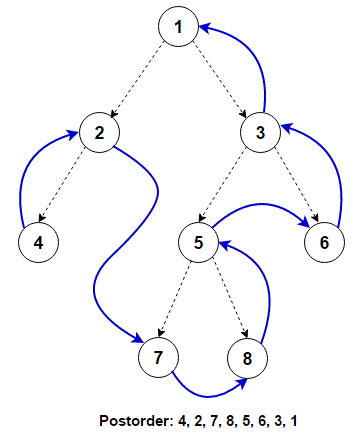
Postorder Traversal(후위순회)

Postorder Traversal은 이진 트리(Binary Tree)의 탐색 방법 중 하나이다. 탐색 순서는 다음과 같다.

◾ 왼쪽 서브트리를 방문한다.
◾ 오른쪽 서브트리를 방문한다.
◾ 노드를 방문한다.

예시)

Breadth-First Tree Traversal

Breadth-First Tree Traversal은 이진 트리(Binary Tree)의 탐색 방법 중 하나로, 루트 노드(root node)를 시작으로 레벨(level) 단위로 탐색하는 방법이다. 즉, 한 레벨의 모든 노드를 방문한 후, 그 다음 레벨의 모든 노드를 방문하는 방법이다.

예시)

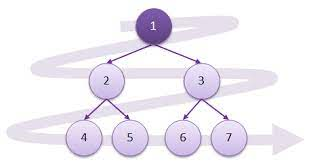
Binary Tree

이진 트리(Binary Tree)는 각 노드가 최대 두 개의 자식 노드를 갖는 계층적(hierarchical) 데이터 구조이다. 이진 트리는 루트 노드(root node)를 가지며, 각 노드는 왼쪽 서브 트리(left subtree)와 오른쪽 서브 트리(right subtree)로 구성된다.

이진 트리에서 각 노드는 자신의 부모 노드와 자식 노드를 가리키는 포인터(pointer)를 갖는다.
부모 노드는 최대 하나의 자식 노드를 가질 수 있으며, 자식 노드가 없는 경우도 가능하다.

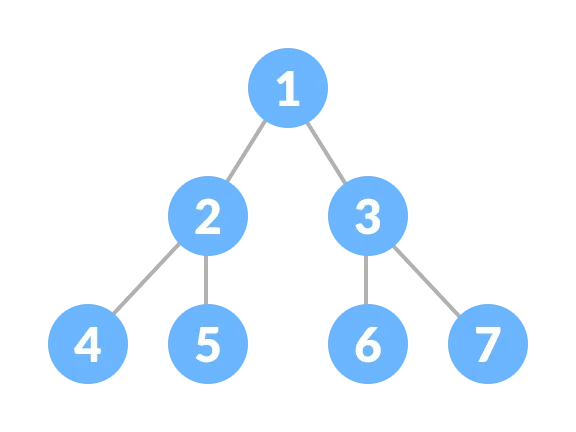
Properties of Proper Binary Tree

Proper Binary Tree란 각 노드가 최대 두 개의 자식 노드를 갖는 이진 트리(Binary Tree)로, 다음과 같은 특징을 가진다.

◾ 각 내부 노드는 정확히 두 개의 자식 노드를 갖는다.

◾ 루트 노드(root node)를 포함한 모든 노드는 왼쪽 자식 노드와 오른쪽 자식 노드를 순서대로 갖는다.

Proper Binary Tree는 이진 탐색 트리(Binary Search Tree) 등에서 많이 사용되며, 이진 탐색 트리에서는 왼쪽 서브 트리의 모든 노드가 현재 노드의 값보다 작고, 오른쪽 서브 트리의 모든 노드가 현재 노드의 값보다 크다는 조건을 만족한다.

Proper Binary Tree의 노드 수와 깊이는 다음과 같은 관계를 가진다.

◾ Proper Binary Tree의 노드 수는 $2^{(h+1)} - 1$개이다.

◾ $h ≥ log_2(n + 1) - 1$

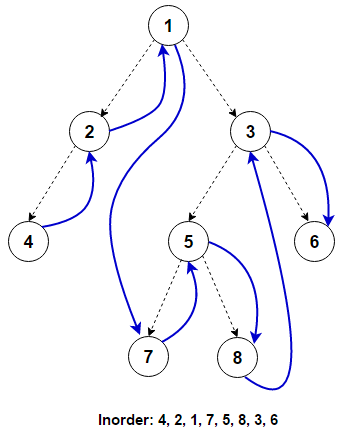
Inorder Traversal(중위순회)

Inorder Traversal(중위순회)는 다음과 같이 노드를 방문한다.

◾ 왼쪽 서브트리를 방문한다.
◾ 노드를 방문한다.
◾ 오른쪽 서브트리를 방문한다.

예시)

Arithmetic Expression Tree

def print_expression(v):
    if v.left is not None:
        print("(", end="")
        print_expression(v.left)
    
    print(v.element(), end="")
    
    if v.right is not None:
        print_expression(v.right)
        print(")", end="")

Evaluate Arithmetic Expressions

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None
        
def build_expression_tree(postfix_expression):
    stack = []
    for token in postfix_expression:
        if token.isdigit():
            node = Node(int(token))
            stack.append(node)
        else:
            right_node = stack.pop()
            left_node = stack.pop()
            node = Node(token)
            node.left = left_node
            node.right = right_node
            stack.append(node)
    return stack.pop()

def evaluate_expression_tree(node):
    if node.left is None and node.right is None:
        return node.data
    
    left_value = evaluate_expression_tree(node.left)
    right_value = evaluate_expression_tree(node.right)
    if node.data == '+':
        return left_value + right_value
    elif node.data == '-':
        return left_value - right_value
    elif node.data == '*':
        return left_value * right_value
    elif node.data == '/':
        return left_value / right_value
    
def euler_tour(node, traversal):
    if node is not None:
        traversal.append(node.data) # 첫 번째 방문
        if node.left is not None:
            euler_tour(node.left, traversal)
            traversal.append(node.data) # 두 번째 방문
        if node.right is not None:
            euler_tour(node.right, traversal)
            traversal.append(node.data) # 세 번째 방문
    
if __name__ == '__main__':
    postfix_expression = ['5', '2', '+', '3', '*', '4', '-', '2', '/']
    s = []
    root_node = build_expression_tree(postfix_expression)
    result = evaluate_expression_tree(root_node)
    result2 = euler_tour(root_node, s)
    #print(result) # 출력값: 8.5
    print(s)

Euler Tour Traversal

Euler Tour Traversal은 다음과 같은 순서로 노드를 방문한다.

◾ 현재 노드를 전위순회(preorder) 방법으로 방문한다.

◾ 현재 노드의 왼쪽 서브 트리를 Euler Tour Traversal 방법으로 방문한다.

◾ 현재 노드를 중위순회(inorder) 방법으로 방문한다.

◾ 현재 노드의 오른쪽 서브 트리를 Euler Tour Traversal 방법으로 방문한다.

◾ 현재 노드를 후위순회(postorder) 방법으로 방문한다.

예시)