썸네일 출처

---

컴퓨팅 사고력

---

수와 표현

---

1) 정수

유클리드 호제

큰 것에서 작은 것을 빼서 0이 나올때까지 반복하면 (MOD로 빼기 대체)

에라토스테네스의 체 (Sieve of Eratosthenes)

2, 3, 5, 7 ... 의 배수를 지워가면서 소수를 구하기

트릭) 하나의 수를 소수 판별할 때 2부터~제곱근 까지만 판별해도 가능하다!

스턴-브로코트 트리 (Stern-Brocot tree)

중간분수(Mediant) 활용

a/b 와 c/d의 중간분수는 (a+c)/(b+d) 로 정의
이를 반복적으로 적용하여 모든 기약분수를 찾을 수 있다.

GiYak class 만들어서 활용

확장 유클리드 호제 (sw 5640번)

1단계: 유클리드 호제법 적용
최대 공약수를 구하는 과정을 기록

2단계: 역추적을 통한 해 구하기

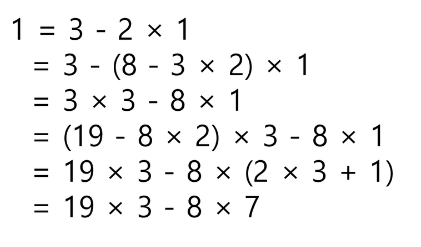
페르마 소정리 (sw 5607번)

언제써먹을 수 있을까?

p = 1000000007 (분할정복 필수!)

---

2) 관계식 유도

RSA

nQueen

절대값 (sw 2805)

당구 (sw 24309)

Collatz (sw 24268) -> 그리디 (sw 24303)

Greedy 나무 (sw 14510)

---

디오판토스 (sw 5640)

유클리드 호제를 확장하여 풀이

---

정답 코드

import java.util.Scanner;

public class Solution_5640_디오판토스 {

    static int T;
    
    public static void main(String[] args) {
        Scanner scann = new Scanner(System.in);
        
        // 테스트 케이스 수 입력
        T = scann.nextInt();
        
        for (int t = 1; t <= T; t++) {
            int a = scann.nextInt();
            int b = scann.nextInt();
            int c = scann.nextInt();
            
            // ax + by = c
            int d = gcd(a, b);
            
            // c가 gcd(a,b)의 배수인지 확인 (정수해가 존재하기 위한 조건)
            if (c % d == 0) {
                // a, b를 d로 나누고 c도 d로 나눈다
                int a1 = a / d;
                int b1 = b / d;
                int c1 = c / d;
                
                // 확장 유클리드 알고리즘으로 a1*x + b1*y = 1의 해를 구함
                long[] r = exgcd(a1, b1);
                // r[0]는 gcd, r[1]은 x, r[2]는 y
                
                // 구한 해에 c1을 곱해서 원래 방정식의 해를 구함
                long x = r[1] * c1;
                long y = r[2] * c1;
                
                System.out.println("#" + t + " " + x + " " + y);
            } else {
                // 정수해가 없는 경우 (실제로는 문제에서 답이 항상 있다고 보장함)
                System.out.println("#" + t + " No integer solution exists.");
            }
        }
        scann.close();
    }
    
    // 확장 유클리드 알고리즘: ax + by = gcd(a,b)의 해 (x,y)를 구함
    // 반환 배열: [gcd(a,b), x, y]
    public static long[] exgcd(long a, long b) {
        if (b == 0) return new long[] {a, 1, 0};
        else {
            long[] coef = exgcd(b, a % b);
            long tmp = coef[1] - coef[2] * (a / b);
            coef[1] = coef[2];
            coef[2] = tmp;
            return coef;
        }
    }
    
    // 최대공약수 구하기
    public static int gcd(int m, int n) {
        if (m == 0) {
            return n;
        } else if (n == 0) {
            return m;
        } else if (m > n) {
            return gcd(m % n, n);
        } else {
            return gcd(m, n % m);
        }
    }
}

---

풀이

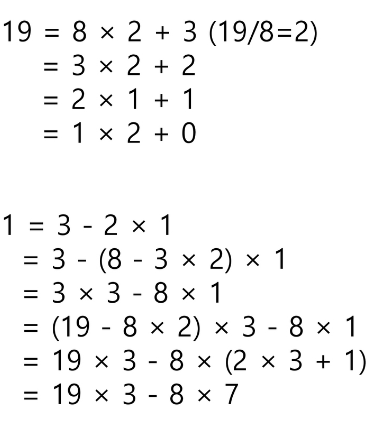
코드의 흐름 계속 나누어서 들어간 후 식을 만들어내면서 백트래킹으로 올라온다.
long[0] 은 최대공약수를 저장해 두었는데 이 값이 1로 되게 하기 위해 최대공약수로 전부 나눠준 값으로 함수에 넣는다.
마지막으로 c의 값을 곱해주어 해 x,y를 찾을 수 있다!

---

숙제

벨로그 정리 마무리, 정처기 실기 공부