많이 생각을 하고 들어왔는 지 모르겠지만, 정답은 스택 하나를 데이터를 넣을 때 사용하고, 나머지 스택을 데이터를 뺄 때 사용한다.
기본적으로 Stack은 후입선출, Queue는 선입선출이다. 그렇기에 먼저 들어오는 것이 나가도록 하기 위해서는 두번째 스택으로 전부 이동시키고 빼면 된다.
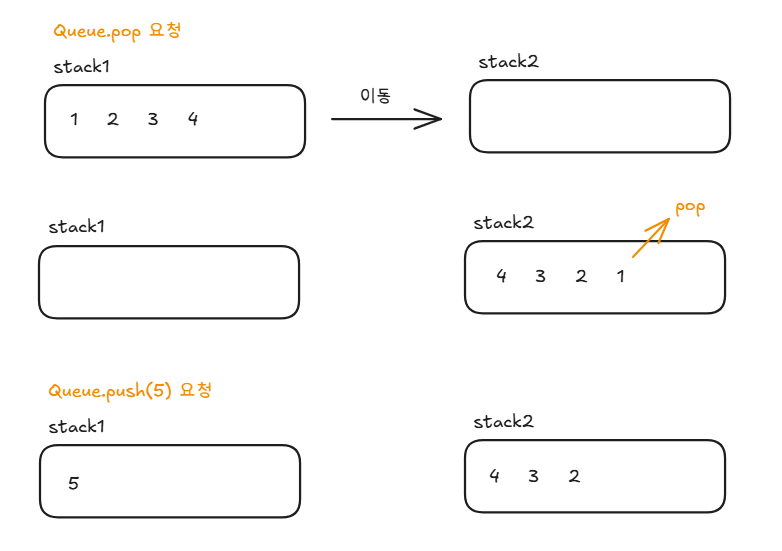
여기서 중요한 점은 stack2가 비었을 때만 stack1에서 stack2로 이동을 하고, 그 이후에는 stack1에 쌓아두면 된다. (나는 처음에 push 요청에서 stack2에서 stack1으로 이동했다)
그럼 정답 코드를 확인해보자.
import java.util.ArrayList;
import java.util.Stack;
public class TwoStackQueue {
Stack<Integer> stack1;
Stack<Integer> stack2;
public TwoStackQueue(){
stack1 = new Stack<>();
stack2 = new Stack<>();
}
public void push(int x){
// push는 단순하게 stack1에 push 한다.
stack1.push(x);
}
public int pop(){
// stack2 가 비었을 때 stack1에 있는 값을 모두 넣는다.
if(stack2.isEmpty()){
while(!stack1.isEmpty()){
stack2.push(stack1.pop());
}
}
// 넣었는데도 비어있다면 pop 할 수 없다.
if(stack2.isEmpty()){
System.out.println("스택이 비어있습니다!");
return -1;
}
// 역순으로 들어간 stack2 에서 pop을 하니 첫번째 값이 나간다.
return stack2.pop();
}
}
이렇게 잘 나오는 것을 확인할 수 있다.
여기서 중요한 것은 이제 이 코드가 O(1)로 작동한다는 점이다. 정확히 말하면 Amortized O(1)이다.
Amortized(분할 상환) 시간 복잡도를 조금 풀어서 얘기하자면, 최악의 경우가 가끔 발생해도, 평균적으로는 효율적이라는 뜻이다.
push 는 stack1에 push만 하는 것이니 정말 O(1)이고, pop이 만약에 stack2가 비어있을 때 O(N)의 순회를 통해서 값을 전달해야 하는데 이때만 오버헤드가 존재하고 평균적으로는 n개의 요소를 처리하면 총 2n번의 작업이므로 각 연산은 O(1) 이라고 할 수 있는 것이다.
이런 경우를 다른 곳에서도 볼 수 있는데 대표적인 예시로 ArrayList 동적 배열이 존재한다.
만약에 ArrayList에 계속해서 값을 추가한다고 하면, 평소에는 O(1)만큼이 들것이다. 하지만 배열이 꽉 차게 된다면 크기를 2배로 늘리고 복사하는 작업이 들어가게된다. 이 때는 O(N)만큼 시간이 동작하게 되겠지만 평균적으로는 O(1) 즉 Amortized O(1)의 시간복잡도를 가지게 되는 것이다.

