Graphics Pipeline

• 3차원 컴퓨터 그래픽스에서 그래픽스 파이프라인(graphics pipeline) 또는 렌더링 파이프라인(rendering pipeline)은 3차원 이미지를 2차원 래스터 이미지로 표현을 하기위한 단계적인 방법을 말합니다.

  • 여기서 래스터(raster)란 컴퓨터에서 화상 정보를 표현하는 한 가지 방법으로 이미지를 2차원 배열 형태의 픽셀로 구성하고 이 점들의 모습을 조합, 일정한 간격의 픽셀들로 하나의 화상 정보를 표현하는 것을 말합니다.
  • 즉, 한 줄에서 연속된 픽셀들의 집합을 래스터라고 합니다.

• 다음은 Direct3D 12 의 Graphics Pipeline 입니다.

• Graphics Pipeline 은 크게 두 종류의 단계들로 구성되어 있습니다.

Fixed Pipeline

• GPU 에서 모든 처리가 진행되며 응용 프로그램에서 변경할 수 없는 단계

  • 정해진 연산만 수행하므로 수행하므로 프로그래머가 GPU 연산에 관여할 수 없습니다. 즉, non-programmable 한 단계입니다.

• Graphics Pipeline 에서 Fixed Pipeline 에 해당하는 단계는 다음과 같습니다.

  • Input Assembler (IA)
  • Tesselator (TS)
  • Stream Output (SO)
  • Rasterizer (RS)
  • Output Merger (OM)

Programmable Pipeline

• 응용 프로그램에서 쉐이더 프로그램을 통해 제공해야 하는 단계

  • 프로그래머가 GPU 연산에 직접 관여할 수 있습니다. 즉, programmable 한 단계입니다.
  • Shaders 라고도 불립니다.

• Graphics Pipeline 에서 Shader stages 에 해당하는 단계는 다음과 같습니다.

  • Vertex Shader (VS)
  • Hull Shader (HS)
  • Domain Shader (DS)
  • Geometry Shader (GS)
  • Pixel Shader (PS)

• 이제, 각 단계들을 세부적으로 살펴봅시다.

Input Assembler (IA) Stage

• 응용 프로그램에서 제공받은 Vertex 버퍼의 Vertex 데이터(점, 선, 삼각형)를 다른 파이프라인 단계에서 사용할 Primitive 데이터(Line List, Triangle List 등)로 조립하여 다른 그래픽 파이프라인에서 사용할 수 있도록 준비하는 단계입니다.

  • 즉, 메모리에서 기하 자료(Vertex 데이터, Index)를 읽어 기하학적 기본 도형(삼각형, 선분 등)을 조립합니다.

• 또한,Index 버퍼를 이용하여 Vertex 의 복제나 중복을 막습니다.

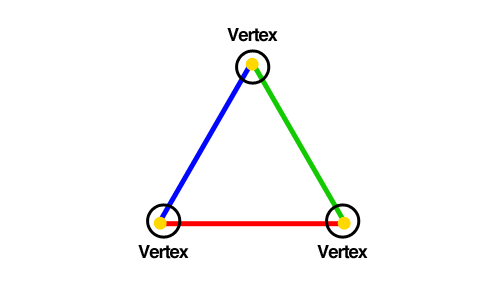
Vertex

• 수학적으로, 한 삼각형의 정점은 두 변이 만나는 점입니다. 선분의 경우 선분의 양 끝점이 정점이고, 하나의 점의 경우에는 그 점 자체가 정점입니다.

• Direct3D 에서의 정점은 공간적 위치, 즉 위치 값 이외의 정보를 담고 있으며 이를 통해 좀 더 복잡한 렌더링 효과를 구현할 수 있습니다.

  • 예를 들면 조명 구현을 위해 정점에 법선 벡터를 추가하거나 텍스처를 적용하기 위해 텍스처 좌표를 추가하는 식으로 사용할 렌더링 효과에 따라 특정 정보를 추가할 수 있는 유연성을 갖고 있습니다.

Primitive

• 기본적인 정의는 더 작은 상태로 쪼개거나 분해할 수 없는 '무언가' 또는 기하학적인 형태를 이르는 말입니다. 몇 가지 기본적인 타입이 존재하는데 Point List, Line List, Line Strip, Triangle List, Triangle Strip 등이 있습니다.

• 정점들은 정점 버퍼라고 하는 Direct3D 자료구조 안에 담겨서 렌더링 파이프라인에 묶입니다. 정점 버퍼는 정점들을 연속적인 메모리에 저장하는 자료구조일 뿐이기 때문에 정점 버퍼 자체는 그 정점들을 어떤 식으로 조합해서 기본 도형을 생성할 것인지 말해주지 않습니다. 이 생성 방식을 Direct3D 에게 알려주는 데에 쓰이는 수단이 Primitive 입니다.

  • 대부분은 삼각형 목록(Triangle List)을 기본 도형 위상 구조로 사용합니다. 이는 대부분의 Mesh 가 수많은 삼각형으로 근사하여 표현되기 때문입니다.

Point List

D3D12_PRIMITIVE_TOPOLOGY_POINTLIST

• 모든 정점은 개별적인 점으로 그려집니다.

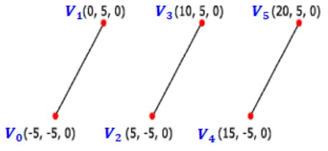
Line List

D3D12_PRIMITIVE_TOPOLOGY_LINELIST

• 매 정점 두 개가 개별적인 하나의 선분을 형성합니다. 2n 개의 정점으로 n 개의 선분이 만들어집니다.

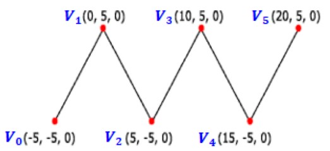
Line Strip

D3D12_PRIMITIVE_TOPOLOGY_LINESTRIP

• 정점들이 차례로 이어져 일련의 선분들이 그려집니다. Line List 와 다르게 정점을 따라 자동으로 선분이 이어집니다.

Triangle List

D3D12_PRIMITIVE_TOPOLOGY_TRIANGLELIST

• 매 정점 세 개가 하나의 개별적인 삼각형을 형성합니다. 3n 개의 정점으로 n 개의 삼각형이 만들어집니다.

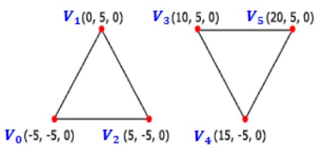
Triangle Strip

D3D12_PRIMITIVE_TOPOLOGY_TRIANGLESTRIP

• 정점들이 연결되어 일련의 삼각형들을 형성합니다. n 개의 정점으로 n - 2 개의 삼각형들이 만들어집니다.

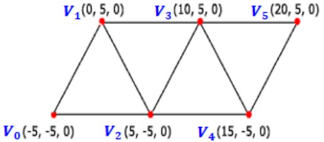
Index

• 앞서 언급했지만 3차원 물체의 기본 구축 요소는 삼각형입니다.

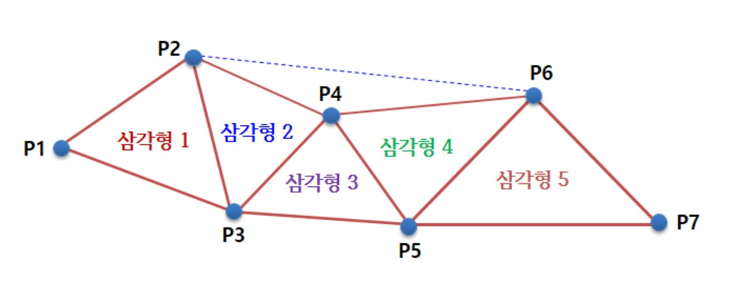
• 그림의 삼각형들은 다수의 정점들을 공유하고 있습니다.

  • 삼각형 1과 삼각형 2는 정점 P2 와 P3를 공유하고 있습니다. 즉 2개의 정점에서 2번 중복이 있습니다다.
  • 심지어 삼각형 2, 3, 4는 정점 P4 를 공유하고 있어 하나의 정점이 3번 중복됩니다. 이 중복 현상은 물체가 더 복잡해져 많은 삼각형으로 표현해야 하는 경우 더 심각해집니다.

• 정점들의 중복이 바람직하지 않은 이유는 크게 두 가지입니다.

  • 메모리 요구량 증가 -> 같은 정점을 여러 번 저장하기 때문
  • 그래픽 하드웨어 처리량 증가 -> 같은 정점 자료를 여러 번 처리하기 때문

• 따라서 Triangle List 에서 중복 정점들을 제거하는 방법은 가치가 있는 일입니다. 이 방법을 Index 가 제공합니다. 고유한 정점들로 정점 목록을 만들면, 어떤 정점을 어떤 순서로 사용해서 삼각형을 형성하는지를 그 정점들의 색인을 나열하여 지정하면 됩니다.

// 정점 버퍼
Vertex v[7] = {P1, P2, P3, P4, P5, P6, P7};

// 인덱스 버퍼
UINT indexList[] = {
    0, 1, 2, // 삼각형 1
    1, 3, 2, // 삼각형 2
    2, 3, 4, // 삼각형 3
    3, 5, 4, // 삼각형 4
    4, 5, 6  // 삼각형 5
};

• 그래픽 카드는 정점 목록의 고유한 정점들을 처리한 후, Index 목록을 이용하여 정점들을 조합해 삼각형을 형성합니다. Index 간의 중복이 생겼지만 두 가지 이유로 큰 문제가 되지 않습니다.

  • Index 는 정수이므로 정점 구조체보다 적은 양의 메모리를 차지합니다.
  • 정점 캐시 순서가 좋은 경우 그래픽 하드웨어는 중복된 정점들을 처리하지 않아도 됩니다.

Vertex Shader (VS) Stage

• Input Assembler 단계에서 출력되는 Primitive 의 각 Vertex 에 대한 연산을 수행합니다.

  • 정점 쉐이더는 항상 모든 정점들에 대해 한 번씩 실행되고, 하나의 정점에 대해 한 번만 호출됩니다. 이는 Pipeline 에서 항상 수행이 되어야 하는 단계이므로 정점에 대한 변환이 필요하지 않아도 정점 쉐이더를 생성해 연결해야 합니다.

• Vertex Shader 함수의 구체적인 내용은 프로그래머가 구현해서 GPU 에 전달하게 됩니다. 이 함수는 각 정점에 대해 GPU 에서 실행되기 때문에 속도가 빠릅니다.

• 변환(Transformation), 스키닝(Skinning), 조명(Vertex Lighting) 등 수많은 특수 효과를 정점 쉐이더에서 수행할 수 있습니다. 또한 입력 정점 자료는 텍스쳐, 변환 행렬, 장면 광원 정보 등 GPU 메모리에 담긴 다른 자료에도 접근할 수 있습니다.

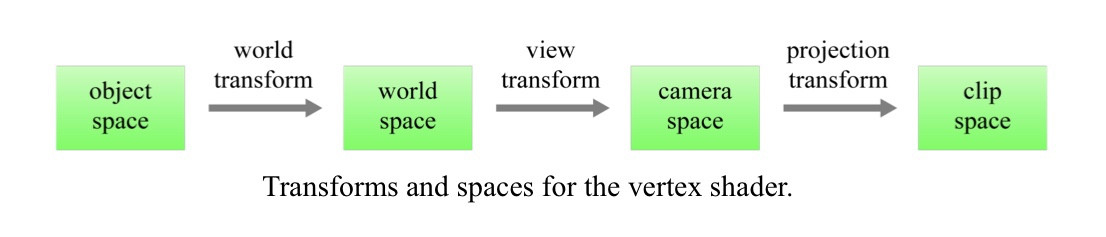
• 위와 같이 Vertex Shader 에서는 world transform, view transform, projection transform 등 의 좌표계 변환이 이루어지는데, 이에 대해 알아보겠습니다.

World Transform

• 물체가 가지는 object space 에서 정의된 물체를 world 에 두는 데 필요한 transform 입니다.

• object space 에서 작업을 하면 좌표계 원점을 물체의 중심 가까이에 둘 수 있고 좌표축들을 물체에 맞게 정렬할 수 있기 때문에 편합니다. 따라서 object space 에서 작업을 하여 3차원 모형 정점들을 모두 정의했다면 그것들을 world space 에 적절한 위치와 방향으로 배치해야 합니다.

  • 이를 위해 object space 와 world space 의 관계를 정의할 수 있어야 합니다. 즉, world space 기준으로 좌표 변경 변환을 수행해야 합니다.
  • 이를 World Transform 이라고 합니다.

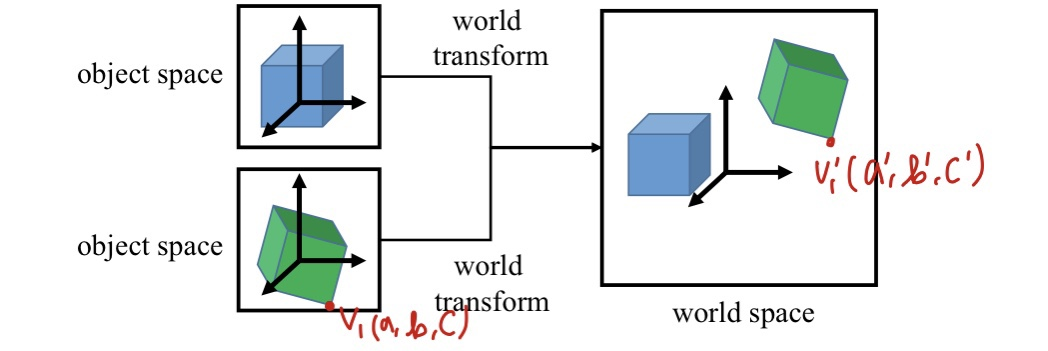
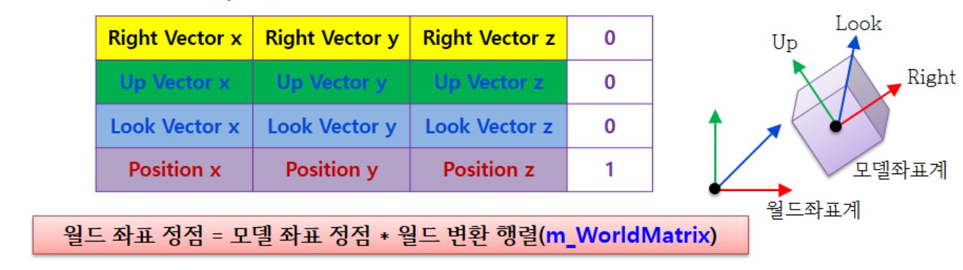
• World Transform 에 사용하는 변환 행렬을 세계 행렬(world matrix)이라고 부릅니다. 장면의 모든 물체에는 각자의 world matrix 가 있고, 각 물체를 world transform 하고 나면 모든 물체의 모든 좌표가 동일한 좌표계(세계 공간)를 기준으로 한 것이 됩니다.

• 변환 행렬은 어떻게 정의되는지 한번 살펴봅시다.

• 공간을 나타내는 벡터에 행렬을 곱한다는 것은 벡터를 변환하는 것입니다. 즉, 행렬이 곧 변환을 해주는 매개체라고 할 수 있습니다.

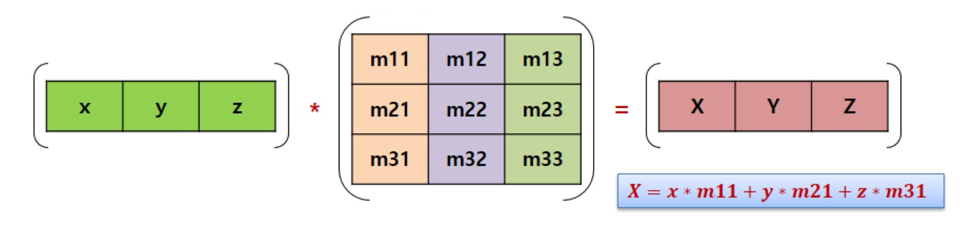
• 행렬에서 (1, 1) (2, 2) (3, 3) 위치의 값들은 크기를 나타냅니다. 각각의 값들을 조정하고 물체를 나타내는 정점 벡터들과 곱하면 물체가 x축, y축, z 축으로 크기가 늘거나 줄어듭니다. 이 행렬을 Scale(S) 이라고 합시다.

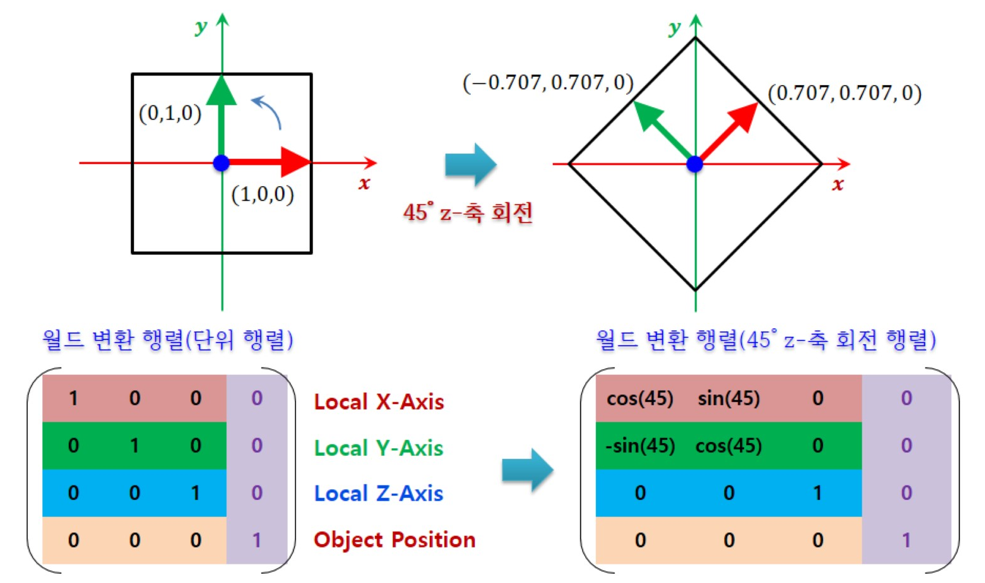
• 그리고 각 축마다 회전도 표현이 가능합니다.

• 여기서 세타 값을 정해준 뒤 물체 정점 벡터들과 곱하면 물체가 세타 값만큼 x, y, z 축으로 회전합니다.

  • x, y, z 축 모두 회전하고 싶다면 각각의 세타 값을 지정한 후 위 3개의 행렬을 차례대로 곱해주면 됩니다.

• x축 회전 행렬 y축 회전 행렬 z 축 회전 행렬의 값을 Rotate(R) 이라고 합시다.

• 이제 크기와 회전을 변환하였으니 이동을 변환할 차례입니다. 하지만 벡터는 이동에 대해 불변한 특성을 갖고 있기 때문에 3x3 행렬은 평행이동을 표현할 수 없습니다. 이동은 오직 점에만 적용되기 때문에 우리는 동차 좌표계를 사용하여 점과 벡터를 동일한 방식으로 다룰 수 있게 해야 합니다.

• 동차 좌표계는 x, y, z에서 w 를 추가한 것입니다. 4차원 벡터 (x, y, z, w)가 있다면 이는
  x1 = x/w, y1 = y/w, z1 = z/w 인 (x1, y1, z1)과 동차입니다.

  • 즉, 4차원 벡터의 x, y, z 를 w 로 나누는 작업은 4차원 벡터를 3차원 벡터로 투영(Projection)하는 것입니다. 이는 w가 1인 경우 3차원 벡터로 직접 대응됩니다. 4차원 벡터의 w값을 0으로 설정하는 경우에는 이동 변환이 적용되지 않습니다.

• 동차 좌표계를 사용하여 평행이동을 표현하기 위한 행렬은 다음과 같습니다.

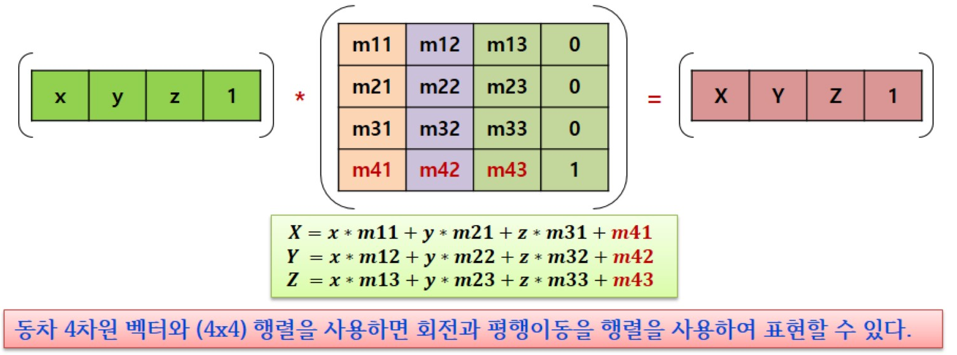
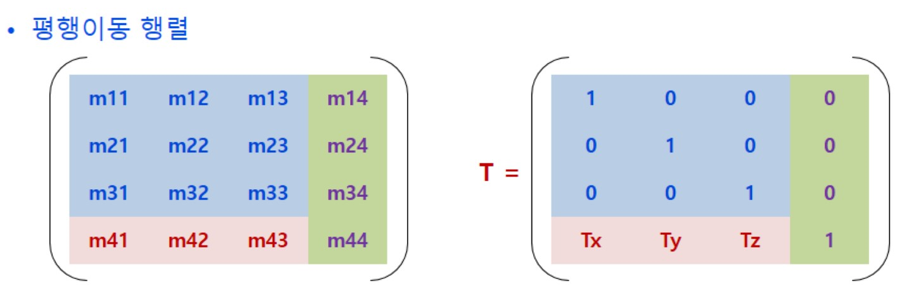
• 이와 같은 평행이동 행렬을 Transform(T)이라고 합시다.

• 이제 모든 변환들을 살펴봤으니 종합해주면 됩니다. 크기, 회전, 이동 순으로 변환 행렬을 곱한 값을 물체의 정점 벡터와 곱해주면 물체를 올바르게 world space 상에 놓을 수 있게 됩니다.

  • 즉, 월드 변환 행렬(world transform matrix)을 W 라고 했을 때 W = SRT 입니다.

View Transform

• 3차원 장면의 2차원 이미지를 만들어 내려면 장면에 가상의 카메라를 배치해야 합니다. 그 카메라는 world 에서 보이는 영역을 결정합니다. 그 영역이 바로 프로그램에서 2차원 이미지로 만들어 모니터에 표시할 영역입니다.

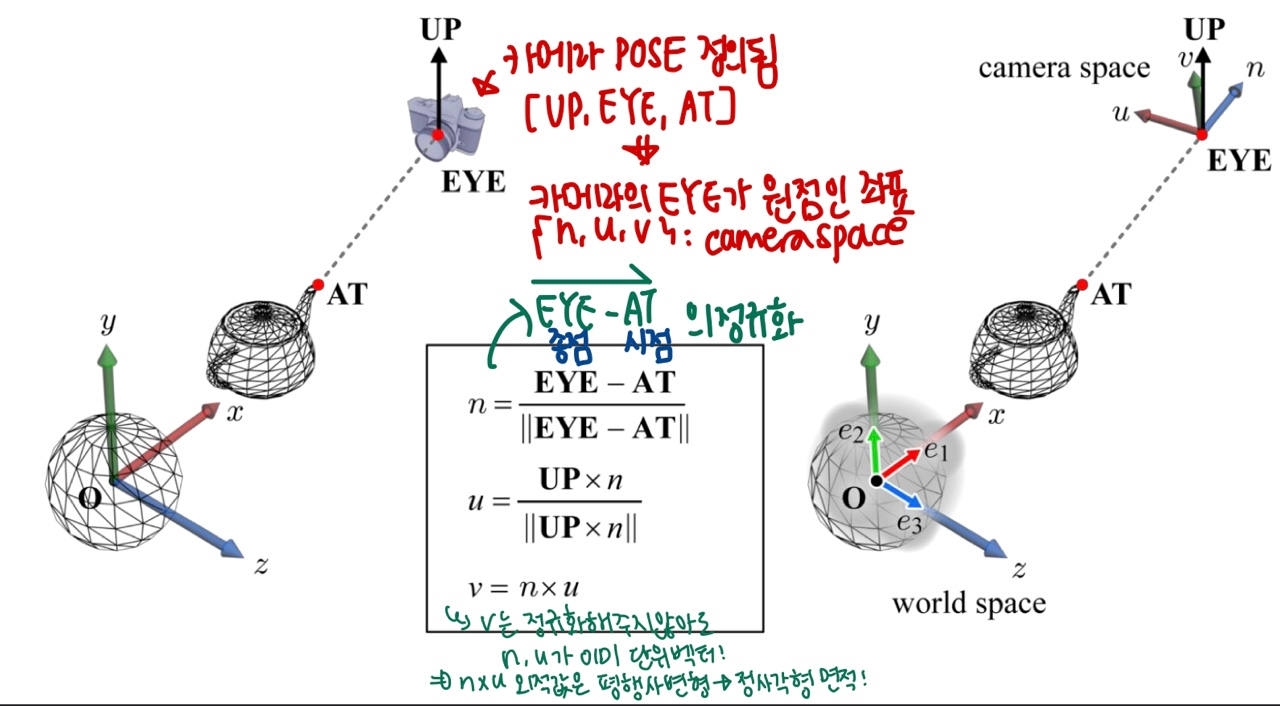
• 위 그림처럼 가상 카메라를 중심으로 Camera space 를 부여한다고 합시다. 이 좌표계는 카메라 공간 또는 시야 공간(view space)을 정의합니다.

• Camera 의 Pose 는 EYE, AT, UP 을 가집니다.

  • EYE : 카메라 위치
  • AT : 카메라가 향하는 방향
  • UP : 카메라가 가리키는 위치의 up 벡터 (카메라의 위아래로 꺾이는 정도)

• 이 카메라를 중심으로 {u, v, n} 벡터를 만들 수 있고, 이 세 기저는 직교 기저입니다.

  • n벡터 : EYE-AT 벡터의 정규화
  • u벡터 : UP벡터와 n의 외적의 정규화
  • v벡터 : n x u

• 이 벡터는 Camera Space의 축이 됩니다.

하지만 World Space 와 Camera Space 의 공간 축의 좌표가 다릅니다. Camera Space 의 세 축 벡터도 하나의 도형이라고 생각하고, 이를 World Space 에 겹치도록 변환해줄 수 있습니다.

• 이를 위해서는 Translation 과 Rotation 의 과정이 필요합니다.

Translation

• 평행 이동은 덧셈으로 나타낼 수 있습니다. 따라서 Homogeneous Coordinate 를 도입해서 행렬의 곱셈으로 바꿔줄 수 있기 때문에 4x4 matrix을 가지게 됩니다.

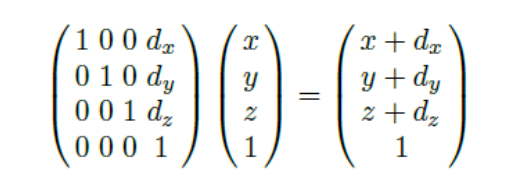
• 이를 활용하여 EYEx, EYEy, EYEz 의 좌표를 넣어서 Translation 시킨 좌표의 값을 얻을 수 있습니다.

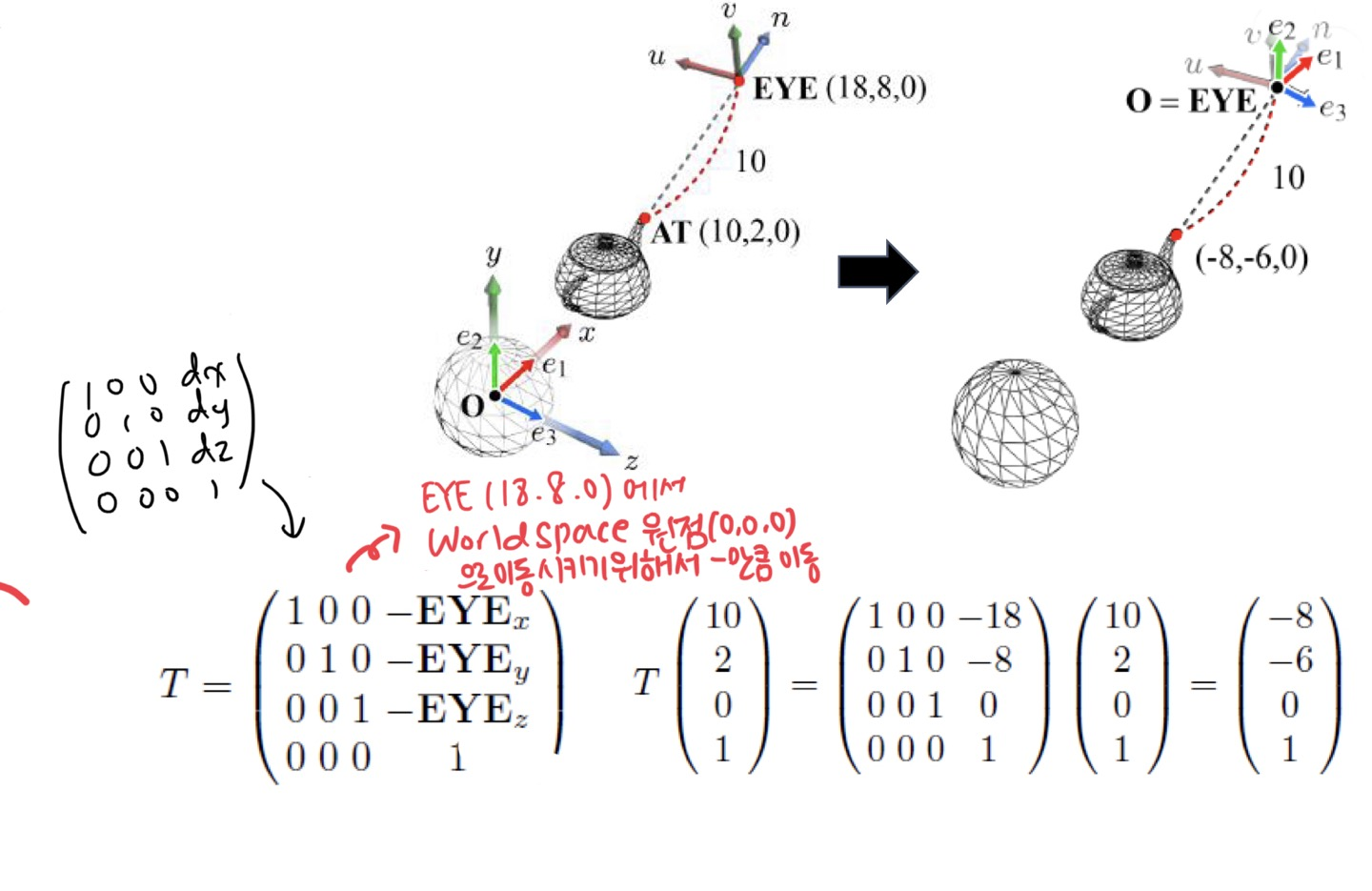
• (18,8,0) 의 위치를 가지는 camera space 의 EYE 위치로 world space 에서 원점을 이동시키기 위해, 물체 기준에서 EYE 만큼 평행 이동시켜줍니다. 이를 위해 음수 부호를 붙여서 Translation Matrix T 를 만들고, World Space 에서의 좌표와 곱하여 Camera Space 에서 쓰이는 좌표 값을 얻을 수 있습니다.

  • 이렇게 하면 EYE 좌표가 원점을 기준으로 translation 된 값을 얻을 수 있습니다.

하지만 위의 그림과 같이 평행이동만 해서는 축이 일치하지 않습니다.

• 따라서 Rotation 도 해야합니다.

Rotation

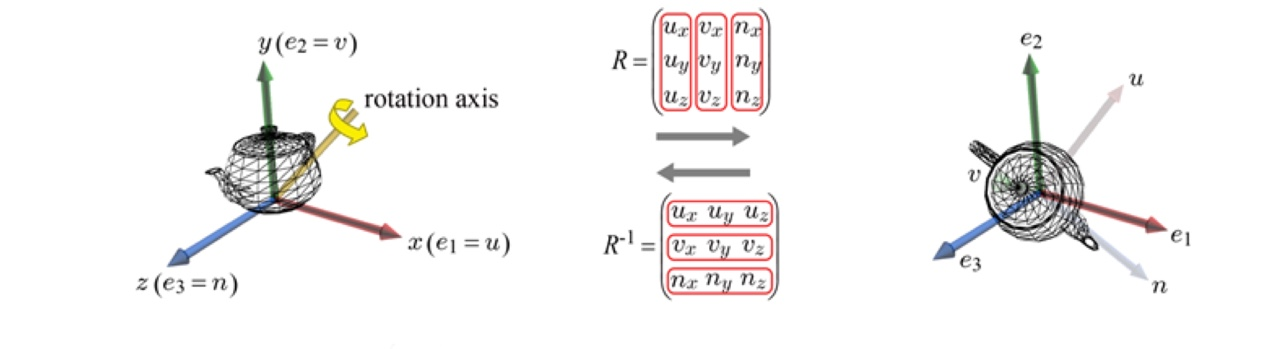
• 회전 변환을 기저의 관점에서 보면 얼마의 각도로 회전하는지 회전 행렬 R 을 구해서 좌표와 곱셈을 해주지 않아도 기저의 전치행렬로 회전 행렬 R 을 구할 수 있습니다.

Rotation and Object-space Basis

• 앞서 언급한 것처럼, 회전 변환을 Basis(기저)의 관점에서 볼 수 있습니다.

• {e1, e2, e3} : 월드 좌표계에 나타나는 standard basis 입니다.

  • 기저 벡터끼리 서로 수직이고, 크기는 1인 벡터입니다.

• {u, v, n} : 오브젝트 좌표계에서 나타나는 orthonormal basis 입니다.

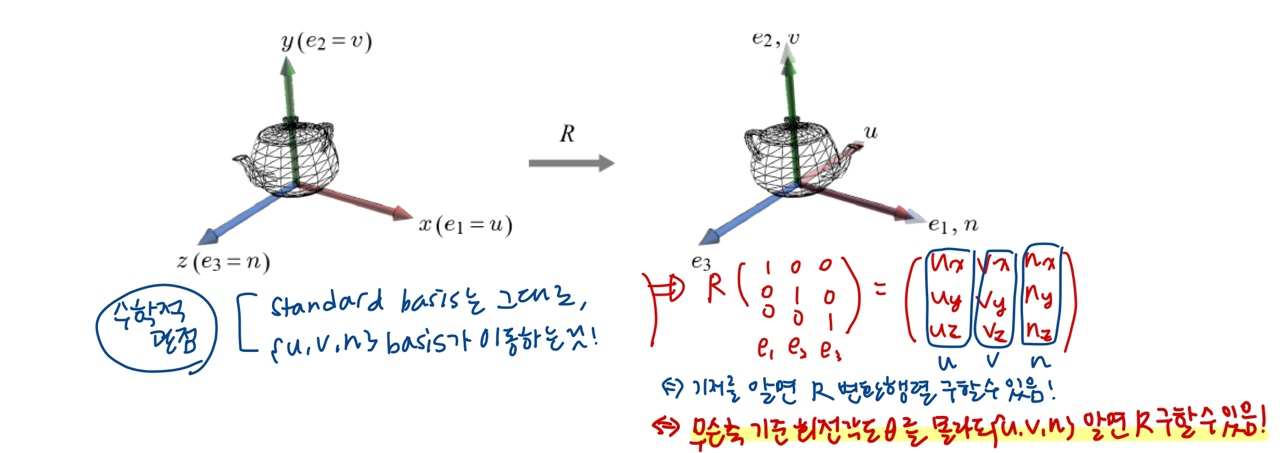
• 수학적인 관점에서 보면, 처음 {e1, e2, e3} == {u, v, n} 인 좌표계에서 한 오브젝트를 '회전'시킨다는 것은, 월드 좌표계인 {e1, e2, e3} 값은 변함이 없고, 오브젝트 좌표계가 가지는 {u, v, n} 기저들이 이동한 것이라고 생각할 수 있습니다.

• 회전 변환 행렬 R 에 {e1, e2, e3} (단위 행렬)을 곱한 값은 오브젝트가 회전을 나타낸 행렬인 {u v n} 행렬로 나타낼 수 있습니다.

  • 즉, 회전하는 값에 대한 기저를 알면 R 변환 행렬을 구할 수 있습니다. 따라서 θ값을 알지 못해도 R matrix 를 구할 수 있습니다.

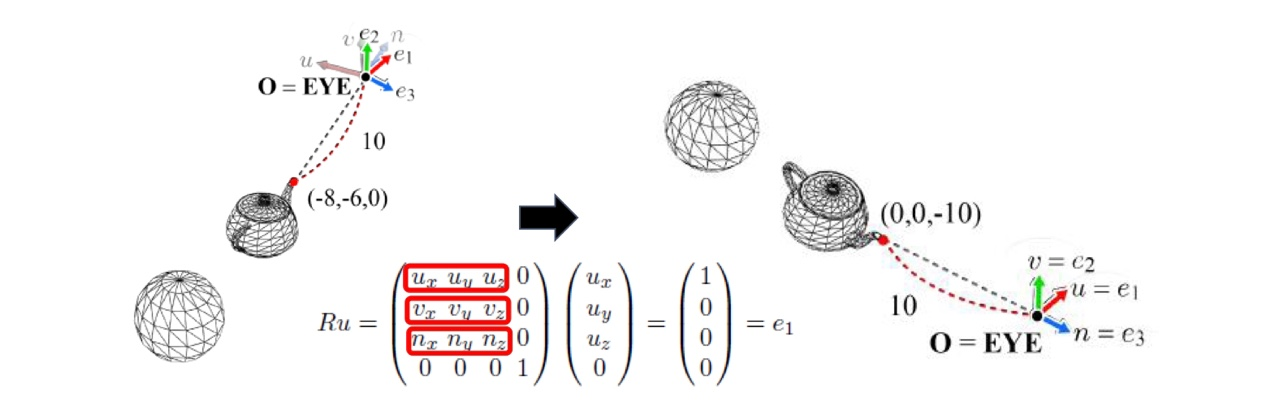
• 따라서 카메라 Space 의 회전 행렬 R 도 같은 방법으로 구할 수 있습니다.

View Transformation

• Translation 과 Rotation 과정을 합친 변환입니다.

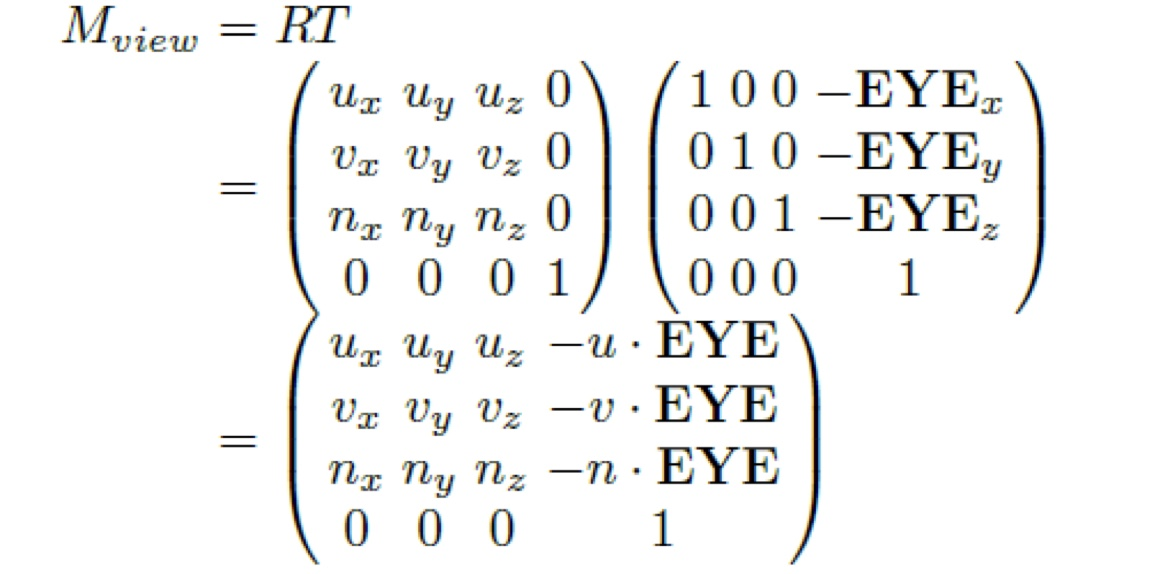
• 다음과 같이 View Transform Matrix 를 세울 수 있습니다.

  • World Transform 은 Object 별로 정의할 수 있습니다. 따라서 View Transform 은 World 별로 정의할 수 있는 것입니다.

Projection Transform

• Camera Space 상에 배치된 오브젝트들(3D)을 우리가 모니터로 보는 2D 화면 창 하나에 투영시켜서 볼 수 있도록 Projection Transform 을 수행해야 합니다.

View Frustum

• 카메라 상의 모든 물체를 화면에 담을 수 없기 때문에, 카메라의 시야각 범위 안에 있는 오브젝트만 투영시키도록 합니다.

• view frustum : 화면의 visible 한 영역만 나타내는 절두체를 view frustum 이라고 합니다.

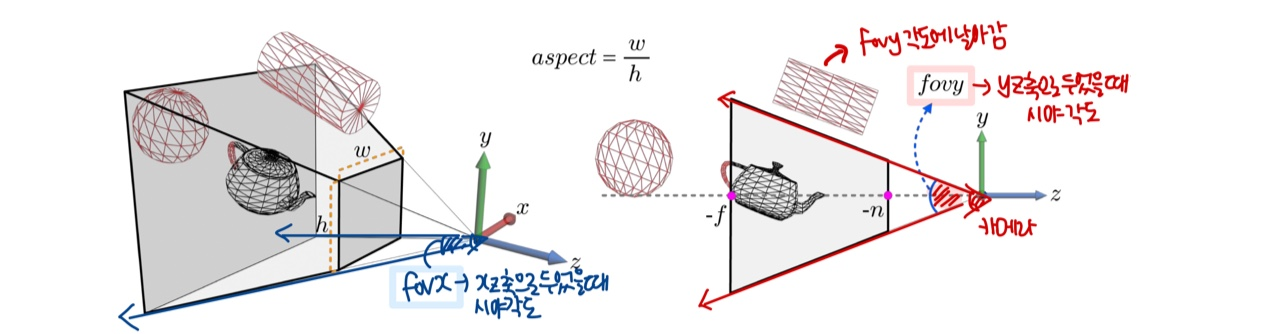
• fovy (field of view y-axis) : 시야각, y-z 축으로 두었을 때 카메라로부터 물체를 바라볼 때 생기는 각도
• n & f : near & far
• aspect : w(넓이) / h(높이) 로, view frustum의 종횡비

Culling and Clipping

• Vertex 연산을 줄이기 위해 연산이 필요없는 부분은 culling 시켜줍니다.

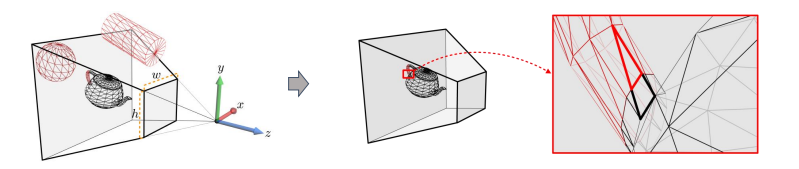
Culling

• GPU rendering pipeline 이전에 view frustum 바깥쪽에 있는 오브젝트를 버려서 렌더링 하지 않도록 합니다.

Clipping

• view frustum 내부에 오브젝트 전체가 들어있는 것이 아니라 경계에 걸친 경우입니다. 이 때, frustum 내부에 있는 오브젝트만 처리해줍니다.

  • 이 과정은 rasterization stage 에서 진행합니다.

Clip Space

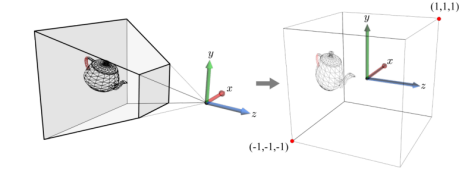
• Clipping 은 피라미드형이 아닌, 정육면체 공간에서 처리합니다.
• view frustum 을 2x2x2 정육면체로 옮겨 clip space 로 변환하는 과정을 Projection Transform 이라고 합니다.

Lighting

• 광선으로 밝게 비춤 또는 그 광선을 나타냅니다.

• 3D 공간에는 빛이 없지만 현실 세계의 빛을 3요소로 만들어 흉내냅니다.

  • 조명의 요소에는 정반사광(Specular), 난반사광(Diffuse), 환경광(Ambient) 등이 있습니다.

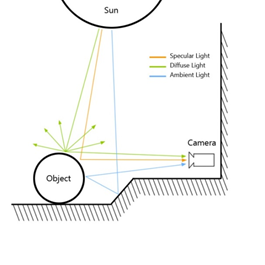
• 3가지 광원으로 방향성 광원(Directional Light), 점 광원(Point Light), 스포트 광원(Spot Light)이 있습니다.

다시, Projection Transform

View Frustum to Cube

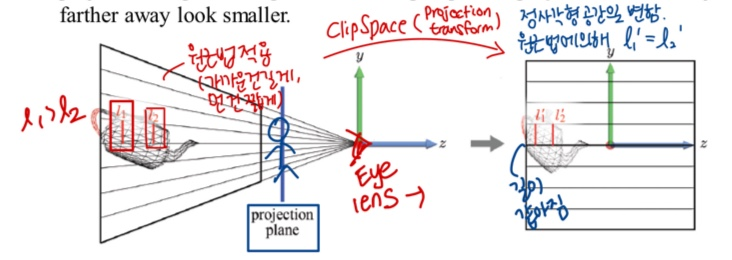
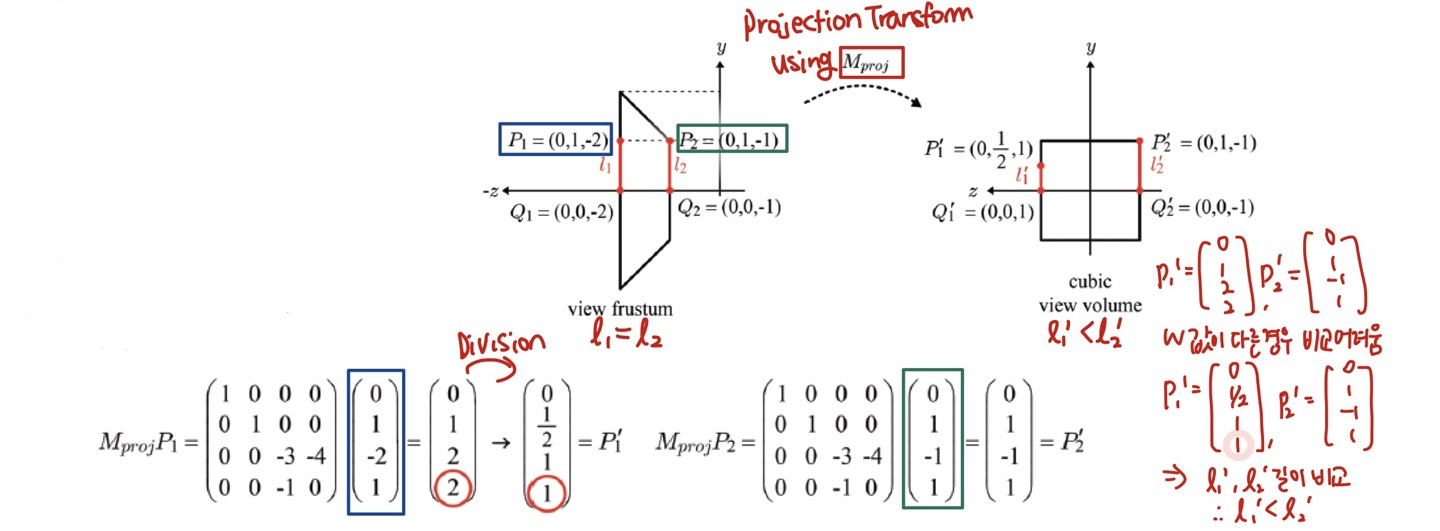
• camera(EYE) 위치에서 projection plane 에 대해 바라봤을 때, view frustum을 cube 로 옮겨줍니다. 원근법에 의해 L1 과 L2 의 길이는 cube 에서 같아집니다.

Derivation of projection transform matrix

• View frustum 을 cube 로 옮길 때 projection transform 에 필요한 행렬과 수식을 이해해봅시다.

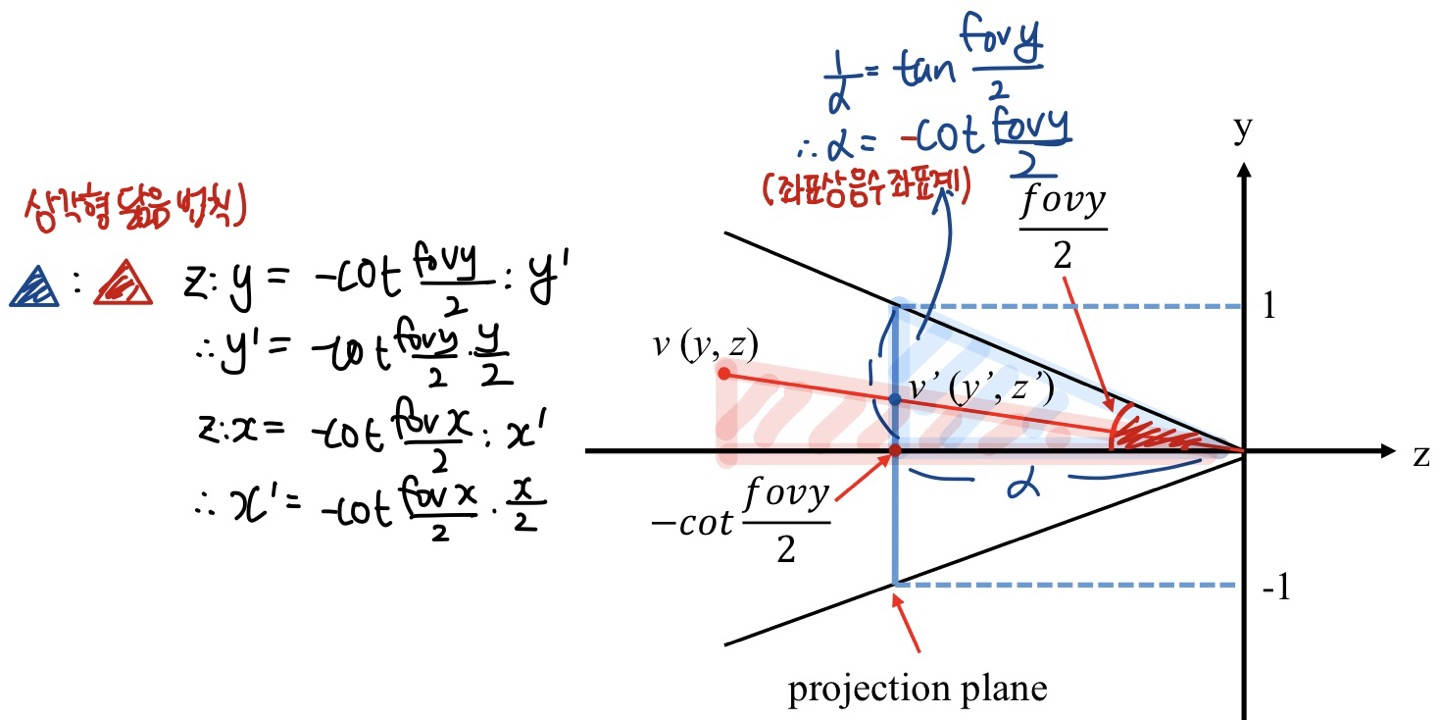
• y-z 좌표계 상에서 두 삼각형에 대해 닮음 법칙을 적용해서 y', x' 의 값을 구할 수 있습니다.

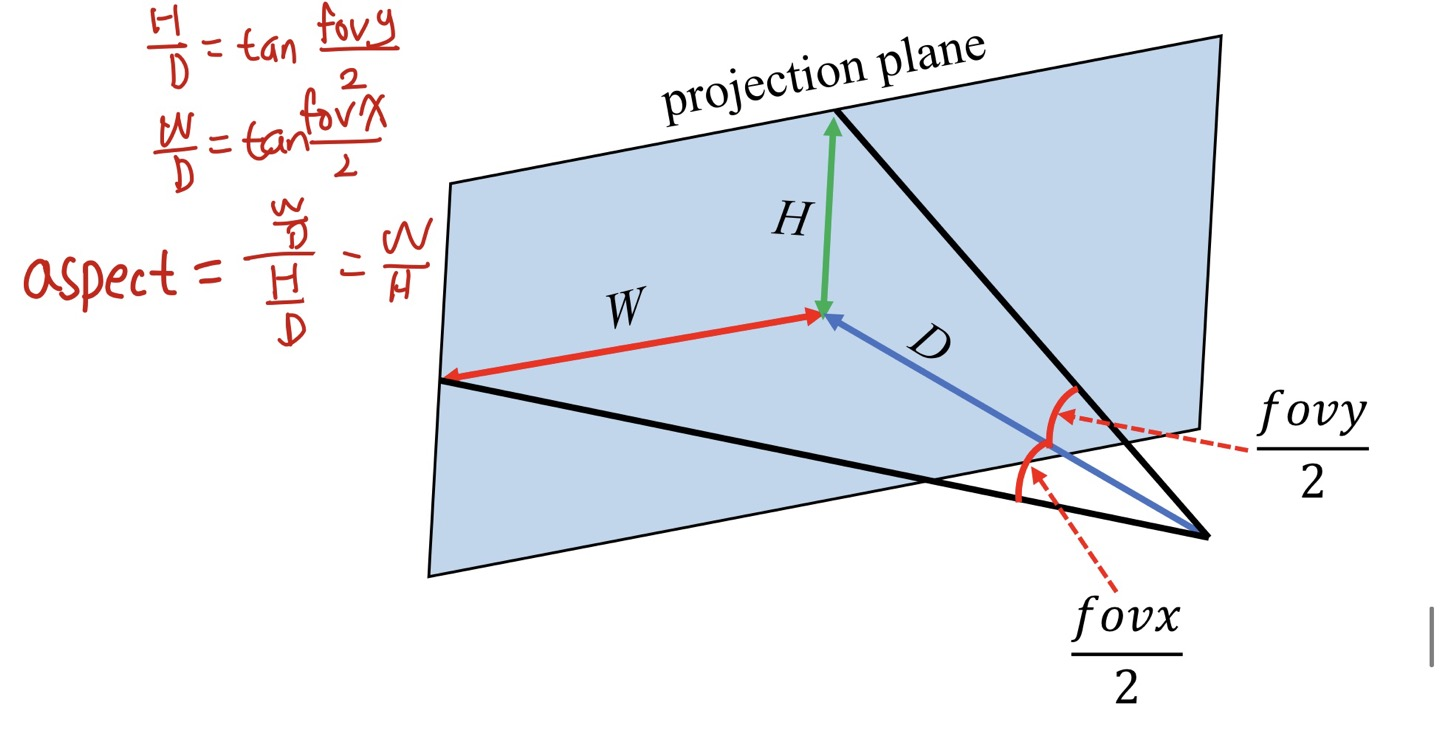
• 수식에 의해 transformed 된 지점의 좌표를 구할 수 있습니다.

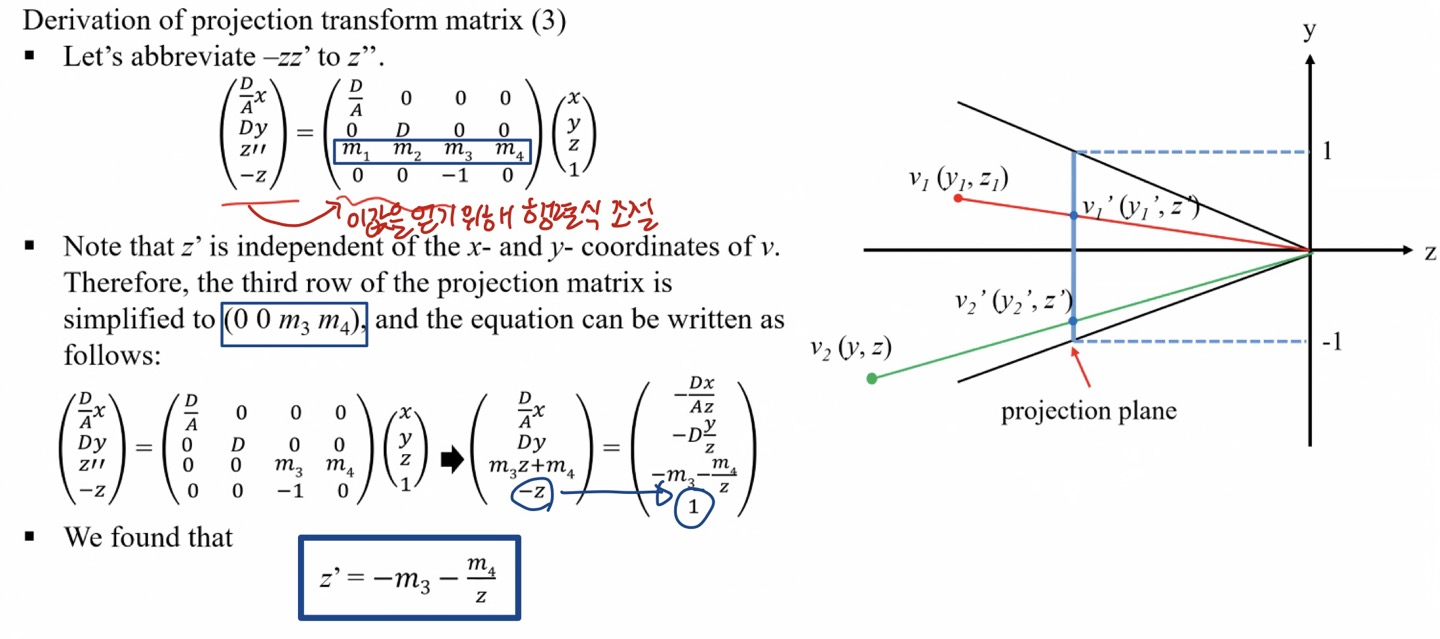
• 우리가 이미 알고 있는 상수값인 −f 값과 −n 값을 -1, 1에 매핑해서 연립방정식을 세우고 해를 구할 수 있습니다.

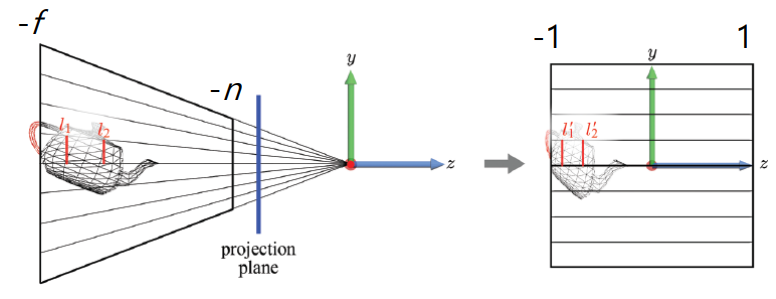
• 따라서 Projection Matrix 를 구할 수 있습니다.

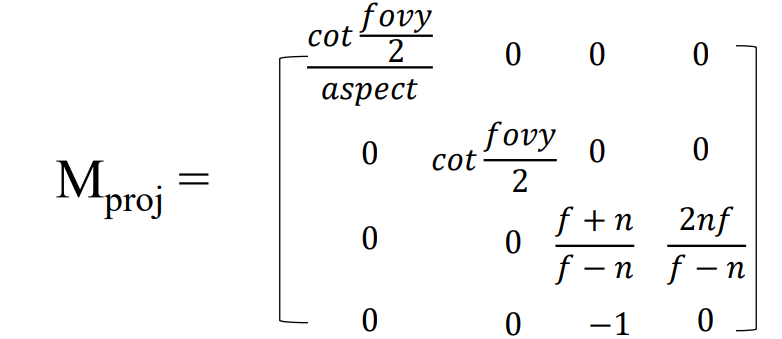
다시, Projection Transform

• 위에서 구한 Projection Matrix 를 이용해 view Frustum -> Cubic view volume 으로의 Projeciton Transform 이 이루어지는 것입니다.

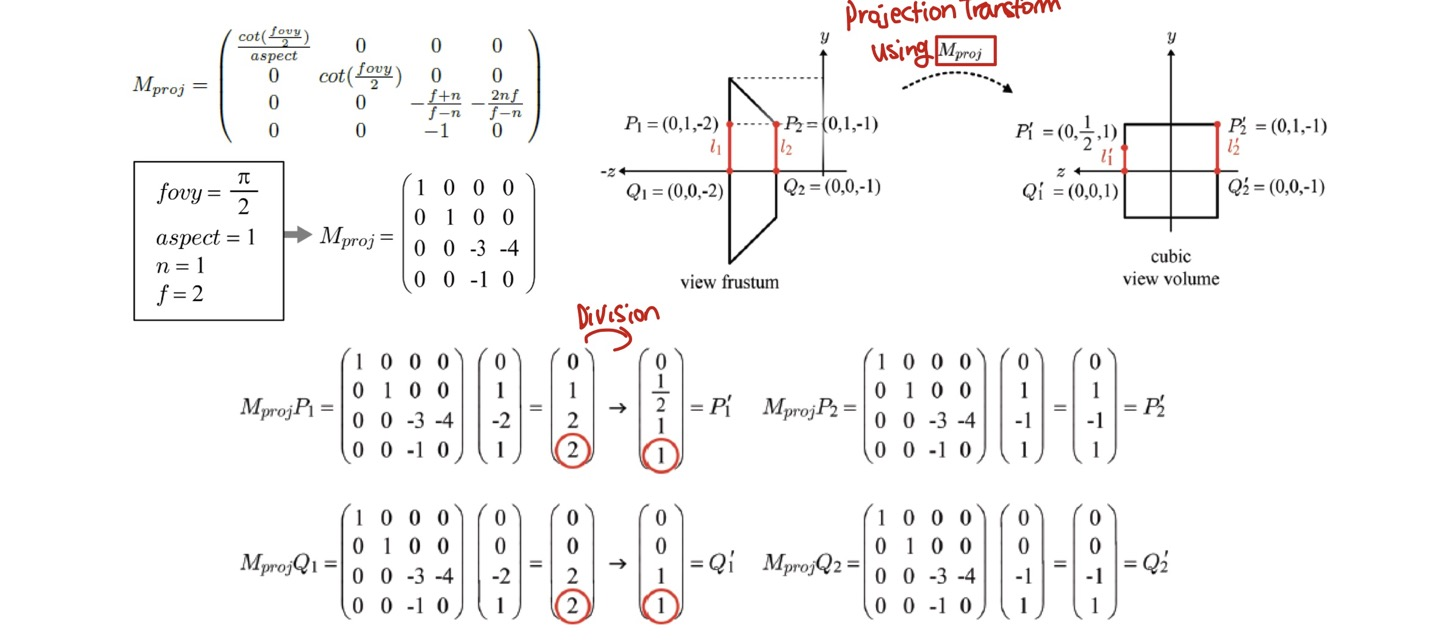
• 각 좌표에 M(proj)를 곱해 새로운 좌표를 얻을 수 있습니다.

Tessellation Stages

• Tessellation 은 주어진 메시의 삼각형들을 더 잘게 쪼개서 새로운 삼각형들을 만드는 과정을 말합니다. 새 삼각형들을 새로운 위치로 이동함으로써 원래 메시에 없는 세부적인 특징을 만들어 낼 수 있습니다.

• Tessellation 은 여러 장점이 있습니다.

  • 카메라에 가까운 삼각형들에는 테셀레이션을 적용해서 세부도를 높이고, 먼 삼각형들에는 Tessellation 을 적용하지 않는 방식의 세부 수준(Level-Of-Detail, LOD)을 구현할 수 있습니다. LOD 를 구현하면 관찰자가 실제로 볼 수 있는 부분에만 많은 삼각형을 사용하게 되므로 효율적입니다.
  • 적은 수의 삼각형들로 이루어진 메시를 메모리에 담아두고 즉석으로 삼각형을 추가하여 메모리를 절약할 수 있습니다.
  • 애니메이션이나 물리 처리 같은 연산들을 단순한 다각형 메시에 대해 수행하고, Tessellation 된 다각형 메시는 렌더링에만 사용함으로써 계산량을 줄일 수 있습니다.

• Tessellation 단계들은 꼭 필요한 단계가 아니기 때문에 생략이 가능합니다. 이제, 각 단계들을 살펴봅시다.

Hull Shader (HS) Stage

• Primitive 의 어디에 혹은 어떻게 Vertex 를 추가할지를 결정합니다. 그 후, 결정된 정보를 Tessellator stage 와 Domain shader stage 에 전달합니다.

Tessellator (TS) Stage

• Hull Shader 로부터 전달받은 정보를 바탕으로 실제로 primitive 를 나누는 작업을 수행하고, output 을 Domain shader 에 전달합니다.

Domain Shader (DS) Stage

• Hull Shader 로부터 전달받은 vertex 의 position 정보와 Tessellator 에서 만든 vertex 를 바탕으로 vertex 에 대한 transform 을 수행합니다.

Geometry Shader (GS) Stage

• Geometry Shader 단계는 선택적인 단계이기 때문에 생략이 가능합니다. 이는 하나의 기본 도형을 입력받아 그것을 임의로 변형합니다.

  • 예를 들어 삼각형 목록을 그리는 경우 기하 셰이더에는 삼각형을 정의하는 (Vertex Shader 단계를 거친) 정점 세 개가 입력됩니다.

• Geometry Shader 의 주된 장점은 기하 구조를 GPU 에서 생성하거나 파괴할 수 있다는 것입니다.

  • 예를 들어 입력 기하 구조를 여러 개의 기하 구조로 확장할 수도 있고, 조건에 따라 삭제할 수도 있습니다.
  • 기하 셰이더의 흔한 용도는 점이나 선분을 사각형으로 확장하는 것입니다.

• 또한 기하 셰이더의 출력은 바로 Rasterizer stage 에 넘겨줄 수도 있지만, 스트림 출력 단계를 통해 메모리의 버퍼에 저장해 두고 나중에 활용하는 것이 가능합니다.

  • 이는 고급 기법입니다.

Stream Output (SO) Stage

• Vertex 데이터를 얻기 위한 단계입니다.

  • 일반적으로 Geometry Shader 단계에서 수행되지만, Geometry Shader 가 없는 경우에는 Vertex Shader 단계에서 수행됩니다.

• Stream Output 은 Vertex 데이터를 얻어서 메모리에 전달하고, 전달된 데이터는 Vertex buffer에 저장됩니다.

• Triangle list, line list 등의 리스트 형태로 Vertex 데이터를 보내고, incomplete primitive 는 보내지지 않고 삭제됩니다.

  • incomplete primitive : two vertex triangle, one vertex line 등

• Particle Effect 를 생성하거나 제거하는데 유용하게 활용됩니다.

Rasterizer Stage (RS)

Preprocessing

• Rasterzer Stage 는 Vertex Shader 에서 얻은 vertex 의 wire 형태를 Pixel Shader 에서 색상을 입히기 전에 각 pixel(Fragments)을 생성시키는 역할을 합니다.

Clipping

• 앞서 Projection Transform 에서 Clipping 에 대해 잠깐 언급했었습니다.

  • View frustum 절두체의 경계에 있을 때 clipping 하는 것에 대한 내부 처리를 Rasterizer Stage 에서 적용할 수 있습니다.

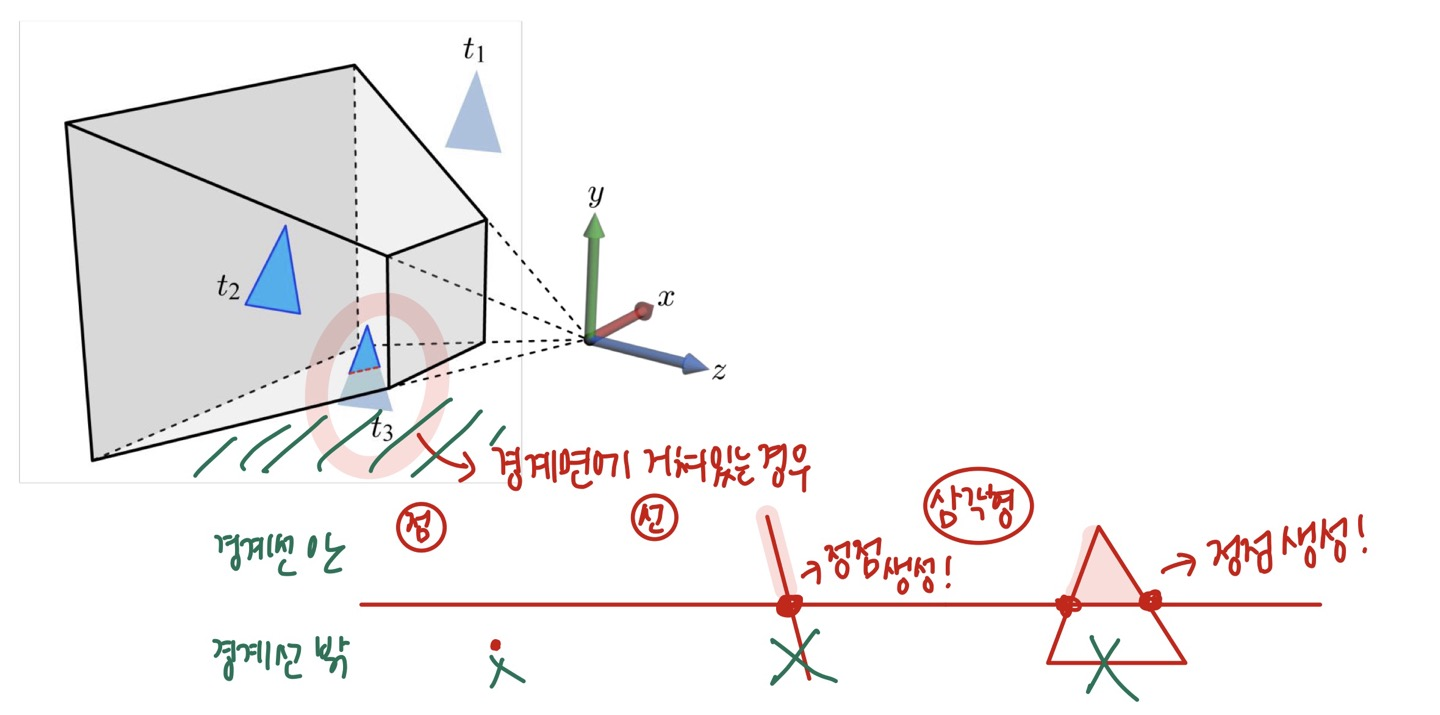
Perspective Division

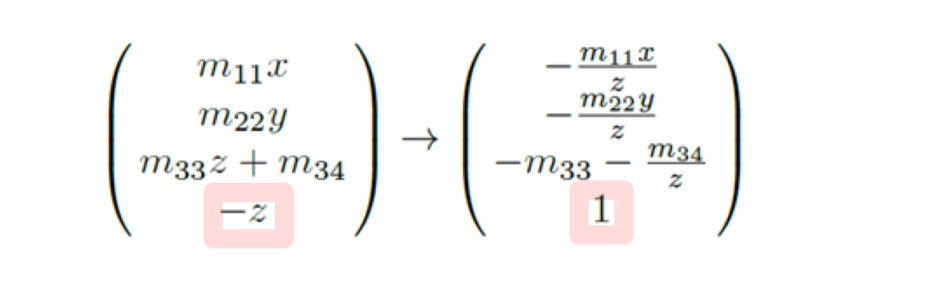
• M(proj)에서 w 좌표가 1이 아닌 −z 가 나오는 것을 볼 수 있습니다. 이 경우 각 항을 −z 로 나눠서 1로 바꿔줍니다.

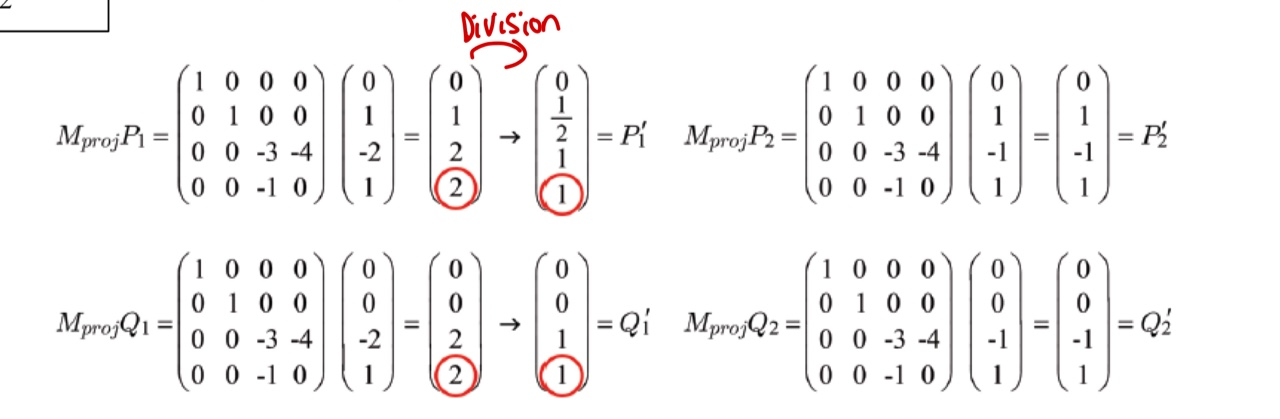
• 이를 나눠주어 w 좌표가 1이 된 결과의 좌표를 NDC(Normalized Device Coordinates) 라고 합니다.

• Perspective Division 을 하는 이유는 다음과 같습니다.

  • w 좌표는 동차 좌표로 이 값을 1로 두면, 다른 xyz 값에 대해서도 제대로 길이를 맞춰줄 수 있습니다.
  • Perspective Division 을 통해 제대로 원근법이 적용되는 것을 확인할 수 있습니다.

Viewport Transformation

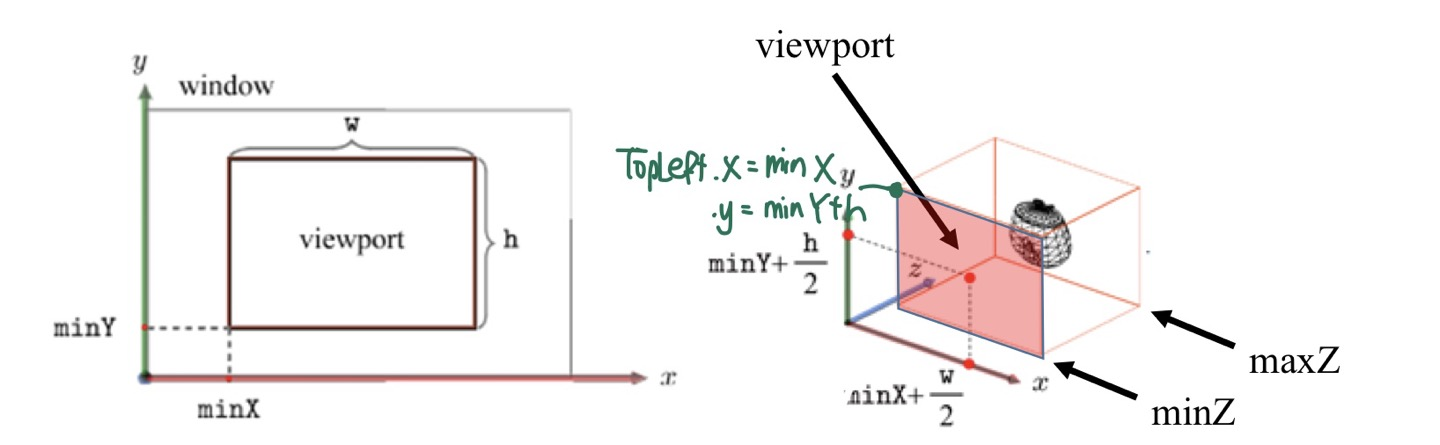
• Clip NDC Space 의 cube(Perspective division 이 이루어진 상태)를 우리의 모니터 상에서의 창으로 옮겨줘야 합니다.

  • 이때 viewport 를 이용합니다.

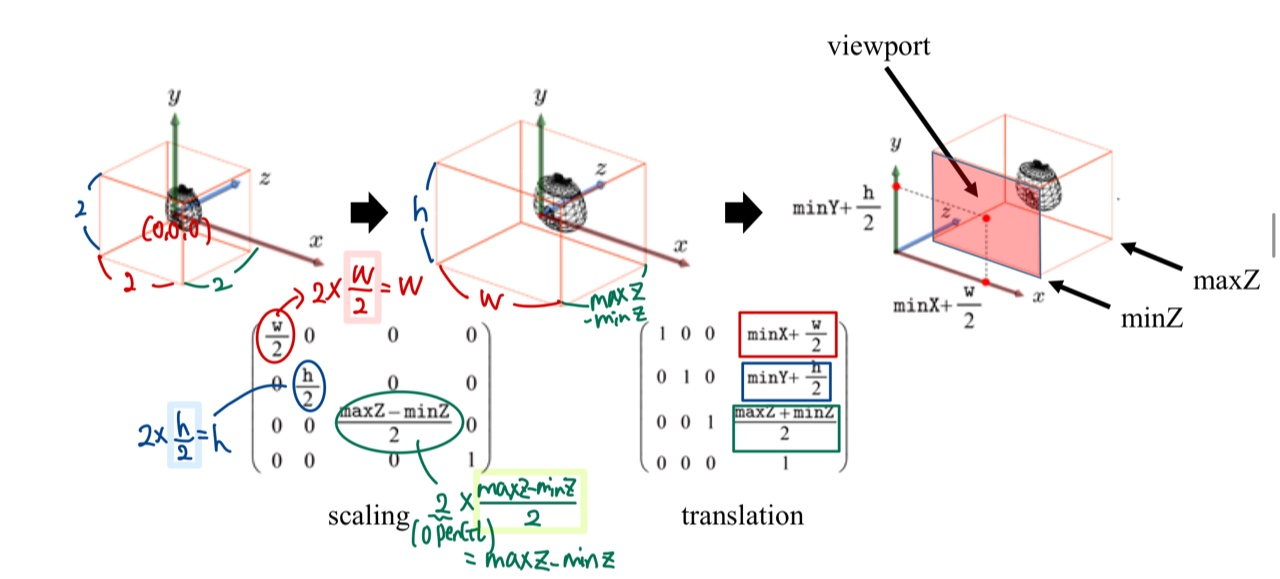
• 각각 Scaling, Translation 변환 행렬을 구할 수 있습니다. 또한 두 행렬을 Affine 행렬으로 합쳐서 정의할 수 있습니다.

Face Culling

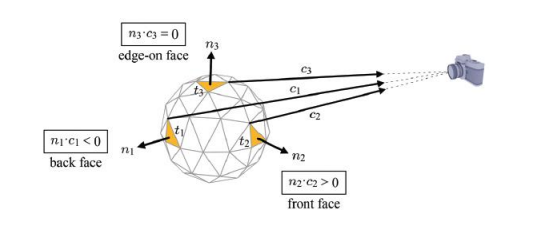
• 카메라가 관측하지 않는 공간(Back face)에 대해 연산을 하지 않는 것을 의미합니다.

  • 하나의 삼각형에 대해 3개의 vertex 와 이를 채우는 fragment 들은 100개가 넘습니다. 이런 무거운 연산을 줄이기 위한 방법입니다.

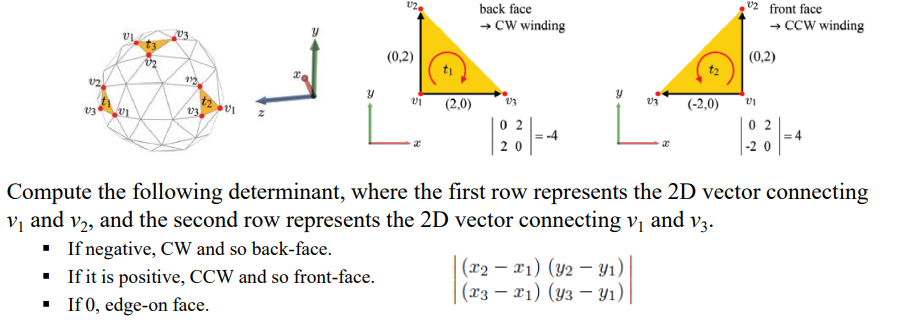
• Face 가 BackFace 인지, FrontFace 인지는 winding 의 방향을 알면 알 수 있습니다.

• 행렬식의 부호를 알면, 일일이 face 의 winding 을 알지 않아도 해당 face가 CW, CCW 인지 알 수 있습니다.

• back face culling 이 항상 이뤄지는 것은 아닙니다.

  • global illumination 등 보이지 않는 간접적인 영역에 대해 계산이 필요한 경우에는 back face 도 연산을 해주어야 합니다.

Processing

• 본격적으로 픽셀을 채우는 단계입니다.

Edge Equation

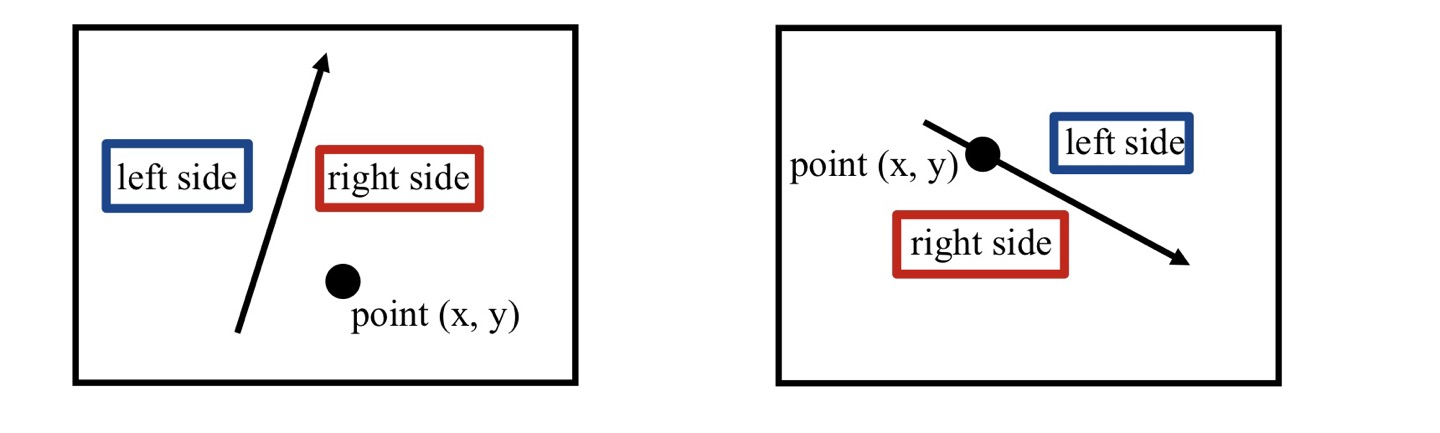
• Edge Equation 은 직선이 주어졌을 때 pixel 이 어느 편에 존재하는지 적용시킬 수 있습니다.

  • right : positive number
  • left : negative number
  • on the line : zero number

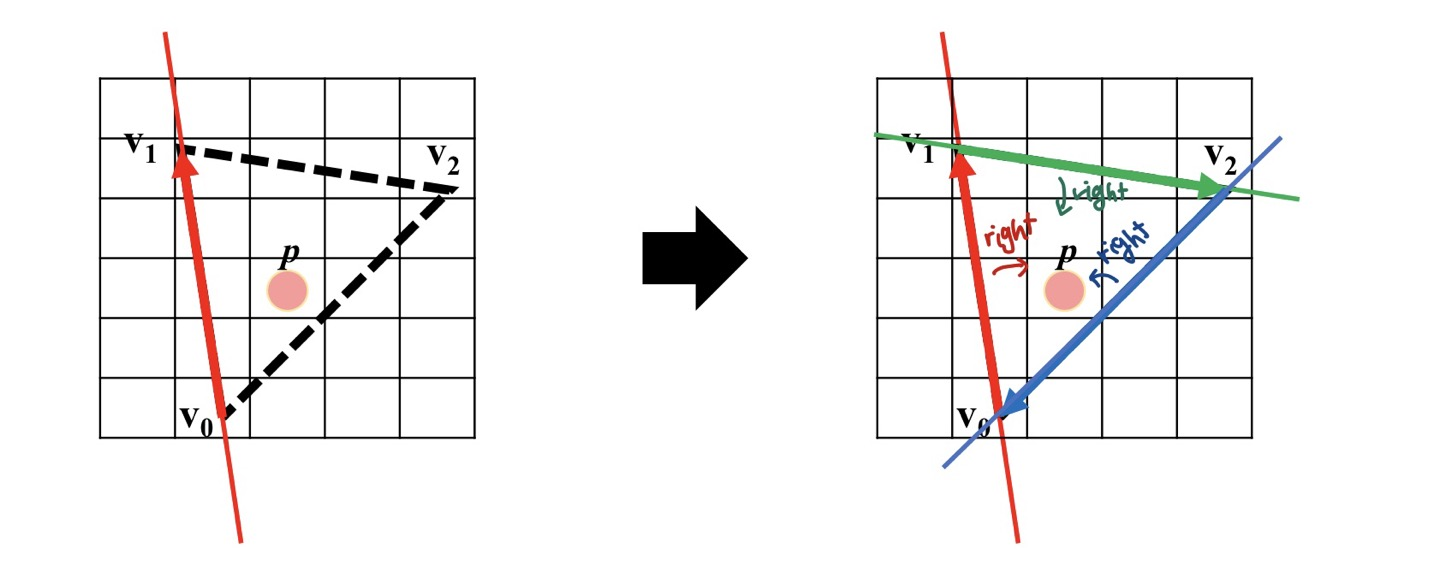
• 즉, Egde Equation 으로 pixel 이 삼각형 내부에 있는지, 아닌지 판별할 수 있습니다.

  • 해당 삼각형의 내부의 픽셀 p 의 경우 모든 직선의 오른쪽에 존재하기 때문에 해당 pixel 은 삼각형 내부에 존재하는 픽셀입니다.
  • 이 경우, edge funtion 은 3개의 edge 에 대해 positive number 을 return 합니다.

Definition of Edge Equation

• 그렇다면 Edge Equation 식의 정의는 무엇이고, 어떻게 부호에 따라 pixel 의 위치관계를 결정할 수 있는지 알아보도록 합시다.

• 우선 벡터 v0p 와 v0v1 의 외적을 구해봅시다.

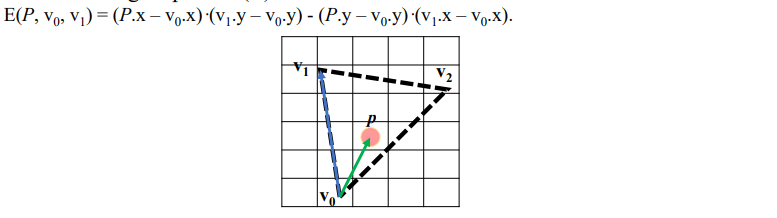
• 외적으로 새로 생기는 벡터의 부호에 따라 pixelpoint 의 위치 관계를 알 수 있습니다.

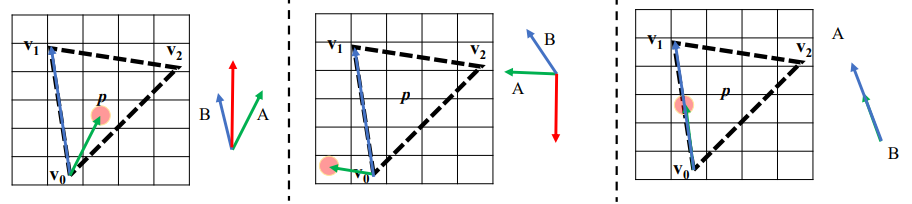
• 위의 그림과 같이 A 벡터의 위치가 각각 다를때,

  • 외적의 부호가 양수이면, pixel 은 오른편에 존재합니다.
  • 외적의 부호가 음수이면, pixel 은 왼쪽에 존재합니다.
  • 외적의 부호가 0이면, pixel 은 동일한 선상에 존재합니다.

• 이를 기하하적 의미로도 해석할 수 있습니다.

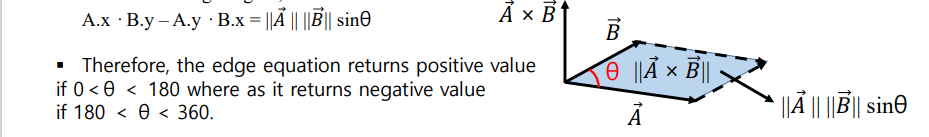
Assigning Atrributes for Fragments

• Vertex Shader 에서는 Vertex 의 position, RGB, Normal 등의 값을 cpu 에서 gpu 로 넘겨주었습니다.

• 하지만, fragment 에 대해서는 따로 전달해주는 것이 없기 때문에 이를 할당해주어야 합니다.

  • 즉, 이미 가지고 있는 정보들을 가지고 결정할 수 있도록 하는 단계가 필요합니다.
  • 이를 Interpolation 이라고 합니다.

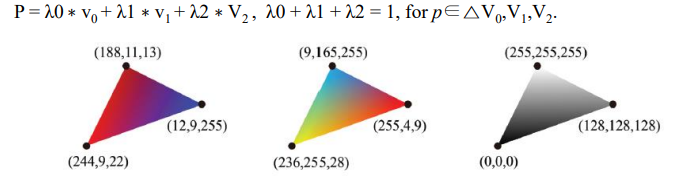
• Vertex Shader 에 들어온 vertex Position 과 RGB 색상 정보등을 가지고 fragment 의 position, RGB 에 가중치를 두어서 결정할 수 있습니다.

  • 각 가중치의 총합은 λ0 + λ1 + λ2 = 1 입니다.

• 삼각형 내부의 pixel p 는 3개의 vertex 에 대해 각 가중치 비율에 따라 RGB 좌표를 곱해서 나타낼 수 있습니다.

  • P = λ0 ∗ v0 + λ1 ∗ v1 + λ2 ∗ v2 으로 나타낼 수 있습니다.

Barycentric Coordinate

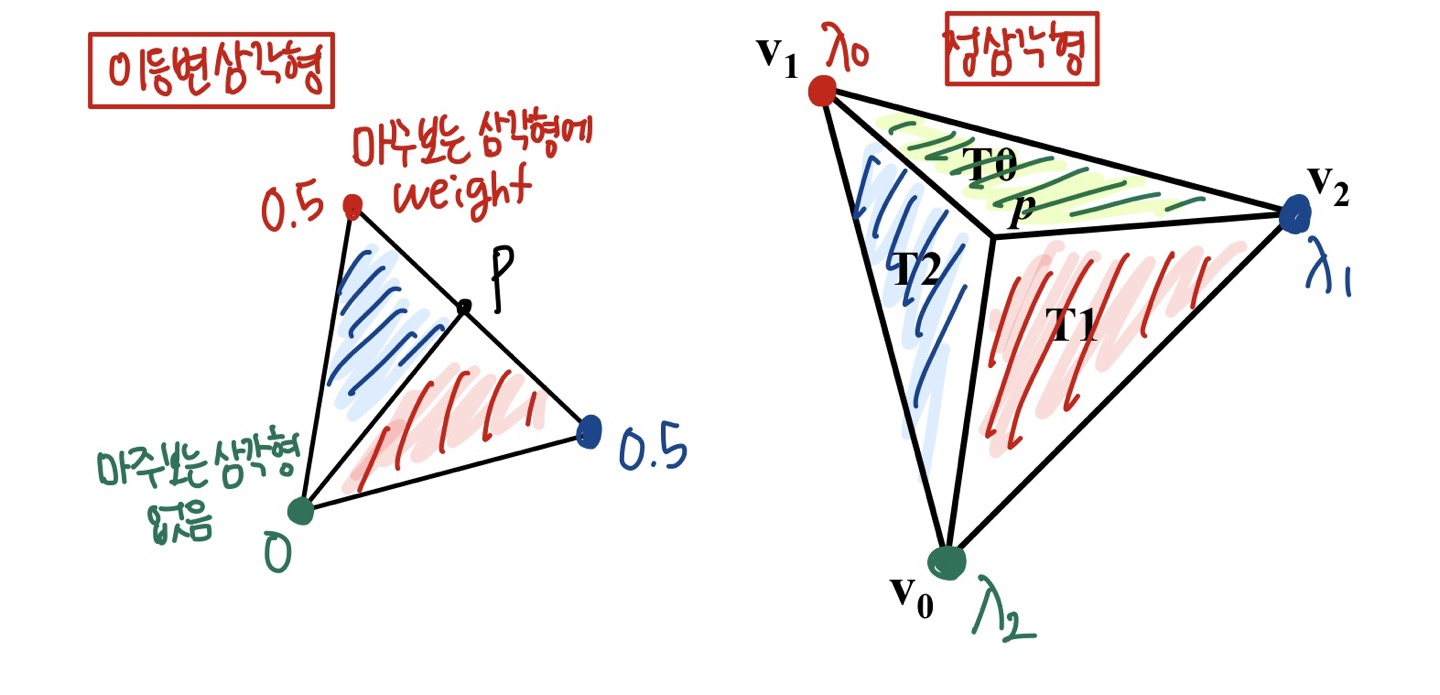
• 삼각형 내부의 pixel p 의 위치에 따라서 가중치 값을 다르게 가집니다.

• 각 가중치 좌표 (λ0, λ1, λ2)은 삼각형 (T0, T1, T2)를 마주보며 가중치 값을 가집니다.

• 삼각형의 면적은 두 벡터를 외적한 크기, 즉 평행사변형의 면적이므로 이를 2로 나눠줍니다.

  • T0 의 경우 0.5 ∗ E(p, v1, v2) 로부터 삼각형 면적을 구할 수 있습니다.
  • T1 의 경우 0.5 ∗ E(p, v2, v0) 로부터 삼각형 면적을 구할 수 있습니다.
  • T2 의 경우 0.5 ∗ E(p, v0, v1) 로부터 삼각형 면적을 구할 수 있습니다.

• 가중치는 총합이 1이므로 전체 넓이 대비 자신의 weight 가 가지는 부분 면적의 비로 나타낼 수 있습니다.

Fragments color 값 계산

• 위의 내용을 바탕으로 삼각형 내부의 pixel p 의 위치에 따라서 가중치 값을 다르게 가지는 color 를 결정할 수 있습니다.

Pixel Shader (PS) Stage

• 화면 안에 보일 각 pixel fragment 에 대해 조명, 반사, 그림자 효과 등 더 복잡한 작업을 수행하여 최종 색상을 결정하는 것입니다.

  • pixel fragment 란 화면 안에 그려질 잠재적인 픽셀을 말합니다.

• Rasterizer Stage 에서는 각 픽셀 당 한 번씩 Pixel Shader 를 호출합니다.

  • Vertex Stage 와 비슷하게 하나의 pixel 을 받아서 하나의 pixel 을 리턴합니다.

Output Merger (OM) Stage

• pixel fragment 와 depth/stencil buffer 를 받아서 실제로 그려질 픽셀을 결정합니다.

  • 설정에 따라 blending 을 적용하기도 합니다.

• Pixel Shader 가 생성한 pixel fragment 들은 Output Merger 단계로 입력됩니다.

  • 이 단계에서 일부 pixel fragment 들이 깊이 혹은 stencil 판정에 의해 삭제될 수 있습니다.

• 삭제되지 않은 pixel fragment 들은 Back buffer 에 기록됩니다.

  • Blending 도 이 단계에서 일어납니다. 이는 새 pixel 이 Back buffer 의 기존 pixel 을 완전히 덮어쓰는 것이 아니라 두 pixel 을 일정한 공식에 따라 섞은 결과를 기록하는 것을 말합니다.
  • Blending 은 반투명과 같은 특수 효과를 내는 데에 쓰입니다.

Introduction

• Output merger Stage 에서 pixel 들의 최종 color 를 결정하는데 다음의 과정이 필요합니다.

  • pipeline state
  • pixel shader stage 에서 return 한 pixel (texturing, lighting) 데이터
  • render targets
  • depth/stencil buffers

Render target

• 최종적으로 그려지는 buffer 가 아닌 임시 메모리 buffer 에 그린 후 최종 GPU 에 넘길 buffer 로 전달해주는 역할을 합니다.

Back buffer/Frame buffer

• Frame Buffer : 최종적으로 그려지는 buffer 중 송출되고 있는 buffer 입니다. RAM 에 저장된 최종 color data 들이 저장되어 있습니다.

• 최종적으로 그려지는 buffer 중 실제 완성되어 송출되기 전에 미리 뒤에서 그려놓고 업데이트 시켜주는 역할을 하는 버퍼가 Back buffer 입니다.

Depth-Stencil Testing

• 위의 그림을 보면 초록색 삼각형과 파란색 삼각형은 꼬인 위치의 관계를 가져 한쪽은 초록색이 위로, 다른 한쪽은 파란색이 위에 놓여있도록 렌더링됩니다.

  • pixel shader 에서 받아온 각각의 삼각형에 대해서 누가 더 앞에 있는지 판단해서 그릴 부분과 그리지 않는 부분을 처리하는 것이 Depth-Testing 입니다.

• 위의 그림과 같이 0과 1로 나타난 데이터에서 1로 된 영역에만 렌더링을 진행합니다.

  • pixel shader 에서 받아온 오브젝트에 대해 stencil 로 지정된 영역을 통과하는 픽셀만 렌더링해주도록 처리하는 것이 Stencil-Testing 입니다.

• Depth, Stencil 모두 Output-Merger 단계에서 픽셀을 그릴 것인지 그리지 않을 것인지 결정하는 것입니다.

Depth test

• Pixel shader 에서 받아온 각각의 삼각형에 대해서 누가 더 앞에 있는지 판단하는 버퍼를 depth buffer 라고 부릅니다 (z - buffering).

• Output-merger 단계에서 depth 값이 들어오면 viewport 내부로 clamp 됩니다.

• z = min(Viewport.MaxDepth, max(Viewport.MinDepth,z))

• 즉, viewport의 최소 깊이와 z 버퍼의 깊이를 먼저 비교해서 고정을 시키고, viewport의 최대 Depth 값보다는 작도록 z 값을 결정합니다.

Depth Test Stage

• 우선 Depth 는 per-sample operation 이 이루어집니다.

• 어떤 오브젝트가 screen 에 projection 될 때, 생성된 pixel 과 현재의 depth buffer 값의 비교를 통해 생성된 pixel 의 depth 를 결정합니다.

  • 이때, depth 가 더 깊은 픽셀들이 생성된 경우는 draw 하지 않고 작은 경우에는 현재의 버퍼에 새로 생성된 depth 를 버퍼에 update 하는 것입니다.
  • 즉, existing 한 값과의 비교를 통해 결정하는 것입니다.

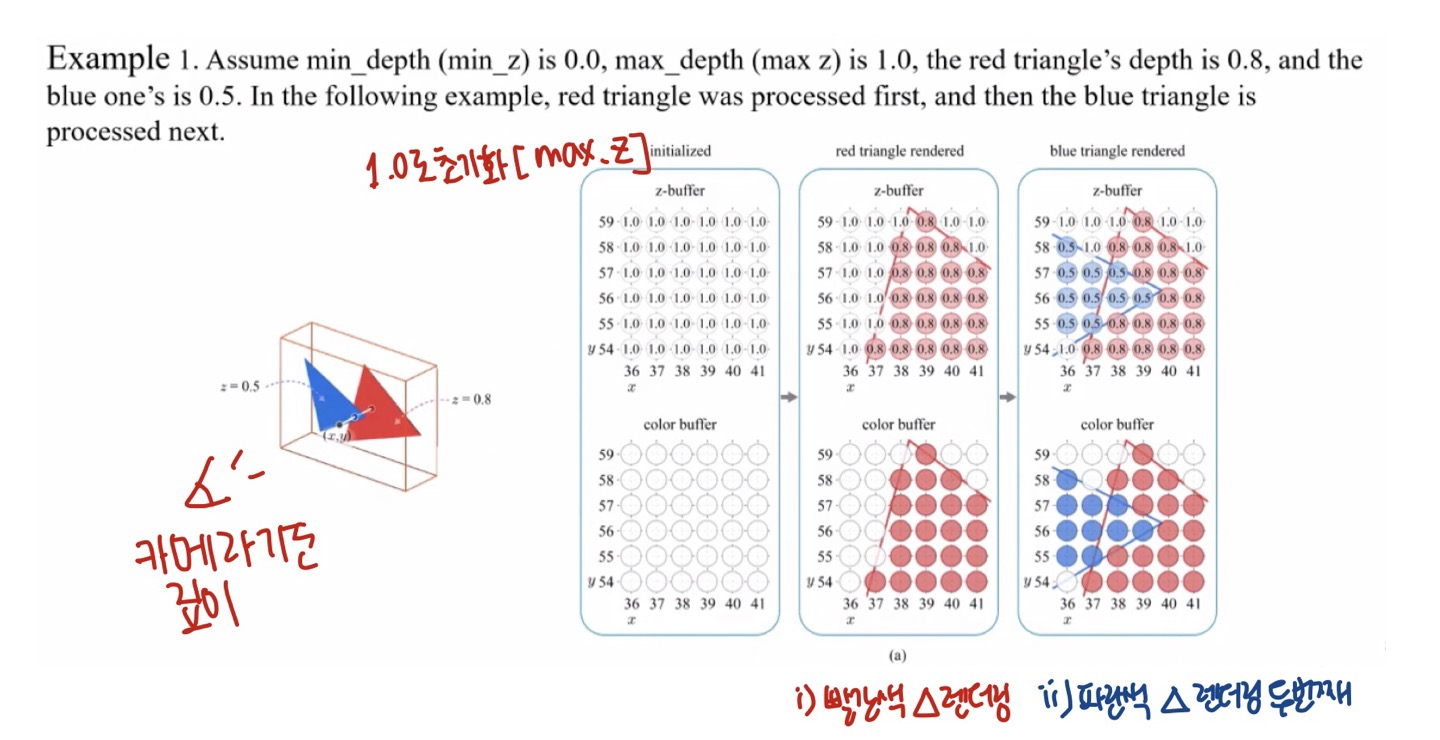
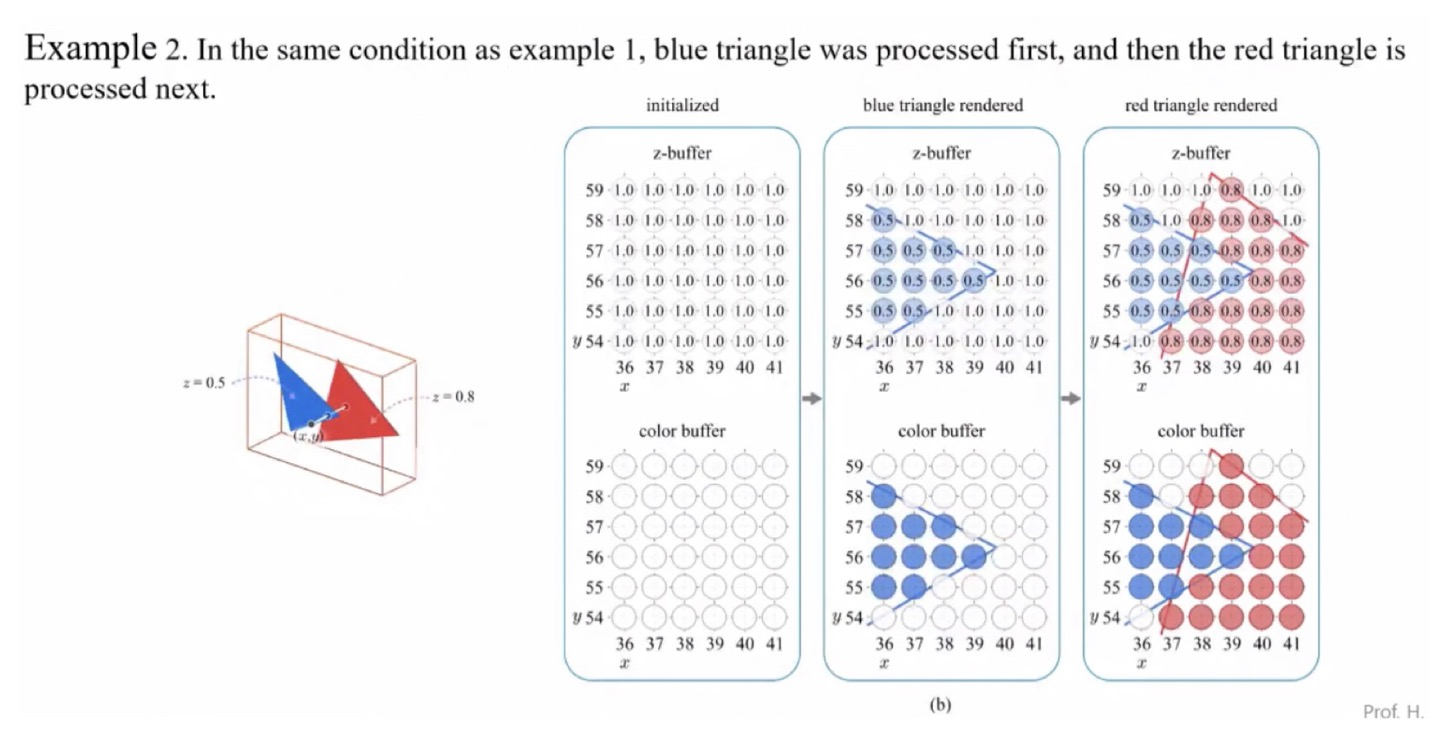
• 위의 Depth Test 과정을 예시로 들어 설명할 수 있습니다.

다시, Depth-Stencil Testing

Transition Effect

• 한 scene에 두 개의 텍스쳐를 겹쳐서 렌더링할 때, 두 개를 모두 렌더링할 수 도 있지만 이럴 경우 보이지 않게 되는 부분에 대해서도 연산이 필요하기 때문에 비효율적입니다.

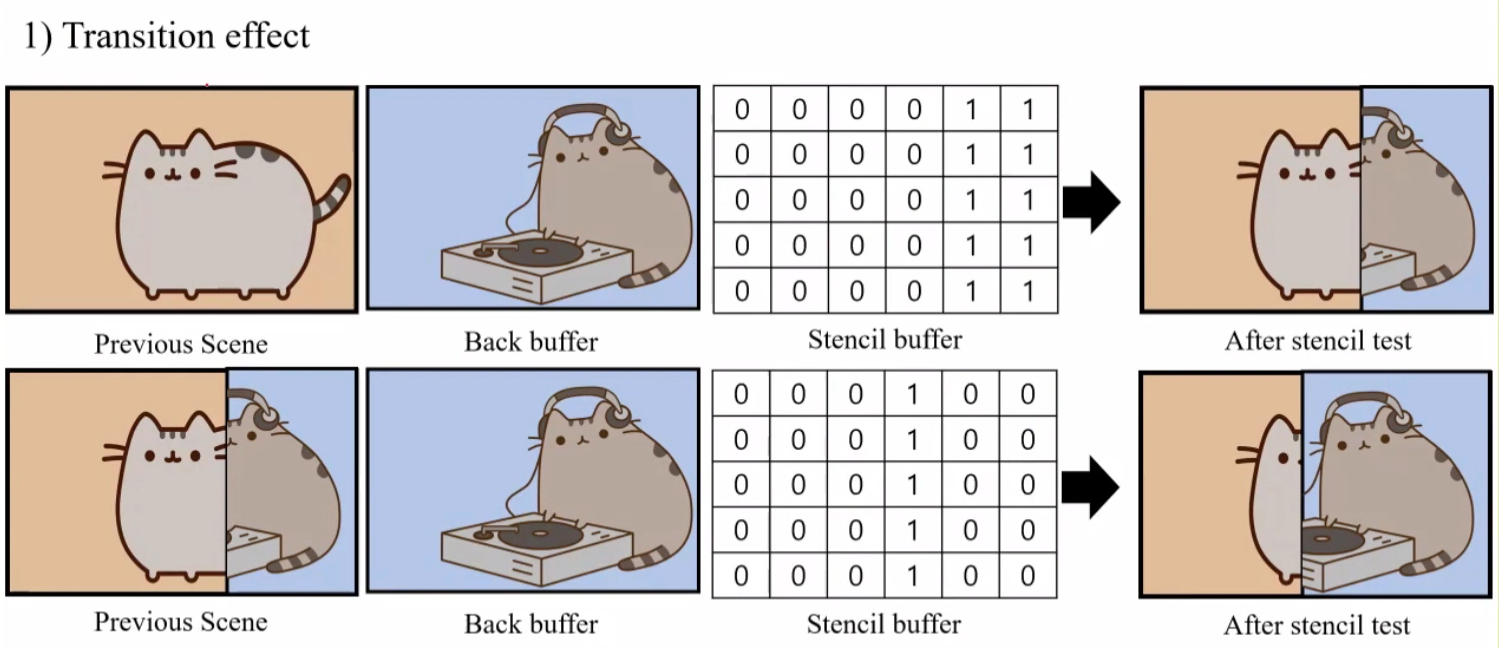
• 따라서 stencil test 를 통과한 buffer 값에 대해서만 update 시켜줄 수 있습니다.

Discarding UI area

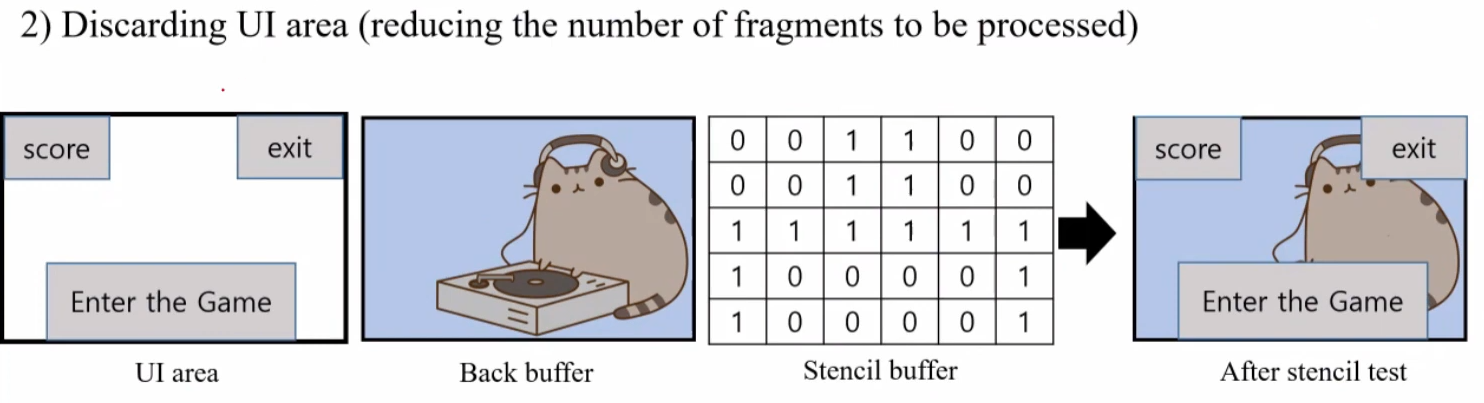
• UI 의 경우에는 행동이 변하지 않기 때문에 계속 렌더링을 시켜주는 것이 비효율적입니다.

  • 따라서 해당 area 의 경우 stencil 로 update 할 영역에서 UI 를 빼서 통과하지 못하게 만들어 update 시켜주지 않습니다. 그렇게 되면 UI 를 제외한 나머지 영역만 통과되어 update 하게 됩니다.

Color Blending

• 지금까지 Depth-Stencil 로 겹치는 부분에 대해서 무엇을 앞에 그릴 지를 결정해주었습니다. 하지만 오브젝트의 투명도를 고려해줄 때 문제가 발생할 수 있습니다.

  • 따라서 Color Blending 을 통해 최종 pixel color 를 혼합해서 결정해줍니다.

• color blending 이 이루어지는 시기는 render target 에 들어가기 전에 결정됩니다.

• Output Merger 단계에서 render target 을 이용하여 최종 buffer 로 전달하였는데, color blending 에서 어떤 색깔을 blending 할지에 대한 값은 render targe 에 들어가기 전에 결정된다는 것입니다.

  • 즉, 최종 buffer 에 기록되는 것이 아니라 render target 에 기록됩니다.

Blending Equation

• c = αc(f) + (1−α)c(p)

  • c : blending color, 최종 color
  • α : pixel's opacity
  • c(f) : fragment color, 새로 쓰여진 값 (αcf)
  • c(p) : pixel color, 기존 (1−α)c(p)

• opacity는 0~255의 값을 가지는데, 0인 경우 fully transparent하고, 255인 경우 fully opaque 합니다.

• [0,255]를 정규화시켜 [0,1] 로 나타낼 수 있습니다.

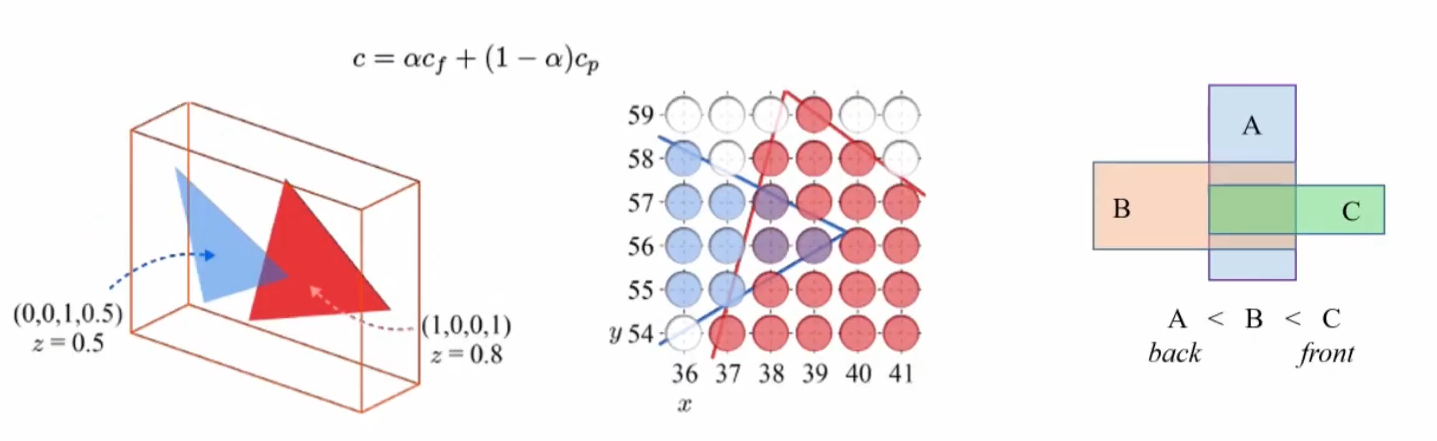
• primitive 는 먼저 불투명한 primitive 를 렌더링한 다음에, back-to-front 순서로 transparent 한 primitive 를 고려합니다.

  • 따라서 반투명한 오브젝트에 대해 순서를 정해주어야 합니다.

• 위의 그림과 같이 먼저 α 값이 1인 빨간색 삼각형, 즉 불투명한 primitive 에 대해 먼저 pixel 을 채웁니다. 그 다음에 α 값이 0.5인 파란색 삼각형을 그 위에 blending color 를 연산해서 채워줍니다.

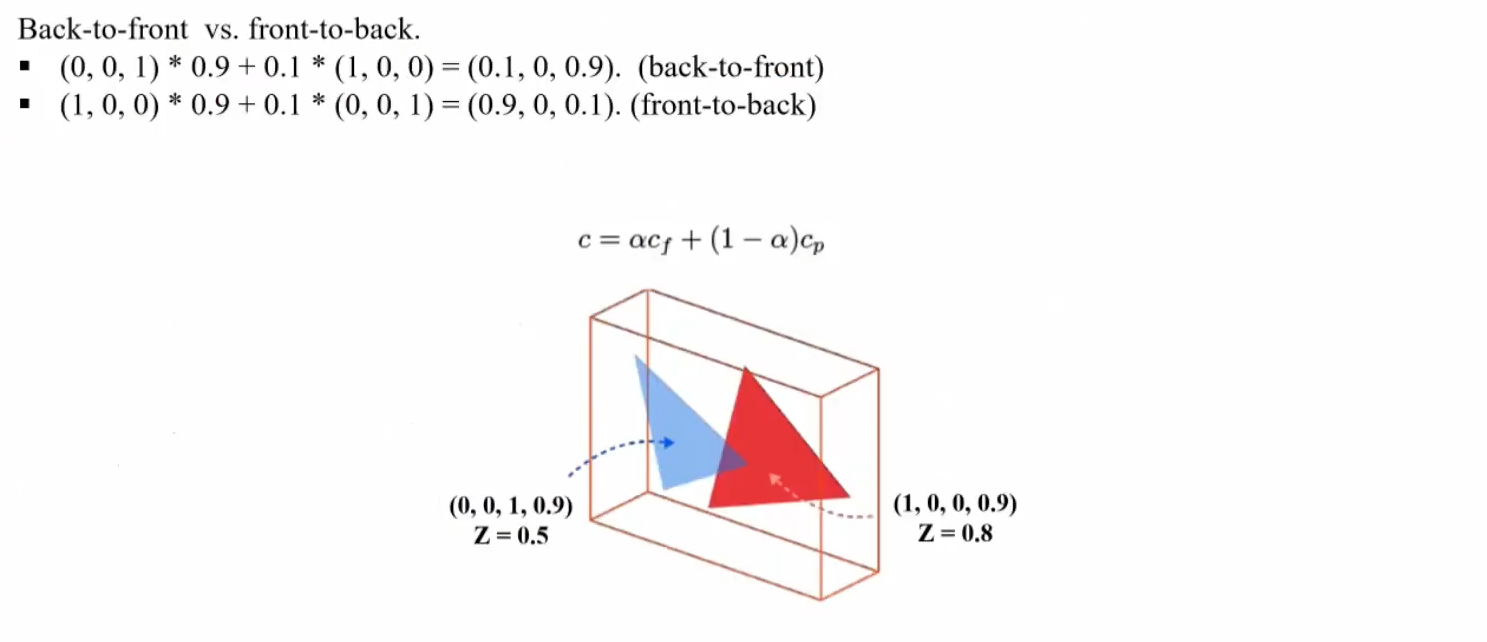
• 순서에 따라 다른 blending color 값을 가지는 것을 알 수 있습니다.

1. Transparent Or Opaque

• 가장 우선 순위는 Opaque 한 primitive 입니다. 이를 먼저 렌더링해줘야 합니다.

2. Depth - Z 값

• 현재 Z 값이 0.8인 빨간색 삼각형이 Z 값이 0.5인 파란색 삼각형 보다 더 먼저 렌더링됩니다.

3. Blending - α 값

• blending 을 해줄 때에는 Back 순서의 빨간색 삼각형에서 Front 순서의 파란색 삼각형 순서로 Blending Equation 을 풀어 blending color 값을 얻게 됩니다.

  • (1,0,0)의 값에 (1-α) = 0.1 를 곱해주어, 0.1 ∗ (1,0,0) 으로 color 값을 얻고 여기에 위에 생기는 (0,0,1) ∗ 0.9에 더해주면 최종 컬러가 나옵니다.

Reference

• Initializing DirectX 12
• [3D] 그래픽스 파이프 라인
• 렌더링 파이프라인
• 렌더링 파이프 라인? (Rendering Pipeline)
• Tessellation phase
• 파이프라인 (Pipeline)
• DirectX 그래픽스 파이프라인 순서 및 기본 설명과 기본 지식
• 렌더링 파이프라인(rendering pipeline)
• [GPU] 그래픽스 파이프라인 (Graphics Pipeline)
• 3D 그래픽스 - 그래픽스 파이프라인이란? (Graphics Pipeline)
• [DirectX 12] - Graphics Pipeline - 1
• [GG2022] Vertex Processing 이론