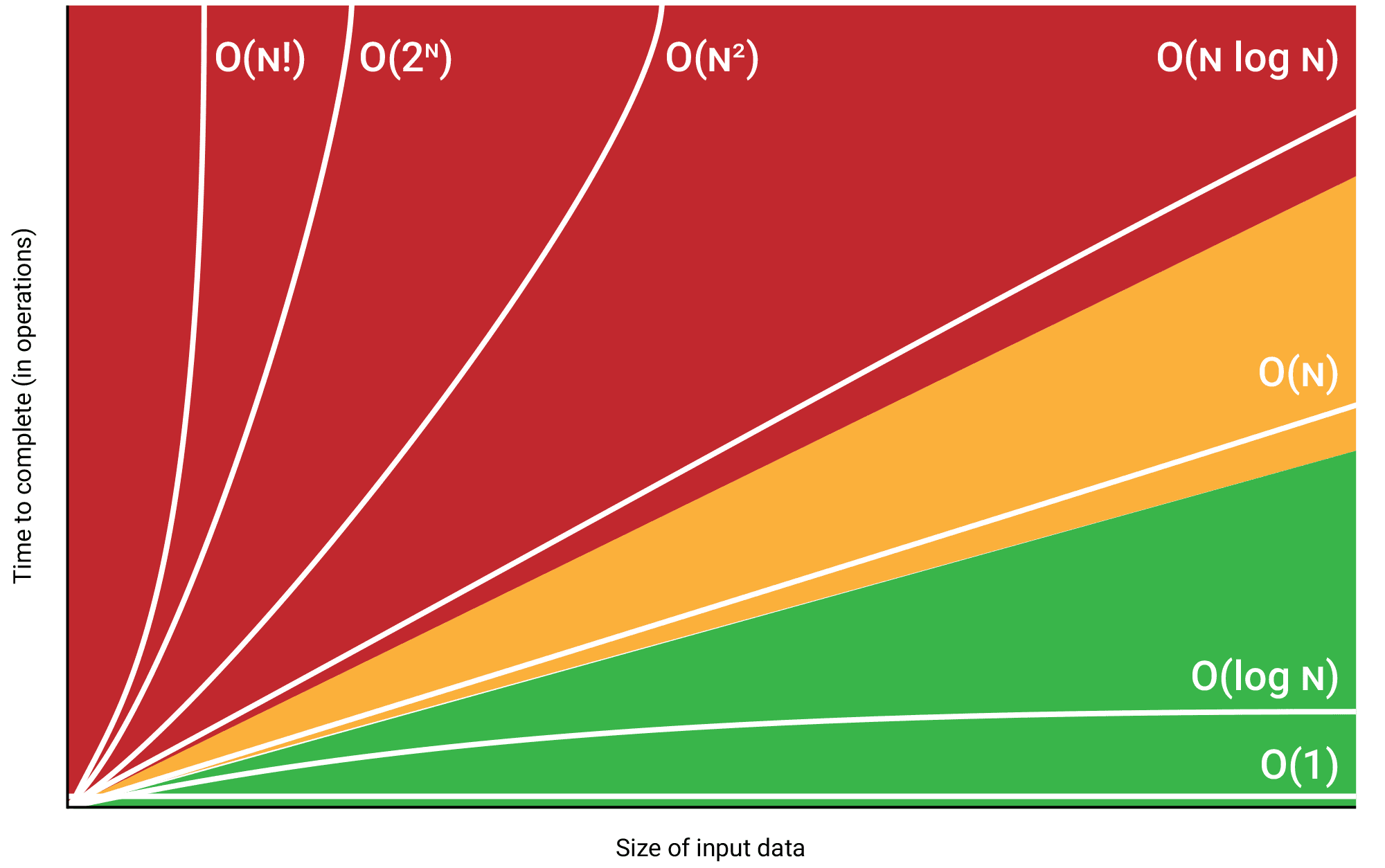
백준 코딩테스트 문제를 풀다가 시간복잡도 관련한 내용을 마주하고 많이 당황했었다. 그래서 이번일을 계기로 시간복잡도와 관련된 내용을 정리해보려고 한다.

시간복잡도

함수를 실행햇을 때 실행시간이 어느정도일지 표현하고 싶다
-> 실행시간이란 함수/알고리즘 수행에 필요한 스텝 수

알고리즘 스피드의 표현법
-> 빠르다, 느리다는 시간으로 표현하지 않는다
-> 걸리는 시간은 하드웨어가 결정하기 때문

따라서 알고리즘의 스피드는
- '완료까지 걸리는 절차의 수'로 결정

시간 복잡도란?

• 함수의 실행 시간을 표현하는 것. 주로 점근적 분석을 통해 실행 시간을 단순하게 표기하며, 이 때 점근적 표기법으로 표현

점근적 표기법?

위에서 시간 복잡도를 점근적 표기법으로 표현한다 하였는데 이것은 무엇일까?

점근적 분석(Asymptotic analysis)

• 임의의 함수가 N -> ∞ 일 때 어떤 함수 형태에 근접해지는지 분석

대표적으로 사용하는 점근 표기법은 3가지로

• O(Big O) 표기법: 알고리즘 성능이 최악인 경우(수행 시간의 상한)를 나타낼 때 사용
• Ω(Big Omega) 표기법: 알고리즘의 성능이 최선인 경우(수행 시간의 하한)를 나타낼 때 사용
• Θ(Big Theta) 표기법: 알고리즘이 처리해야 하는 수행 시간의 상한과 하한을 동시에 나타냄

이 중에서 최악의 경우에 대한 알고리즘 수행 시간이 가장 쓸모가 많다 보니 가장 많이 사용하는 알고리즘 성능 표기법으로 빅 O 표기법이 꼽힌다.

Big-O 표기법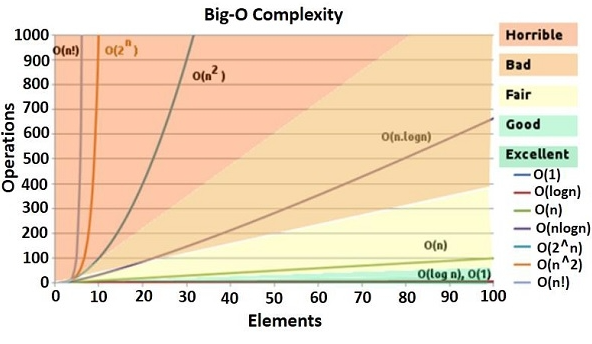

그렇다면 가장 많이 쓰인다는 Big-O표기법에 대해 알아보자

기본적으로 Big-O표기법이란 알고리즘의 효율성을 표기해주는 표기법이다

특징

• 상수는 무시한다
• 영향력 낮은 계수와 낮은 차수의 항은 무시한다
• 시간복잡도를 빠르게 설명할 수 있게된다
• 읽기 쉽고 바로 설명이 가능하다
• 알고리즘 분석을 빠르게 할 수 있고, 언제 무엇을 쓸지 빠르게 파악할 수 있다
• 본인의 코드를 평가도 할 수 있다

이런 장점을 가지고 있는데, 실제 사용을 예시를 통해 알아보자.

상수시간

def print_first(arr);
     print(arr[0])

• 배열의 첫 번째 인덱스를 출력하는 함수로, 단 한번만 수행된다.

• 입력으로 어떤 값이 들어와도 해당 함수는 단 한 번 수행되기에 이 함수의 시간복잡도는 상수시간이라고 할 수 있다
  -> 시간 복잡도: O(1)

• 그럼 함수 내에서 print를 두 번하게 만들면 시간 복잡도는 O(2)일까?
  -> 아니다. 동일하게 O(1)이라고 표현한다. BigO는 함수의 디테일에 관심이 없기 때문이다
  -> BigO는 큰 원리에만 관심이 있다. (인풋사이즈의 크기에 따라 어떻게 이 함수가 동작하는지)
  -> BigO는 상수에 신경을 쓰지 않는다!

선형 시간

def print_all(arr):
      for n in arr;
           print(n)

• 각 아이템을 다 프린트하는 함수
• 배열 사이즈가 10이라면 10번 수행되며, 배열이 100이라면 이는 100개의 스텝으로 이어질 것 이다.
• 배열의 크기가 커지면, 필요 스텝도 커진다
  -> 시간 복잡도: O(n)
• 상수와는 관계가 없기에 함수를 반복한다거나 하면 이론적으로 이게 O(2N)이 되어야 하지만 '2'는 상수이기 때문에 여전히 O(N)으로 표현하게 된다

2차 시간

def print_twice(arr):
for n in arr:
    for x in arr:
        print(x,n)

• Quadratic Time(2차 시간)
• 2차 시간은 Nested Loops(중첩 반복)이 있을 때 발생한다
• 배열의 각 아이템에 대하여 루프를 반복하여 실행한다.
• 따라서. 시간복잡도는 입력의 N^2인 것이다.
  -> 시간복잡도: O(N^2)
• 입력이 10개라면, 완성하는데 100번의 스텝이 필요하다 / 20개는 400번의 스텝
• 2차 시간과 선형 시간복잡도를 보면 후자가 더 효율적인것으로 선호된다.

3차 시간

def print_third(arr):
for n in arr:
    for x in arr:
    	for y in arr:
	        print(x,n,y)

• 반복문이 3개가 있는 3차시간
• 배열의 사이즈가 10이면 10 x 10 x 10 만큼 루프를 반복한다
  -> 시간복잡도: O(N^3)
• 예시: 삼중 for문, 편상관계 계산, 큐빅

로그 시간

• 로그 시간(Logarithmic time)
• 이진 검색 알고리즘 설명할 때 쓰인다
• 이진 검색 에서는 입력 데이터가 두 배가 되어도 스탭은 딱 1번 밖에 증가하지 않았다
• 왜냐하면 이진 탐색에서는 각 프로세스의 스텝을 절반으로 나눠서 진행
• 이걸 표현하면 O(log N)이 된다
• 로그는 지수의 정 반대다.
• 그렇기에 입력이 두 배가 되어도 검색을 위한 스텝은 +1만 증가한다
• 따라서 이진검색의 시간복잡도는 O(log N)이 된다.
• 선형시간 보단 빠르지만 상수시간보단 느리다
• 단, 이진검색은 정렬되지 않은 배열엔 사용할 수 없다

지수 시간

• 최악의 시간 복잡도로 꼽히는 시간복잡도 이다
• 어떤 상수 c를 n 제곱한 만큼 실행 단계가 커지는 알고리즘
• 여기서 상수 c가 얼마나 큰지는 중요하지 않다. 문제는 지수인 n이다.
• 예시: 피보나치 수열

시간 순서

추가 고려사항

• 내가 짠 메서드나 함수의 시간복잡도를 구할 때 만약 내부에서 또 다른 메서드나 함수를 호출하고 있다면
• 그 메서드나 함수의 시간복잡도를 같이 반영해서 최종적인 시간복잡도를 계산해야 한다.