[Information Theory] 엔트로피에 대해

hmin·2024년 3월 27일

information-theory 엔트로피 정보이론

Information Theory

목록 보기

1/4

Recap

우선 엔트로피를 알기 위해서 Probability와 Random Variable의 내용을 Recap하고 가자.

Probability

probability는 sample space에서 실수 [0, 1]로 매핑해주는 함수 라 볼 수 있다. 따라서 probability function P는 다음 두 공리를 항상 만족해야 한다.

P(S) = 1
Mutually disjoint events A1, A2,…에 대해서 다음 등식이 성립한다.

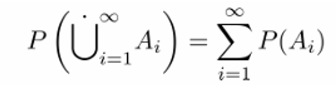
참고로 Mutually disjoint events란 상호베타적인 사건들을 말하며, 동시에 일어날 수 없는 사건들이다.

Random Variables

random variable X는 sample space에서 실수로 매핑해주는 함수 이다.

Ensemble X (X의 앙상블)

ensemble X는 r.v.에 대해 집합을 정의해 놓은 것이다.

$X = (x, A_x, P_x)$
- x : outcome, 가능한 r.v. 집합 중 하나의 집합을 나타낸다.
- A : Alphabet, r.v. x가 가질 수 있는 가능한 값들의 집합
- P : Probability distribution, x에 대한 확률값
Joint Ensemble

XY는 r.v. x와 y의 순서쌍이라 볼 수 있다. 예를 들어 x={x1, x2}, y = {y1, y2}라면 xy={x1y1, x1y2, x2y1, x2y2}이다.
$XY =\{ (x, y), A_X \times A_Y, P_{XY} \}$
joint distribution이 있으면 Marginal probability를 구할 수 있다.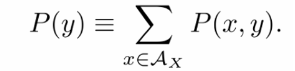

또, 비슷한 맥락으로 Conditional probability 를 구할 수 있다.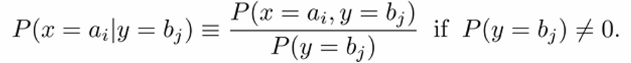

여기까지 random variable과 probability에 대해 잠깐 recap했다. 그럼 이를 바탕으로 이번에는 엔트로피가 무엇이며 어떻게 계산하는지 알아보자.

Entropy

Shannon Information Content

Shannon의 information content는 random variable이 주어졌을 때 얼마만큼의 Uncertainty, 혹은 "Surprise"가 있는지를 수치화한 것이다. 즉, 확률이 높은 "흔한" 데이터가 들어오면 information content 값은 낮다. 반대로 "흔하지 않은" 데이터가 들어오면 값이 높다. 이는 그만큼 놀라운 정보를 의미하여, 이를 bits로 저장해야 할 값들이 많다는 의미이기도 하다. r.v. X가 주어졌을 때 outcome x 의 Shannon information content 는 다음과 같다.

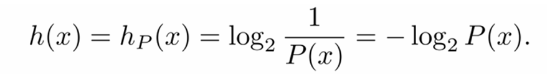
수식을 뜯어보면 x의 확률값이 작을 수록 h(x)값은 커지고, 확률값이 클 수록 h(x)값이 작아지는 형식이다. 따라서 x가 rare한 내용일 수록 정보량이 많다고 보는 것! 이때 log의 밑이 2인 이유는 h(x)의 단위가 bits이기 때문이다.

Entropy

그렇다면 엔트로피는 뭘까? 엔트로피는 쉽게 말하면 Shannon information content의 평균 값이다. 즉, random variable에 대해 평균적으로 담고 있는 정보량을 뜻한다.

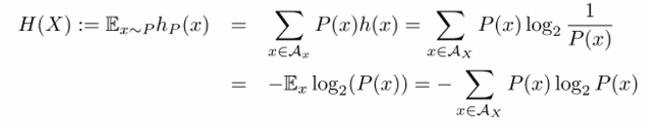
이때 로그의 밑이 2라는 점을 잊지 말자. 보통 생략해서 쓰기 때문!

Shannon의 information contents와 같이 엔트로피도 bits 단위이며, H(X)를 H(p)로 대신해서 사용하기도 한다. 이때 p는 x에 대한 확률 분포이다.

그럼 엔트로피의 프로퍼티를 알아보자.

$H(X) \geq 0$

H(X)는 모든 x에 대해서 0보다 크거나 같다. 왜냐, 수식을 보면 -probability * log(1/probability)인데, 확률은 [0, 1]의 값을 가지기 때문에 무조건 양수 값이 나온다. X가 [0, 0, 1, 0]처럼 one hot vector 꼴로 되어 있다면, 즉 하나의 x에서만 확률이 1이고 나머지는 0인 경우에만 H(X)=0 등식이 성립한다.
p 가 uniform 일 때 엔트로피가 maximize된다.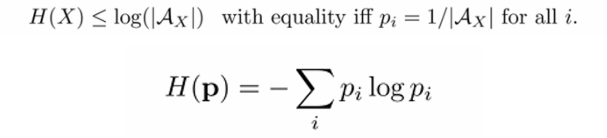

확률 p가 uniform하다는 것은 모든 r.v. x가 동일한 확률 값을 가진다는 것을 의미한다. 그럼 생각을 해보자…. uniform distribution이라면 모든 x에 대해서 p(x) = 1/|A|가 된다.

이때 |A|는 알파 집합의 원소 개수이다. 그럼 모든 i에 대해서 -plog(p)의 합은 결국 -log(p) = log(|A|)와가 되므로 엔트로피의 최댓값이 된다.

Decomposability of the entropy

엔트로피를 활용해보자. 우선 첫 번째로 엔트로피는 분해가 가능하다.

p = \{ p_1, p_2,...,p_I \}

확률 분포가 위와 같이 정의되어있다고 하자. 그럼 이에 대한 엔트로피는

H(p) = -\Sigma_{i=0} ^I \ p_i \log(p_i)

로 정의되어 있다. 여기서 엔트로피는 약간의 트릭을 사용하면 두 개, 세 개 이상으로 분해될 수 있다. 위 엔트로피를 두 개로 분해해보자.

H(p) = H(p_1, 1-p_1) +(1-p_1)H({p_2 \over1-p_1}, ..., {p_I \over 1-p_1} )

증명은 생각보다 간단하다. $p_2 = {1\over 1-p_1}(1-p_1)p_2$ 인 원리를 그대로 적용한 것이다.

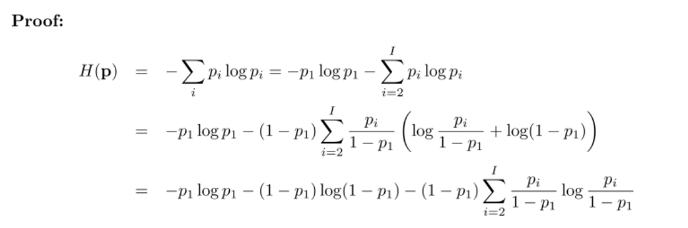
증명을 보면 알겠지만 꼭 $p_1$ 과 나머지로 이등분하는 것만 존재하는건 아니다. 임의의 한 점 m에 대해서 아래와 같이 이등분 하는 것도 가능하다.

이등분만 되는 것도 아니다. 그 이상으로 나누고 싶은 만큼 나누는 것으로 확장할 수 있다.

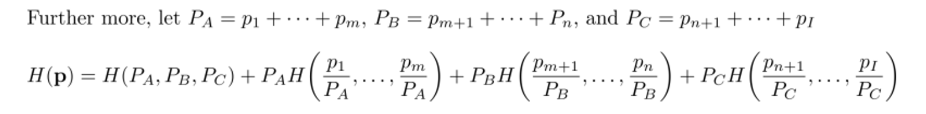
위 예시는 $P_A, P_B, P_C$ 로 총 세 가지로 나눈 것이다.

이렇게 random variable과 probability를 이용하여 엔트로피를 계산할 수 있음을 배웠다. 하지만 여기까지는 하나의 random variable에 대해 하나의 distribution에서의 엔트로피 값을 계산한 것이다. 다음 포스팅에서는 하나의 random variable에 대해 서로 다른 분포들의 엔트로피를 계산해보도록 하자.

hmin

하루 하루 여행

다음 포스트

[Information Theory] 엔트로피에 대해