2. Math Basics

1. 행렬과 벡터

다차원의 정보들을 다룰 때 사용하는 수학적 도구.
행렬의 요소 a 는 일반적인 실수.

1.1. 행렬 (Matrix)

행렬 용어

• 정사각행렬: Square Matrix

• 단위 행렬: Identity Matrix

  $\begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix}$

행렬 연산

• 행렬 합, 차

• 행렬 곱

  $(𝑙×𝑚)⋅(𝑚×𝑛)=(𝑙×𝑛)$

• 행렬 전치 (Transpose)

  $\begin{pmatrix}a & b & c \\ d & e & f\end{pmatrix}^T = \begin{pmatrix}a & d \\ b & e \\ c& f\end{pmatrix}$

행렬 성질

• 교환법칙 X, 결합법칙 O, 분배법칙 O

• 단위행렬 성질

  $MI = IM = M$

  • 항상 Square Matrix

  • 곱셈에서 1(항등원) 역할

  • 단위행렬에 대한 곱셈은 교환법칙 성립

• 전치행렬 성질

  $(AB)^T = B^TA^T$

• 역행렬 (Inverse) 성질

  $AB = I$ 이면 $B = A^{-1}$

  $(AB)^{-1} = B^{-1}A^{-1}$
  
  

1.2. 벡터 (Vector)

벡터는 여러 값을 갖는 다차원의 수를 표현하는 방법이며, 행렬로 표현할 때 행 또는 열의 크기가 1인 특별한 행렬이라고 생각할 수 있음.

열벡터와 행벡터

• 열벡터 (Column Vector)

  $\begin{pmatrix}a \\ b \\ c \end{pmatrix}$

• 행벡터 (Row Vector)

  $\begin{pmatrix}a & b & c \end{pmatrix}$
  
  

열벡터, 행벡터 변환

라이브러리마다 벡터의 표현법이 다름. DirectX, Direct3D 는 행벡터를 사용하며, OpenGL 라이브러리는 열벡터를 사용함. 벡터에 어떤 변환을 위해 행렬을 곱하면, 열 벡터의 경우 벡터의 앞에 행렬을 곱하고, 행 벡터의 경우 벡터의 뒤에 전치된 행렬을 곱함. 벡터는 열벡터를 기본으로 다룰 것임.

• 열 벡터 변환

  $Mv = \begin{pmatrix}a & b \\ c & d \\ e & f \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} ax+by \\ cx + dy \\ ex + fy \end{pmatrix}$

• 행 벡터 변환

  $v^TM^T = \begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix}a & c & e \\ b & d & f \end{pmatrix} = \begin{pmatrix} ax+by & cx + dy & ex + fy \end{pmatrix}$
  $(\ \because (Mv)^T = v^TM^T)$

벡터의 길이

벡터 $v$ = $(v_x, v_y, v_z)$ 의 길이 $\lVert v \rVert$

벡터 정규화 (Normalization)

벡터의 길이 1로 만드는 작업. 벡터를 벡터의 길이로 나눠줌.
정규화 결과 크기가 1인 단위 벡터(Unit vector)를 얻을 수 있음.

2. 기저와 좌표계

기저 (Basis)

• 벡터 공간에서 모든 벡터를 선형 결합으로 표현할 수 있는 벡터들의 집합.
• 즉, 임의의 크기와 방향을 가진 벡터는 Basis vector 의 Linear combination($ax+by$) 로 표현할 수 있음.
• 축이 되는 벡터들.
• 어떠한 베이시스가 주어지든 곱해지는 실수 값만 잘 조절하면 어떠한 벡터든 표현할 수 있음.

좌표계 (Coordinate System)

• 좌표계(Coordinate system)는 원점(Origin) + 기저(Basis) 로 구성됨.
• 컴퓨터그래픽스에서는 공간(Space)과 같은 의미.
• 다양한 기저가 존재하지만 서로 직교하며 크기가 1인 Basis vector 를 사용함.
• 직교하는 것을 Orthogonal 이라고 하며, 직교하면서 크키가 1이면 Orthonormal 하다고 함.

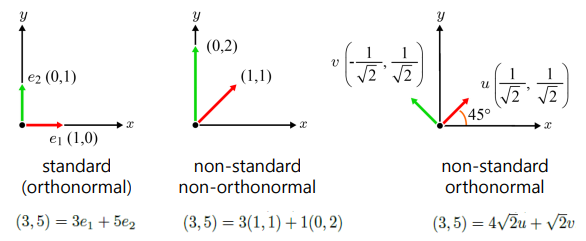
• 일반적으로 사용하는 Standard orthonormal basis (1,0,0), (0,1,0), (0,0,1) 을 사용할 것임.

3. 내적과 외적

내적 (Dot Product, Inner Product)

내적은 구체적인 결과값보다는 두 벡터 간 기하적인 각도 관계를 알기 위해 사용함.

• 대수적 표현

  $\vec{a} \cdot \vec{b} = a_x b_x + a_y b_y + a_z b_z$

• 기하적 표현

  $\vec{a} \cdot \vec{b} = \|\vec{a}\| \|\vec{b}\| \cos\theta$

  수직이면 0, 예각이면 양수, 둔각이면 음수
  
  

외적 (Cross Product)

3차원 공간에서만 정의됨, 오른손 법칙 적용

• 대수적 표현

  $\vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix} = \left(a_y b_z - a_z b_y,\ - (a_x b_z - a_z b_x),\ a_x b_y - a_y b_x \right)$

  $\vec{a} \times \vec{b}$ 는 두 벡터와 모두 수직인 벡터 (오른손 법칙 방향)

• 기하적 표현

  $\|\vec{a} \times \vec{b}\| = \|\vec{a}\| \|\vec{b}\| \sin\theta$

  평행하면(같으면) 0, 평행사변형의 넓이

4. 직선의 방정식과 선형 보간

직선(Infinite Line, Ray)은 그래픽스에서 매개 변수 방정식으로 표현한다. 두 점 $p_0$, $p_1$ 이 있을 때,

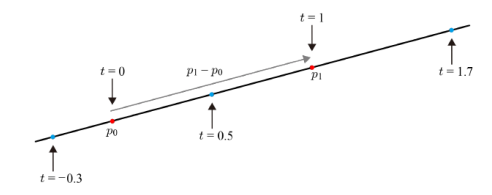
• 한 점 $p_0$ 와 방향 벡터 $p_1 - p_0$ 에 스칼라 $t$ 를 곱함으로써, 직선 위의 한 점에 위치하게 된다.
• 따라서 $t$ 가 0 과 1 사이에 있을 땐 선분(Line Segment) 위에, 그 외에는 직선 위에 위치한다.
• $p_0$ 에서 시작하고 $p_1$ 으로 향하는 점의 운동방정식으로 볼 수도 있다. $t$ 가 양수면 정방향으로 가고, $t$ 가 음수면 역방향으로 가고.

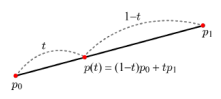
• 식을 전개하면 위와 같이 표현되는데, 선분 위에서 $(1-t)$ 와 $t$ 의 합은 1이다. 이 계수를 가중치인 Weight 라고 부르며, 이 계수의 합이 1이면서 위와 같이 선형 조합을 하게 되면 가중치를 이용해 합을 계산했다고 해서 Weighted Sum 이라고 부른다.
• 이 경우, 두 점을 선형 보간 (Linear Interpolate) 했다고 한다.
• 보간은 이미 알고 있는 데이터 포인트들 사이에 존재하는 값을 추정하는 방법이다.

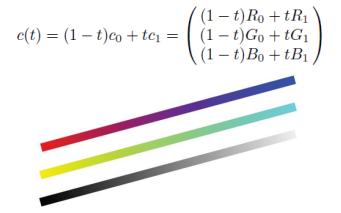
선형 보간을 활용하는 예로 RGB 가 있다. 어떤 RGB 값을 Weighted Sum 형식으로 표현하면, 보간으로 $t$ 에 의해 R 에서 중간색, G 에서 중간색, B 에서 중간색을 결정할 수 있다.

• 작성 일자: 2025-03-30(일)
• 소스 목록:
  • HUFS 25-1학기 컴퓨터그래픽스 2차시
  • [KUOCW] 한정현 컴퓨터그래픽스 (2장-수학 기초)
  • OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문