Binary Indexed Tree (BIT, Fenwick Tree)

지상현·2025년 4월 5일

Binary Indexed Tree(BIT) 는 Prefix sum, Prefix min, Prefix max 등의 값이 자주 변하며 질의(Query) 형태로 이용될 때 질의의 응답 시간을 줄이기 위한 전처리용 자료구조로 사용된다. Fenwick 이 최초로 제안한 것은 아니지만 1994년 그의 논문에서 소개된 이후 Fenwick Tree 라고도 불린다.

기존 Prefix 연산의 수행 시간

Prefix 는 앞에서부터 일정 길이까지 자른 부분이다. n개의 요소를 가진 배열 A가 있을 때, prefix_sum(x) 은 0번째 인덱스부터 x번째 인덱스까지의 합인 A[0] + A[1] + ... + A[x] 이다. 이를 모든 인덱스에 대해 구해서 배열 A와 같은 크기인 배열 P에 저장하기 위한 수행 시간은 O(n) 이다. 왜냐하면 P(x) = A(x) + P(x-1) 과 같이 재귀적으로 구할 수 있기 때문이다.

P를 구해놓으면 A의 구간 합 sum(i, j) 를 상수 시간 O(1) 내에 처리할 수 있다. 예를 들어 A의 3번째 인덱스부터 7번째 인덱스까지의 합을 구하고자 할 때, 일일이 구하면 A[3] + A[4] + ... + A[7] 이 된다. 하지만 P 를 이용하면 P[7] - P[2] 단 한 번의 연산으로 구할 수 있다.

그런데 만약 배열 A의 요소들이 자주 변경된다면? 가령 A[5] += 2 를 수행한다고 하자. A의 요소 값 하나를 변경했는데 P의 경우 계산에 A[5] 가 포함됐던 요소들을 전부 변경해야한다. 즉, P[5] 부터 P[n-1] 까지 모두 += 2 처리해줘야 하기 때문에 P를 업데이트하기 위해 O(n)의 수행 시간이 걸린다.

결론부터 말하자면 BIT 는 초기화에 O(n), 구간 합 sum(i, j) 를 O(logn), 업데이트 update(k, x) 를 O(logn) 에 처리할 수 있다. 즉, 구간 합을 구할 때는 Prefix sum 만을 사용할 때보다 느리지만, 업데이트가 자주 일어나는 경우 Prefix sum 만을 사용할 때보다 빠르다.

	자료구조 초기화	sum(i,j)	update(k, x)
Prefix sum	O(n)	O(1)	O(n)
BIT + Prefix sum	O(n)	O(logn)	O(logn)

Prefix 만큼 자주 쓰이는 것이 Suffix 이다.
Suffix 는 뒤에서부터 일정 길이까지 자른 부분이다.

BIT 의 원리와 사용 이유

Binary Indexed Tree 는 이름 그대로 인덱스를 Binary 로 표현하고 Binary 의 정보를 이용해서 Prefix 를 구할때 활용한다. Tree 라고 하지만 Heap 과 같이 실제로는 배열에 저장되고 트리 모양으로 해석된다.

BIT 는 인덱스가 0이 아닌 1부터 시작한다고 가정한다. 즉, 0번째 원소값은 사용하지 않는다. n개의 값을 가진 배열 A도 A[1] ~ A[n] 까지 사용하고, BIT 배열 T도 T[1] ~ T[n] 까지 사용한다. 실제로 사용할 때 이렇게 하는 편이 훨씬 자연스럽기 때문이다.

BIT 의 아이디어는 prefix_sum(x) 를 작은 합들로 나눠서 구하자는 것이다. x 를 이진수로 표현했을 때 1의 개수만큼 합을 나눠서 표현한다. 예를 들어, prefix_sum(45) 의 경우 45 는 이진수로 101101 이고, 1이 4개이므로 4개의 작은 합으로 표현한다. 각 1이 1, 4, 8, 32 이므로 1개의 합, 4개의 합, 8개의 합, 32개의 합의 작은 합들로 45개의 합을 구할 수 있다. 즉 풀어쓰면 A[45] + (A[44] + ... + A[41]) + (A[40] + ... + A[33]) + (A[32] + ... +A[1]) 이다.

이를 위해 배열 A 요소들의 작은 합들을 미리 구해놓은 게 배열 T 고, 이게 바로 BIT 이다. T[k] 를 구하는 방법은 k를 이진수로 표현했을 때 LSB 값 크기만큼 A 의 요소들을 인덱스 k에서 시작해 인덱스를 감소시키며 더해서 구한다. 여기서 LSB 는 단순히 우측 첫 번째 자리가 아니라, 첫 번째 1의 비트 위치를 의미한다. 예를 들어 T[10] = T[1010(2)] 이고, LSB 가 2이므로 인덱스 10부터 시작해서 2개를 더해서 구한다. 즉, T[10] = A[10] + A[9] 이다. 이를 일반항으로 표현하면 T[k] = A[k] + ... + A[k - LSB(k) + 1] 이다.

왜 이런 방식으로 T 를 구하는 걸까? T 를 이용해 Prefix Sum 을 구해보면 알 수 있다. 앞서 살펴봤던 prefix_sum(45) 를 구해보자. P[45] 는 4개의 작은 합들로 구성된다. 1개의 합, 4개의 합, 8개의 합, 32개의 합. 이는 45를 이진수로 표현하면 101101 이었기 때문이다. 먼저 1개의 합을 찾아보자. T[k] 가 1개의 합이 되려면 LSB 가 1이어야 한다. 바로 T[45] 가 T[101101]로 A[45] 1개의 합이다. 그 다음 4개의 합을 찾아보자. T[44] 가 T[101100] 으로 LSB 가 4이고, A[44] + A[43] + A[42] + A[41] 의 4개의 합이다. 8개의 합은 T[40] 이 T[101000] 으로 LSB 가 8이고, A[40] + A[39] + ... + A[33] 8개의 합이다. T[32] 는 T[100000] 으로 32개의 합이다.

즉, P[k] 는 LSB 를 하나씩 없애면서 T[k] 라는 작은 합들로 나눠서 계산하기 위해 T[k] 를 LSB 의 크기만큼의 작은 합으로 만들어야 하는 것이다. 45 = 1 + 4 + 8 + 32 이고 각각 T[45] + T[44] + T[40] + T[32] 로 P[45] 를 구할 수 있다.

그래서 prefix_sum 을 작은 합들로 나누는 이유가 뭘까? 앞서 Prefix sum 을 살펴봤을 때는 배열 A 의 요소가 하나 바뀌었을 때 최악의 경우 P 의 모든 요소 n 개를 전부 바꿔줘야했다. 하지만 BIT 를 활용하는 경우 인덱스의 이진수 표현의 1의 개수만큼 작은 합들로 나눠서 계산했기 때문에 n의 모든 자리가 1인 최악의 경우에도 $log_2n$ 만큼만 계산하면 된다. 즉, 업데이트의 수행 시간이 O(logn) 이 된다는 장점이 있다.

BIT 를 이용한 Prefix sum, Update, Sum

1. BIT 초기화

T[k] = A[k] + ... + A[k - LSB(k) + 1] 이다. LSB(k) 를 구하는 방법은 다음과 같다.

def LSB(k):
	return k & -k

-k 는 k 의 2의 보수이다. k 와 -k를 비트 연산 & 하게 되면 LSB 만이 살아남는다.

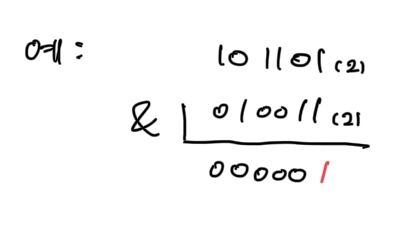
왜냐하면 -k 는 k 를 비트 반전시킨 후 1을 더한 것이기 때문에, LSB 만 같은 숫자가 되어 & 연산 시 LSB 만 살아남는다.

이렇게 T[k] 를 n 개 일일이 구한다면 수행 시간은 O(n) 보다 나쁘다. T[k] 를 구하는 과정도 구간 합이기 때문에 빠르게 초기화하려면 Prefix sum 을 이용한다. 이를 통해 O(n) 시간에 초기화할 수 있다.

2. BIT 를 이용해 Prefix sum 구하기

prefix_sum(k) 는 인덱스 k 의 이진수 표현의 1의 개수만큼 작은 합으로 나눠 더하기 때문에, k 가 $00..00_{(2)}$ 이 될 때까지 매 루프마다 T[k] 를 더하고 LSB(k) 를 빼준다.

def prefix_sum(k):
	s = 0
    while k >= 1:
    	s += T[k]
        k = k - LSB(k)
    return s

수행 시간은 O(logn) 이다.

3. BIT 를 이용해 Update 구하기

update(k, x) 는 배열 A 의 k 번째 인덱스의 값을 x 로 바꾸는 것이다. 그러면 A[k] 를 포함하는 T[k] 들을 어떻게 찾아서 업데이트할까? 기본적으로 T[k] = A[k] + ... + A[k - LSB(k) + 1] 의 정의에 따라 T[k] 는 A[k] 를 포함한다.

여기서 그 다음 T[k] 에도 A[k] 가 계속 포함되려면 T[k] 구간을 포함하는 더 큰 구간을 찾아야 한다. T[k] 는 LSB(k) 의 값의 길이만큼의 합이다. 그 다음 구간은 LSB(k) 를 더해야 캐리가 발생하여 더 큰 구간으로 이동할 수 있다. 따라서 T[k + LSB(k)] 를 통해 T(k) 를 포함하는 그 다음 구간을 찾는다.

def update(k, x):
	d = x - A[k]
    while k <= n:
    	T[k] += d
        k = k + LSB(k)

A[1] 을 업데이트 해도, n의 이진수 자리 갯수만큼 시행되기 때문에 최악의 경우에도 수행 시간은 O(logn) 이다.

4. BIT + Prefix sum 을 이용한 Sum

Sum(i, j) 는 i 와 j 사이의 구간 합을 구하는 함수이다. P[j] - P[i] 를 통해 상수 시간에 수행된다. 이 때, P[j] 와 P[i] 는 BIT 로 구할 때 각각 O(logn) 이 걸리므로, Sum(i, j) 의 수행 시간은 O(logn) 이다.

BIT 를 활용한 순열 복원 문제

문제

1 부터 n 까지 중복 없는 순열을 담은 배열 A 가 있다.

순열은 어떤 집합의 모든 원소들을 특정한 순서로 배열한 것이다.

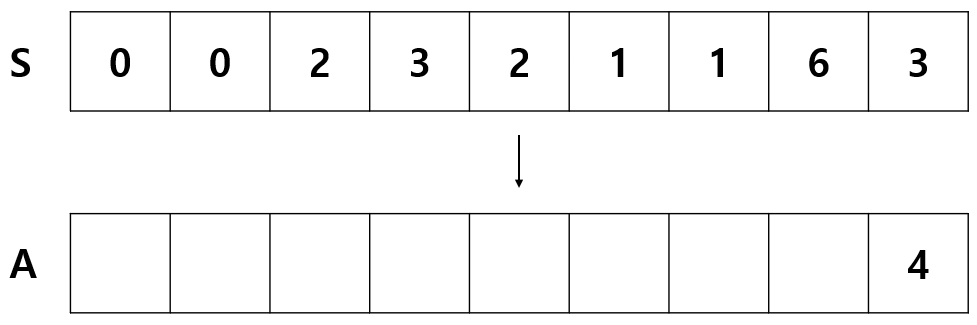
배열 S 는 A 의 각 인덱스 기준 좌측에서 자신보다 작은 수의 개수를 저장한다.

예를 들어 A 의 마지막 인덱스의 값은 4 이기 때문에 자신보다 좌측의 작은 수는 3 개 뿐이다.
따라서 S 의 마지막 인덱스에는 3이 저장된다. 8은 좌측에 자신보다 작은 수가 6개 뿐이므로 S 에 6을 저장한다.

이 때 배열 A 가 유실되었다. 배열 S 를 보고 A 를 복구하려면?

해결법 1번: 우측 인덱스 선형 스캔

S 의 마지막 인덱스부터 본다. 마지막 인덱스의 앞에는 자신을 제외한 모든 수들이 있기 때문에, 자신보다 작은 수가 3개라면 자신은 4임을 알 수 있다.

그 다음은 좌측에 자신보다 작은 수가 6개나 있으니 자신은 최소한 7인데, 우측의 4도 자신보다 작으니 랭크가 하나 올라 8임을 알 수 있다.

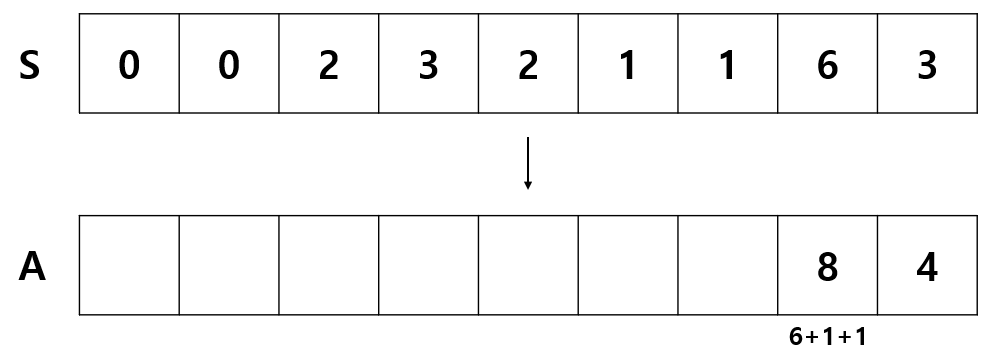
이런 방식으로 전부 찾으면 매 인덱스마다 배열 S 의 인덱스를 찾고, 배열 A 에서 우측 인덱스들을 순회해야하므로,

1 + 2 + ... + n = \frac{n(n+1)}{2} = O(n^2)

수행 시간은 $O(n^2)$ 이다.

해결법 2번: 이진 탐색 + BIT 활용

배열 R 을 하나 두고, 모두 0 으로 초기화한다. 편의상 인덱스는 1부터 시작한다.

배열 R 은 찾은 숫자는 1 로 표시하는 배열이다.
예를 들어 S 를 통해 배열 A 에 4 라는 값을 복구하면 R 의 인덱스 4가 1이 된다.

해결법 1번 방식과 마찬가지로 S 의 마지막 인덱스부터 살펴본다.
마지막 인덱스 값의 랭크는 3 + 1 = 4 이다. (A의 우측은 스캔하지 않는다.)
배열 R 의 비어있는 칸 중 4번째 칸에 들어가야 한다.

이진 탐색을 위해 반으로 쪼개 좌측을 선택한다.

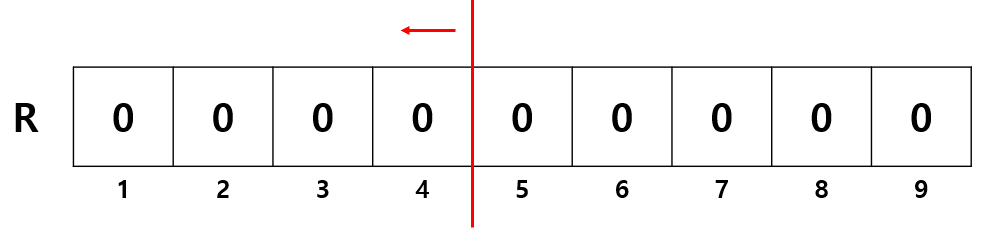
1부터 4까지의 구간에서 빈 칸의 개수를 구해야 한다.
찾은 칸은 1이 저장되기 때문에 구간의 크기 - sum(i,j) 를 통해 구할 수 있다.
왜냐하면 sum(1,4) 는 1부터 4까지의 구간의 찾은 칸의 개수이기 때문이다.
sum(i,j) 의 경우 배열 R 의 BIT 를 활용해 2개의 prefix_sum 으로 처리할 수 있다.

구간의 크기(4) - sum(1,4)(0) 이므로 총 4칸이 비어있고 랭크 ≤ 빈 칸의 개수 이면 현재 구간에 값이 들어갈 수 있다는 뜻이다. 따라서 랭크(4) ≤ 빈 칸의 개수(4) 이므로 좌측이 선택되었다.

다시 반으로 쪼개 좌측을 선택한다.

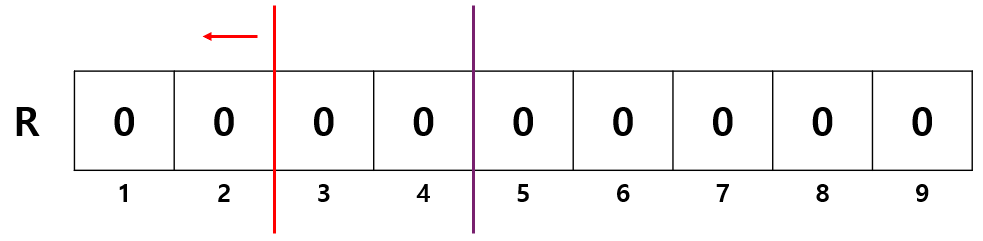
빈 칸의 개수는 구간의 크기(2) - sum(1,2)(0) 이므로 총 2칸이 비어있고 랭크(4) > 빈 칸의 개수(2) 이므로 들어갈 수 없다. 따라서 우측을 선택한다. 우측을 선택할 때는 랭크를 좌측의 빈 칸의 개수를 빼서 갱신한다. 따라서 랭크를 4 - 2 = 2 로 갱신한다.

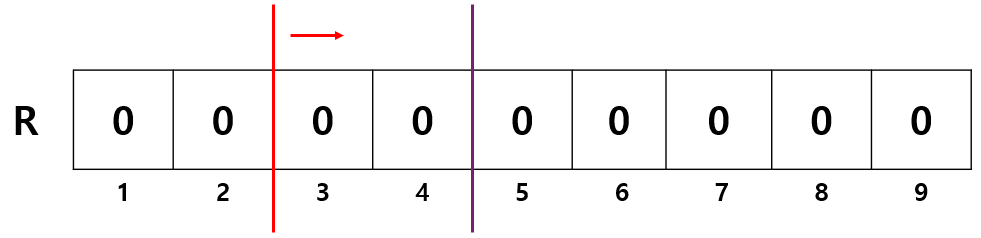
우측을 보니 구간의 크기(2) - sum(3,4)(0) 으로 2칸 비어있고, 랭크(2) ≤ 빈 칸의 개수(2) 이므로 들어갈 수 있다. 따라서 우측이 선택되었다.

다시 반으로 쪼개 좌측을 선택하는데, 1칸 비어있고 랭크(2) > 빈 칸의 개수(1) 이므로 우측을 선택한다. 우측을 선택함에 따라 랭크를 2 - 1 = 1 로 갱신한다. 우측은 1칸 비어있고 랭크(1) ≤ 빈 칸의 개수(1) 임에 따라 선택된다.

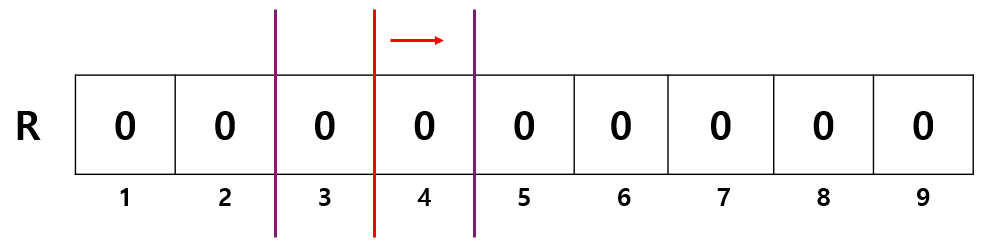
마지막으로 반으로 쪼개면, low > high 라는 종료 조건을 만나 종료한다.
배열 R 의 BIT 를 통해 4번째 인덱스에 1 값을 갱신하고, 배열 A 에 값을 복원한다.
이를 모든 인덱스에 대해 반복해서 배열 A 를 복원할 수 있다.

요약하자면,

배열 R 은 A의 찾은 값을 1로 표시하는 배열이다.
R 을 이용해 마지막 인덱스부터 역순으로 A 의 값들을 복원한다.
이진 탐색을 통해 좌측부터 선택하고, 빈 칸의 개수를 구간의 크기 - sum(i,j) 로 센다.
빈 칸의 개수 ≤ 값의 랭크 면 좌측 구간에 값을 담을 수 있고, 다시 반으로 쪼개며 종료 조건을 만날 때까지 반복한다.

값의 랭크는 배열 S 에서의 값 + 1 이다.
빈 칸의 개수 > 값의 랭크 면 좌측 구간에 값을 담을 수 없고, 우측 구간을 선택한다.
우측 구간을 선택할 때 값의 랭크를 값의 랭크 - 빈 칸의 개수 로 갱신한다.
다시 반으로 쪼개며 종료 조건을 만날 때까지 반복한다.

이 경우 수행 시간은 $O(nlog^2n)$ 이다.

인덱스 하나를 찾기 위한 이진 탐색: $O(logn)$
이진 탐색 시마다 BIT 를 활용한 sum(i,j) 연산: $O(logn)$
종료 시에 BIT 를 활용한 R 업데이트: $O(logn)$

따라서 1-3번은 $O(log^2n + logn) = O(log^2n)$ 이며,
이를 모든 인덱스에 대해 반복하면 n 번 수행하여 $O(nlog^2n)$ 이 된다.

작성 일자: 2025-04-05(토)

수정 내역

2025-04-09(수) BIT 를 활용한 순열 복원 문제 추가

소스 목록:

HUFS 25-1학기 고급문제해결기법및실습 4차시

고급문제해결기법및실습 강의노트 pp. 95-101

신찬수 교수님 유튜브: 자료구조 이진인덱스트리 (1/2)

신찬수 교수님 유튜브: 자료구조 이진인덱스트리 (2/2)

신찬수 교수님 유튜브: 알고리즘 - 순열복원문제 알고리즘 해설