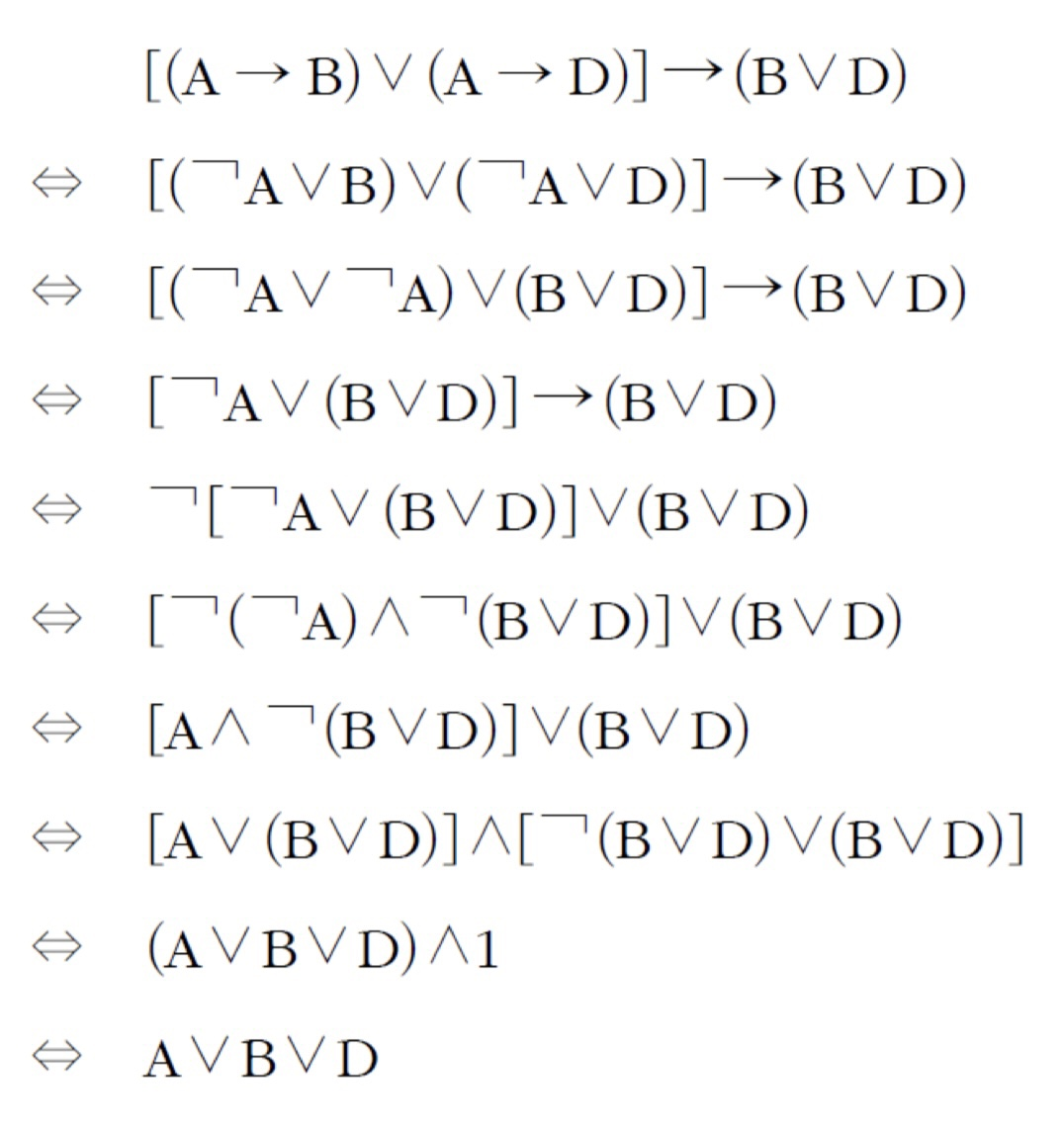공부하는 중이라 부정확하고 부족한 지식일 수있습니다! 댓글로 지적 부탁드립니다!
논리적 추론(Logic inference)
명제
명제(Proposition)
- 참이나 거짓 중 단 하나만 갖는 문장
- 명제 중에서 명제의 내용이 참이 되는 명제를 참 명제(Truth proposition)
- 명제 중에서 명제의 내용이 거짓이 되는 명제를 거짓 명제(False proposition)
진리값
진리값(Truth value)
- 참과 거짓을 명제의 진리값이라 함.
- 참을 T 또는 1, 거짓을 F 또는 0으로 표시함.
예제1
Examples of propositons
- 1 + 0 = 1 -> T (truth value)
- 0 + 0 = 2 -> F (truth value)
논리연산자
- 논리곱(Conjunction, AND, ∧)
- 논리합(Disjunction, OR, ∨)
- 부정(Negation, NOT, ¬)
- 배타적 논리합(Exculsive OR, XOR, ⊕)
- 논리 함축(Implication, →)
- 동치(Equivalence, ↔)
- 전제(Premise)
- 결론(Conclusion)
- 역(Converse)
- 대우(Contraposition)
- 이(Inverse)
진리표
진리표(Truth table)
- 논리 연산자에 대한 논리 연산표
- 참과 거짓을 나타내는 T,F 또는 1,0으로 표에 나타냄.
-
논리곱(Conjunction) 진리표
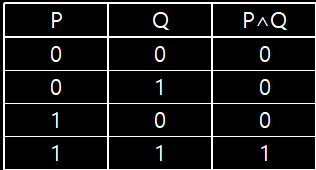P 명제와 Q 명제 중 둘 다 1(참)일 때 논리곱 P∧Q은 1, 나머지 0 -
논리합(Disjunction) 진리표
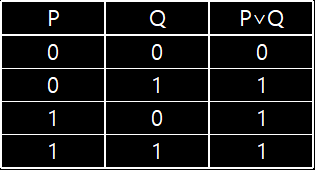P 명제와 Q 명제중 1개 이상이 1(참)이면 논리합 P∨Q는 1, 나머지는 0 -
부정(Nagation) 진리표
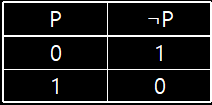주어진 1개의 명제의 1(참)과 0(거짓)을 반전시켜주는 논리연산
P가 1 이면 ¬P는 0
P가 0 이면 ¬P는 1 -
배타적 논리합(Exculsive OR) 진리표
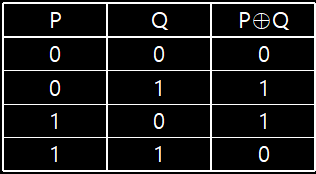주어진 명제 중 1(참)이 홀수 개일때 배타적 논리합 P⊕Q는 1, 나머지는 0 -
논리 함축(Implication) 진리표
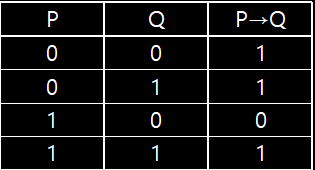P가 1(참)이고 Q가 0(거짓)일 경우에만 0(거짓)이 되고, 그 외에는 모두 1(참)
P→Q 는 ¬P와 Q의 논리합, P→Q = ¬P∨Q -
논리적 동치(Equivalence) 진리표
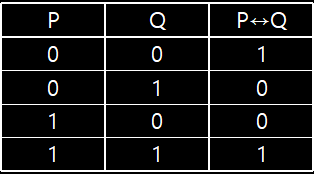P와 Q가 모두 1(참)이거나 모두 0(거짓)일 경우에만 1(참)이 되고 그 외에는 모두 0(거짓)
P↔Q는 P→Q 와 Q→P의 논리곱, (P→Q)∧(Q→P) = P↔Q
예제2
Example of Truth table
- ¬(P∧Q)→(¬P∨Q)의 진리표를 구하여라
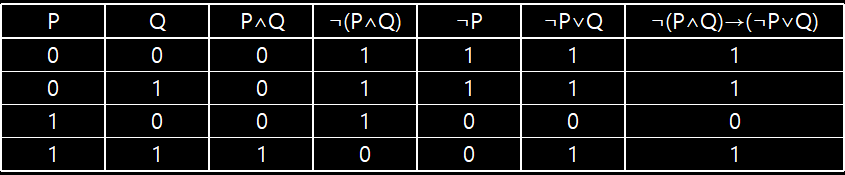
- (P→Q)∧(Q→P)의 진리표를 구하여라
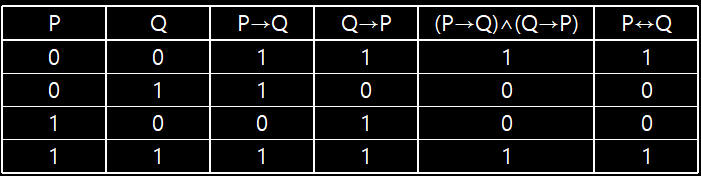진리표를 보면 (P→Q)∧(Q→P)와 P↔Q가 똑같음을 알 수 있다. - ((P∨Q)∧¬R)→P의 진리표를 구하여라
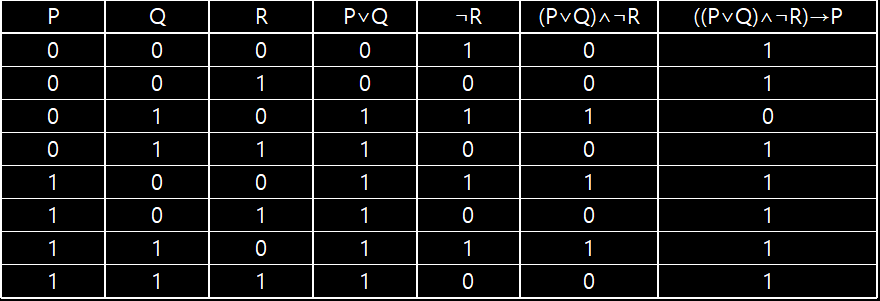
연산자 우선 순위표
연산자 우선 순위표(Operator precedence table)
- 진리표를 작성하기 위해서는 우선순위가 정해져야 함
- 우선순위를 위해 괄호를 사용하기도 하지만, 명제가 길고 복잡하면 괄호 때문에 가독성 🠗
- 가독성을 높이기 위해 연산자 우선순위표 사용
- 연산자들의 우선순위와 결합 법칙을 이용하여 우선순위 결정
연산자들의 우선 순위
- ¬(부정) > ∧(논리곱) > ∨(논리합) > →(논리함축) > ↔(논리적 동치)
- 연산자 우선 순위를 유지하고 ¬(부정)은 "오른쪽 결합법칙"
나머지 연산자들은 "왼쪽 결합법칙"을 가진다고 가정
- P∧Q → ¬P∨Q∧R 를 예시로 보자
- 위 명제에서 사용하는 연산자는 ¬,∧,∨,→
- 표에서 열에 있는 연산자는 스택 속 연산자
- 표에서 행에 있는 연산자는 입력 속 연산자
- 1행 1열을 보면 스택 속에 ¬ 연산자가 있고, 입력 속에도 ¬ 연산자가 있음.
- 같은 연산자이므로 연산자 우선 순위가 같음.
- ¬은 오른쪽 결합 법칙을 가지므로 입력에 ¬ 연산을 먼저 수행
- 2행 2열을 보면 스택 속에 ∧ 연산자가 있고, 입력 속에도 ∧ 연산자가 있다.
- 같은 연산자이므로 연산자 우선 순위가 같음.
- ∧은 왼쪽 결합 법칙을 가지므로 스택에 ∧ 연산을 먼저 수행
- 같은 방법으로 주대각 원소에 있는 우선순위를 채워보면 다음과 같다.
- 1행 2열을 보면 스택 속에 ¬ 연산자와 입력 속에 ∧ 연산자가 있는데 ¬ 연산자가 우선 순위이니 스택을 우선순위로 채울 수 있다.
- 같은 방법으로 나머지 부분도 채워보면 다음과 같다.
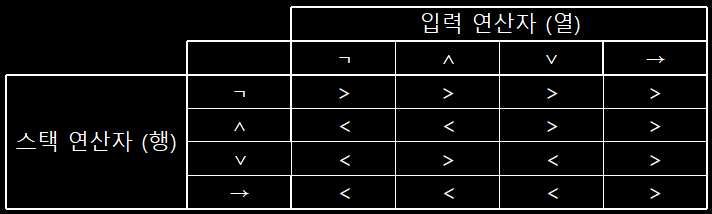
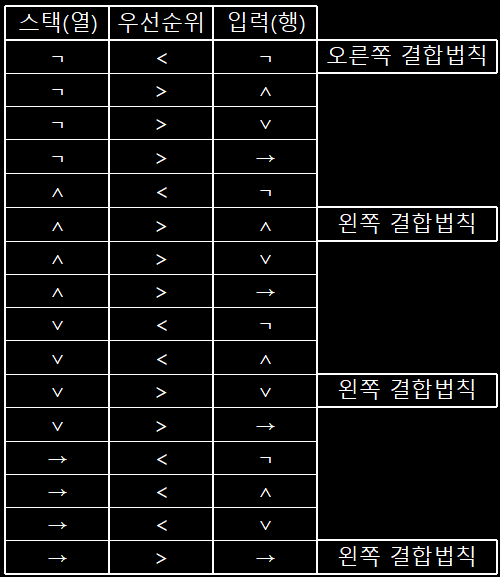
연산자 우선 순위표를 이용한 연산
- 위 표를 이용해 P∧Q → ¬P∨Q∧R에 대해서 계산해보자.
- 연산자 스택(¬,∧,∨,→), 피연산자 스택(P,Q,R)을 사용
- 입력은 왼쪽에서 오른쪽으로 하나씩 읽음.
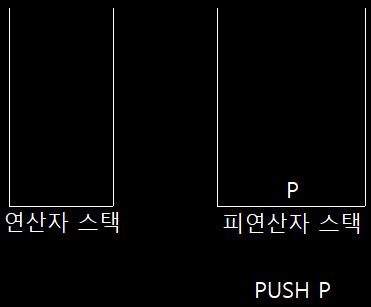
- 1단계
피연산자 P 스택에 넣음 => PUSH P 실행
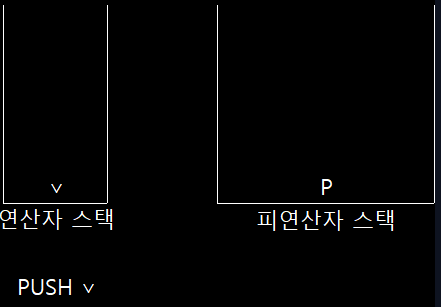
- 2단계
연산자 ∧ 스택에 넣음 => PUSH ∧ 실행
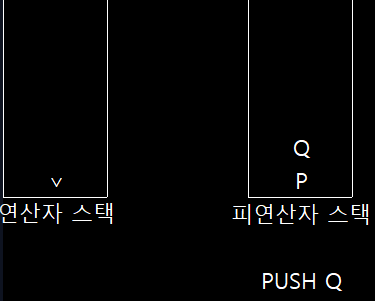
- 3단계
피연산자 Q 스택에 넣음 => PUSH Q 실행
- 4단계
연산자 스택이 우선순위 높음 => 연산
- 5단계
연산자 → 스택에 넣음 => PUSH → 실행
- 6단계
입력 연산자가 우선순위 높음 => PUSH ¬ 실행
- 7단계
피연산자 P 스택에 넣음 => PUSH P 실행
- 8단계
연산자 스택이 우선순위 높음 => 연산
- 9단계
입력 연산자가 우선순위 높음 => PUSH ∨ 실행
- 10단계
피연산자 Q 스택에 넣음 => PUSH Q 실행
- 11단계
입력 연산자가 우선순위 높음 => PUSH ∧ 실행
- 12단계
피연산자 R 스택에 넣음 => PUSH R 실행 => 입력이 끝남
- 13단계
연산자 스택에 아무것도 없을때까지 반복하여 연산자 스택에서 POP하고 피연산자 스택에서 POP하여 연산하고 연산한 값을 피연산자 스택에 PUSH
- 14단계
13단계 반복
- 15단계
13단계 반복
- 연산 순위
1순위 : (P∧Q) 논리 곱 연산
2순위 : (¬P) 부정 연산
3순위 : (Q∧R) 논리 곱 연산
4순위 : ((¬P)∨(Q∧R)) 논리 합 연산
5순위 : (P∧Q) → ((¬P)∨(Q∧R)) 논리 함축 연산
예제3
Example of Operator precedence table
-
P∨Q∧¬R → P를 연산자 순위표를 이용해서 순위를 매겨라
-
1단계
피연산자 P 스택에 넣음 => PUSH P 실행 -
2단계
연산자 ∨ 스택에 넣음 => PUSH ∨ 실행 -
3단계
피연산자 Q 스택에 넣음 => PUSH Q 실행 -
4단계
입력 연산자가 우선순위 높음 => PUSH ∧ -
5단계
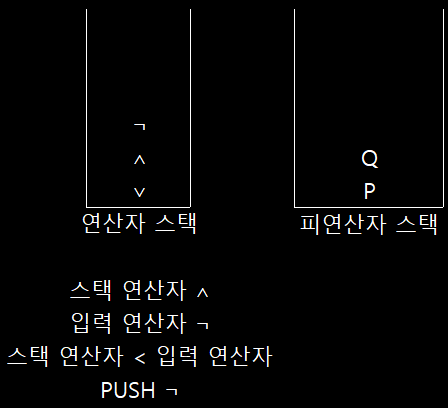입력 연산자가 우선순위 높음 => PUSH ¬ -
6단계
피연산자 R 스택에 넣음 => PUSH R -
7단계
스택 연산자가 우선순위 높음 => 연산 -
8단계
스택 연산자가 우선 순위 높음 => 연산 -
9단계
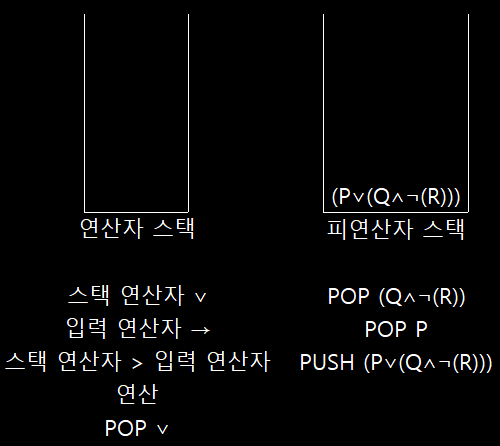스택 연산자가 우선 순위 높음 => 연산 -
10단계
연산자 → 스택에 넣음 => PUSH → 실행 -
11단계
피연산자 P 스택에 넣음 => PUSH P -
12단계
입력 끝 => 연산
P∨Q∧¬R → P
- 연산 순위
1순위 : (¬R) 부정 연산
2순위 : (Q∧(¬R)) 논리 곱 연산
3순위 : (P∨(Q∧(¬R))) 논리 합 연산
4순위 : (P∨(Q∧(¬R))) → (P) 논리 함축 연산
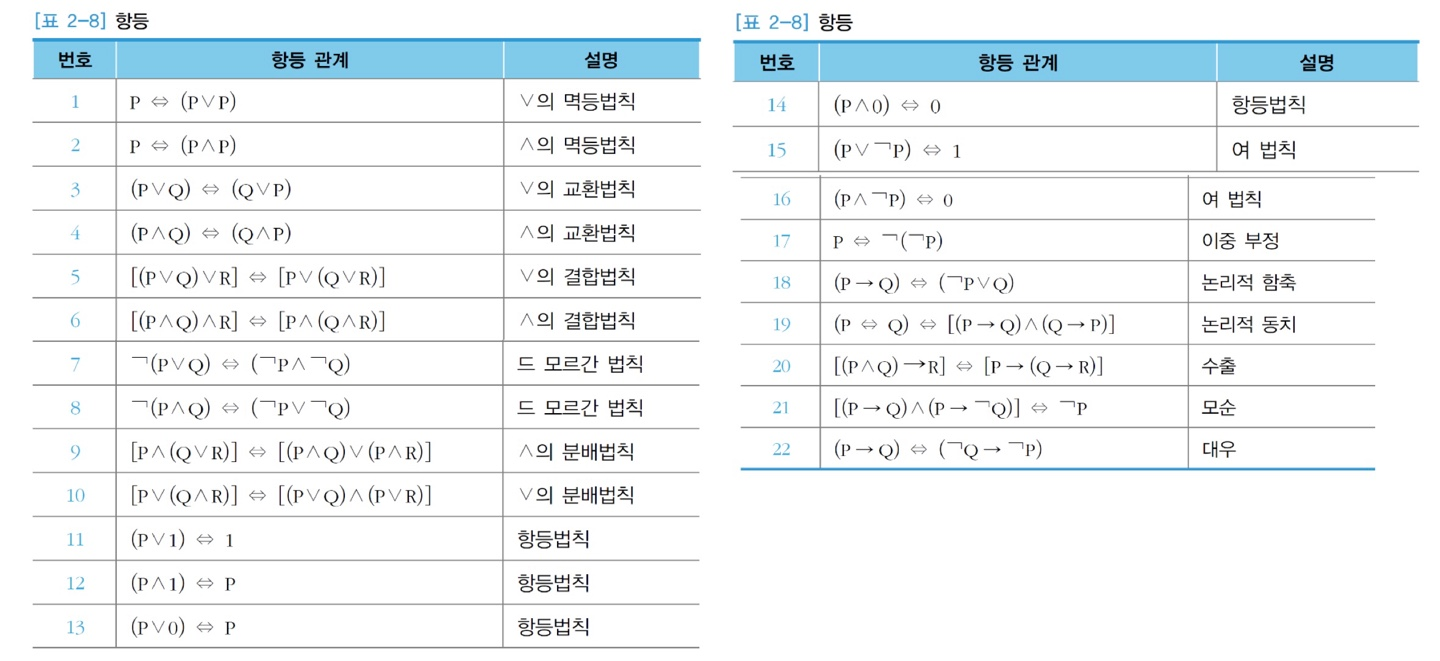
항등
항등(Identity)
논리적 동치(Equivalence)란 P와 Q가 똑같은 진리값을 갖는 것을 말하고 논리적으로 동치인 명제로 명제들을 간단히 할 때 사용
예제4
다음 명제를 항당을 이용하여 간단히 만들어보자.
- [(A→B)∨(A→D)] → (B∨D)
