[알고리즘] Dynamic Programming

우노·2024년 4월 8일

알고리즘

Algorithm

목록 보기

2/10

주어진 복잡한 문제를 여러 개의 작은 문제 (하위 문제, subproblem)으로 나누어서 풀고 그 결과를 저장/결합,
⚡즉 재활용하여 최종 문제를 해결하는 알고리즘

계산 횟수를 줄여 효율적인 계산이 가능하고
특히 제곱 등 하위 문제 수가 기하급수적으로 증가할 때 유용하다.

점화식 형태 의 수식을 풀이하는 알고리즘으로 기억하면 편할 것 같다.

메모이제이션(Memoization)

: 함수 호출의 결과를 캐싱하고 동일한 입력이 다시 발생할 때 불필요하게 다시 계산하는 대신 캐싱된 결과를 반환하는 프로그래밍 기술
메모리라는 공간 비용을 투입해 계산에 소요되는 시간 비용을 줄이는 방식

타뷸레이션(Tabulation)

: 계산 결과를 테이블에 저장하여 큰 문제를 단계적으로 해결하는 방식

위의 두 개념을 참고하면 점화식을 풀이하는 방식은 두가지가 가능하다.

Top-Down vs Bottom-up

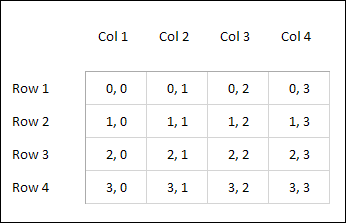예를 들면 위 사진과 같은 배열이 미로라고 가정하자.
오른쪽과 아래로만 이동해서

(0, 0) → (3, 3) 까지 가는 방법
= (0, 0) → (3, 2) + (0, 0) → (2, 3) = … 
= (0, 0) → (1, 0) + (0, 0) → (0, 1) + …

위와 같이 큰 문제를 작은 문제들로 표현할 수 있다.

각 칸을 방문하고 각 칸까지 가는 방법의 수를 계산하는 법이

하나의 재귀 함수 호출
값을 저장해둔 배열의 한 칸

이 될 수 있다.

또 하나의 예로 피보나치 수열을 살펴보자.

F_n = F_{n-1} + F_{n-2} (F_1=F_2=1)

여기서 Fn이 하나의 재귀 함수 호출이나 값을 저장하는 배열 한 칸이 될 수 있다.

Top-Down; 재귀 호출

int Fibonacci(int n) {
	if (n == 1)    return 1;
	if (n == 2)    return 1;
	return Fibonacci(n-1) + Fibonacci(n-2);
}

// main에서 호출
Fibonacci(n);

❌ Subproblem으로 나누어 풀지만 기존 결과를 재활용하지 않는다.
🚨 이 재귀 방식은 함수 호출마다 계산이 이루어지기 때문에 메모이제이션이 아니다!

vector<int> fibo(n+1, 0);
fibo[0] = 0;  fibo[1] = 1;  fibo[2] = 1;

int Fibonacci(int n) {
	if (fibo[n] == 0)
		memo[n] = Fibonacci(n-1) + Fibonacci(n-2);
	return memo[n];
}

⭕ 이렇게 활용해야 메모이제이션이다!

n == 1 | n == 2 까지 쪼개진 다음에 두 경우의 리턴값을 받기 전까지
이전의 함수 호출은 계산이 미뤄지며
N번째 피보나치 숫자라는 큰 문제를 1, 2번째부터 차례로 계산할 수 있다.

⇒ N을 쪼개서 작은 문제로 나누어 계산한다는 점에서 하향식 접근임을 알 수 있다.

Bottom-up; 배열 저장

int Fibonacci(int n) {
	vector<int> fibo(n+1, 0);
	fibo[0] = 0;  fibo[1] = 1;  fibo[2] = 1;
	for(int i=3; i<n+1; i++) {
		fibo[i] = fibo[i-1] + fibo[i-2];
	}
	return fibo[n];
}

🏓 이건 타뷸레이션 방식이다!

이미 알려진 초기값을 배열에 저장해두고 배열의 값을 새로 계산하고 저장하는 과정을 반복한다.
N번째 피보나치 숫자라는 큰 문제를 1, 2번째 값으로부터 나온 값을 차례로 계산하고 저장하며 이를 활용하여 최종 문제를 해결할 수 있다

⇒ N을 작은 문제부터 계산해서 결과값을 도출한다는 점에서 상향식 접근임을 알 수 있다.

메모이제이션 (메모리) vs 타뷸레이션 (테이블)

메모이제이션
👍 직관적, 하향식 접근
👎 함수 호출 메모리 스택, 호출 시간이 오버 헤드

타뷸레이션
👍 효율적, 상향식 접근
👎 생각이 어려울 수도

DFS/BFS에 익숙하다면 위의 두 경우를 비교하는 데에 메모이제이션-DFS / 타뷸레이션-BFS 를 떠올리면 이해가 쉬울 것 같다.
~~물론 DFS-재귀, BFS-자료구조 를 주로 활용한다는 점에서 생각한 비유일 뿐 둘은 저언혀 다른 알고리즘임을 분명히 해야한다 !!!~~

새로운 문제에 직면했을 때