[알고리즘] Sorting

우노·2024년 5월 27일
알고리즘

Algorithm

목록 보기
10/10
post-thumbnail

1️⃣ 교환 정렬

🫧 버블 정렬(Bubble sort)

서로 인접한 두 원소를 비교하는 것을 반복하여 정렬

로직

  1. k번째와 k+1번째 원소를 비교하여 기준에 따라 정렬한다. (1≤k<N)
    → N번째에 가장 큰 원소 배치
  2. 1번의 종료 기준을 k<N 일 때부터 k<1일 때까지 반복한다.
    → k번째에 (N+1)-k번째로 큰 원소 배치

⇒ 오름차순 정렬 완료 

#include <algorithm>

void Bubble_Sort(int arr[], int N) {
  for(int i=N-1; i>0; i--){
	  for(int j=0; j<i; j++){
		  if(arr[j] > arr[j+1])
			  swap(arr[j], arr[j+1]);
	  }
  }
}

시간복잡도:

O(n(n+1)2)=O(n2)O(\frac{n(n+1)}{2}) = O(n^2)

최적화: 한 사이클에서 원소를 비교할 때 swap이 발생하지 않는다면 이미 정렬된 상태이므로 반복문을 종료할 수 있다.

➕ 파생형으로 칵테일 정렬(cocktail sort; 홀수번째를 돌 때는 처음부터, 짝수번째를 돌 때는 마지막부터 확인하는 정렬)과 빗질 정렬(comb sort; 바로 옆 원소가 아닌 k번째 뒤의 원소와 비교하여 정렬), 홀짝 정렬(odd–even sort; 목록 안의 인접한 요소들의 색인화된 홀/짝 쌍을 모두 비교)이 있다.

⏩ 퀵정렬 (Quicksort)

분할 정복(Divide and Conquer)과 다른 원소와의 비교를 활용하는 정렬

로직

  1. 배열에서 하나의 원소를 골라 기준인 pivot으로 부른다.
  2. pivot 앞에는 pivot보다 값이 작은 모든 원소들을, pivot 뒤에는 pivot보다 값이 큰 모든 원소들이 오도록 배열을 둘로 나눈다. ⇒ 분할
  3. 분할된 두 개의 배열에 대해 배열의 크기가 0이나 1이 될 때까지 재귀적으로 반복한다.

⇒ 오름차순 정렬 완료

#include <algorithm>

void QuickSort(int arr[], int left, int right) {
    if(left >= right) return; 

    int i = left;
    int mid = (left+right)/2;
    for(int j=left; j<right; j++){
	    if(arr[j] < arr[mid])
		    swap(arr[i++], arr[j]);
    }
    swap(arr[i], arr[mid]);
    
    QuickSort(arr, left, i-1);
    QuickSort(arr, i+1, right);
}

재귀 호출이 한번 진행될 때마다 최소한 원소 하나(위 코드에서는 arr[mid])의 위치가 결정되므로 알고리즘이 무한히 반복되지 않으며 정렬이 완료될 수 있다.

시간복잡도:

O(n2)O(n^2)

최악 - 피봇을 계속 최대/최소로 선정

O(n  log2n)=O(n  logn)O(n\;log_2n) = O(n\;logn)

최선 - 거의 비슷한 두 부분집합으로 나뉠 때

O(n  logn)O(n\;logn)

평균

기타

유머를 위한 알고리즘이거나 비효율적이라고 여겨지는 버블소트보다 더 비효율적인 알고리즘이다.
종류만 알고 넘어가자.

2️⃣ 선택 정렬

✔️ 선택 정렬(Selection sort)

최솟값 찾기를 반복하는 정렬

로직

  1. 배열 인덱스 0 ~ N-1 까지 비교하여 최솟값을 찾아 배열의 첫 인덱스 위치에 배치한다.
  2. 1.을 첫 인덱스를 k (0≤k≤N-1)로 하여 반복한다.

⇒ 오름차순 정렬 완료

#include <algorithm>

void Selection_Sort(int arr[], int N) {
  for(int i=0; i<N; i++){
	  int min = MAX_INT, idx = 0;
	  for(int j=i; j<N; j++){
		  if(min > arr[j]){
			  min = arr[j];
			  idx = j;
		  }
	  }
	  swap(arr[i], arr[idx]);
  }
}

시간복잡도:

O(n(n+1)2)=O(n2)O(\frac{n(n+1)}{2}) = O(n^2)

힙 정렬(Heap sort)

힙(heap, 우선순위 큐)를 활용하는 정렬

로직

  1. 배열의 모든 값을 최대 힙에 삽입한다.
  2. 최대 힙에서 값을 하나씩 제거하며 최대 힙에 남은 원소 중 최댓값을 찾아 배치한다.

⇒ 오름차순 정렬 완료

#include <algorithm>
#include <queue>

void Heap_Sort(int arr[], int N) {
	priority_queue<int> pq;
	int idx = N;
	for(auto a:arr)
		pq.push(a);
  while(!pq.empty()){
	  int top = pq.top();
	  pq.pop();
	  arr[--idx] = top;
  }
}

시간복잡도:

O(nlogn+n)=O(nlogn)O(nlogn + n) = O(nlogn)

힙에 삽입하여 최대 힙을 재구성하는 O(log n)을 n번 반복한다.

3️⃣삽입 정렬

⤵️ 삽입 정렬(Insertion sort)

배열에서 자신의 위치를 찾아 삽입

로직

  1. 1 ~ k-1번째 까지 이미 정렬된 배열이 존재한다.
  2. k번째 원소를 골라 이미 정렬된 배열에서 자신의 위치를 찾아 삽입한다.
  3. k를 2부터 N까지 반복한다.

⇒ 오름차순 정렬 완료

#include <algorithm>
#include <queue>

void Insertion_Sort(int arr[], int N) {
	for(int i=1; i<N; i++){
		int temp = arr[i], j=i;
		for(int j=i-1; j>=0; j--){
			if(temp < arr[j])
				arr[j+1] = arr[j];
			else
				break;
		}
		data[j+1] = temp;
	}
}

시간복잡도:

O(n(n+1)2)=O(n2)O(\frac{n(n+1)}{2}) = O(n^2)

기타

삽입정렬을 사용하거나 삽입정렬에서 파생된 알고리즘이다.

  • 이진삽입정렬(Binary InsertionSort): 새로운 원소 삽입을 이진 탐색을 활용하여 정렬 O(nlogn)
  • 셸 정렬(Shell's sort) - 삽입 정렬을 띄엄띄엄한 간격으로 먼저 수행하고, 그 간격을 점차 좁혀나가는 방식 O(n^1.25) ~ O(n^2)
  • 라이브러리 정렬(library sort) - 삽입 속도를 빠르게 하기 위해 배열에 간격을 두는 알고리즘 O(n) / O(nlogn) / O(n^2)
  • 트리 정렬(Tree sort) - 이진탐색트리를 만들어 정렬 O(nlogn)

4️⃣ 병합 정렬

➕ 병합 정렬(Merge sort)

분할정복 알고리즘의 일종으로 병합하며 정렬

로직

  1. 배열의 크기가 1 이하이면 정렬 종료
  2. 배열을 더이상 나누어지지 않을 때까지 재귀를 통해 둘로 나눈다.
  3. 나누어진 두 배열의 원소를 비교하여 정렬하며 합친다.

⇒ 오름차순 정렬 완료

// Top-down
// Bottom-up도 가능하지만 Top-down이 보다 직관적
void MergeSort(int A[], int low, int high, int B[]){
    if(low >= high) return;

    int mid = (low + high) / 2;

    mergeSort(A, low, mid, B);
    mergeSort(A, mid+1, high, B);

    int i=low, j=mid+1;
    for(int k=low; k<=high; k++){
        if(j > high ) B[k] = A[i++];
        else if(i > mid) B[k] = A[j++];
        else if(A[i] <= A[j]) B[k] = A[i++];
        else B[k] = A[j++];
    }

    for(i=low; i<=high; i++) 
	    A[i] = B[i];
}

시간복잡도:

O(n  logn)O(n\;logn)

5️⃣ 분배 정렬

기수 정렬(Radix sort)

  • 기수(데이터를 구성하는 기본 요소 ex. 숫자 0~9, 알파벳 a~z)를 활용하여 정렬
  • 데이터의 직접적인 비교가 불필요
  • 데이터는 크기가 유한하고 사전순으로 정렬할 수 있어야 하며 길이가 같거나 다르면 같게 만들어서 정렬해야 함
  • 정렬의 이론상 한계인 O(nlogn)을 뛰어넘을 수 있음
  1. LSD(Least Significant Digit)
    가장 작은 자릿수부터 정렬
    ex. 170, 45, 75, 90, 2 
    - 170, 45, 75, 90, 2  // 170, 045, 075, 090, 002
- 170, 90, 2, 45, 75  // 1의 자리로 정렬
- 2, 45, 170, 75, 90  // 10의 자리로 정렬
- 2, 45, 75, 90, 170  // 100의 자리로 정렬
  2. MSD(Most Significant Digit)
    가장 큰 자릿수부터 정렬
    ex. 170, 45, 75, 90, 2 
    ```
- 170, 45, 75, 90, 2  // 170, 045, 075, 090, 002
- 45, 75, 90, 2, 170  // 100의 자리로 정렬
- 2, 45, 75, 90, 170  // 10의 자리로 정렬
- 2, 45, 75, 90, 170  // 1의 자리로 정렬
```
    시간복잡도:
O(kw)    (k=데이터의  개수,  w=데이터의  길이)O(kw)\;\;(k=데이터의\;개수,\; w=데이터의\;길이)




계수 정렬(Counting sort)

  • 원소가 나타나는 횟수를 누적하여 원소의 위치를 탐색하고 정렬
  • 작은 양의 정수들과 최댓값이 작을 때 유리

ex. 3, 5, 1, 3, 1, 4, 1

  • 횟수 계산
12345
30211
  • 누적 → 인덱스 계산
12345
03356

⇒ 1, 1, 1, 3, 3, 4, 5

시간복잡도:

O(n+k)    (k=데이터의  최댓값)O(n+k)\;\;(k=데이터의\;최댓값)

6️⃣ 하이브리드 정렬

팀 정렬(Tim sort) : 병렬+삽입 / 대부분 이미 정렬되어있는 배열에 유리 O(n) ~ O(nlogn)
블록 병합 정렬(Block merge sort): 병합 정렬 개조 (삽입+병합) / O(n) ~ O(nlogn)
인트로 정렬(Intro sort): 퀵+힙 / C++의 std::sort() 에서 주로 사용 O(nlogn)
스프레드 정렬(Spreadsort): 분배 정렬+비교 정렬의 분할


7️⃣ 기타

➡️ 위상 정렬(Topology sort)

순서가 정해져있는 작업을 순서대로 정렬하기 위한 알고리즘이며 그래프에 사용할 수 있다.

ex. 가능한 순서 케이스는 아래와 같다.

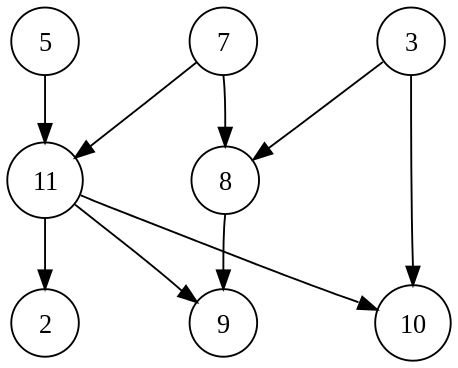
  • 5, 7, 3, 11, 8, 2, 9, 10 ( 맨 위에서 왼쪽에서 오른쪽으로 아래까지 )
  • 3, 5, 7, 8, 11, 2, 9, 10 ( 제일 작은 수부터 이용 가능한 첫 꼭짓점까지 )
  • 5, 7, 3, 8, 11, 10, 9, 2 ( 왼쪽 맨 위를 처음으로 )
  • 7, 5, 11, 3, 10, 8, 9, 2 ( 가장 큰 수부터 이용 가능한 첫 꼭짓점까지 )
  • 7, 5, 11, 2, 3, 8, 9, 10 ( 맨 위부터 왼쪽에서 오른쪽으로 시도하여 아래까지 )
  • 3, 7, 8, 5, 11, 10, 2, 9 ( 제멋대로 )


참고 자료: https://ko.wikipedia.org/wiki

profile
우노
기록하는 감자
이전 포스트

[알고리즘] Divide and Conquer

0개의 댓글