[Algorithm] DFS(깊이 우선 탐색)

2021-07-22

! 약 3주에 걸친 앱잼 기간 동안 계속 앱만 만들다가 이제 일상으로 돌아와 다시 알고리즘 공부를 시작하려고 한다. 저번에 구현에 대해 공부했으므로 이번에 다음 챕터인 DFS/BFS에 대한 공부 내용을 작성해봤다.
<자료 : 이것이 코딩 테스트다 with 파이썬>

1. 스택, 큐

DFS와 BFS는 대표적인 탐색 알고리즘으로 이 둘을 제대로 이해하기 위해서는 기본 자료구조인 스택과 큐에 대한 이해가 전제되어야 하지만 나는 학교 자료구조 시간에 배웠기 때문에 간단하게 작성하고 자세한 내용은 생략할 것이다.

스택은 선입후출(FIFO) 또는 후입선출(LIFO)구조, 큐의 경우는 선입선출(FIFO)구조이다.

파이썬으로 큐를 구현할 경우 collections 모듈에서 제공하는 deque 자료구조를 활용하는 것이 유용하다.

2. DFS(깊이 우선 탐색)

그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘.

• DFS는 스택 자료구조를 이용해 구체적인 동작 과정은 다음과 같다.

1. 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.

2. 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문 처리를 한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.

3. 2번의 과정을 더 이상 수행할 수 없을 때까지 반복한다.

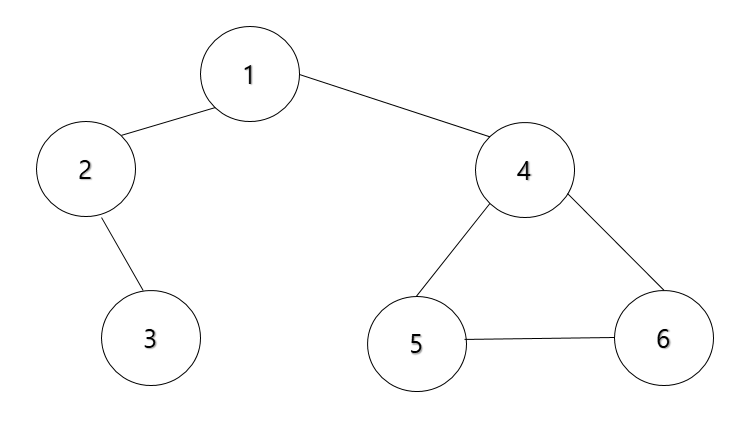
그림을 통해 과정을 보자면,

1. 시작 노드인 '1'을 스택에 삽입한 후에 방문 처리를 한다.

2. 스택의 최상단 노드('1')에 방문하지 않은 인접 노드들 중 작은 노드인 '2'를 스택에 넣고 방문 처리를 한다.

3. 스택의 최상단 노드('2')에 방문하지 않은 인접 노드들 중 작은 노드인 '3'을 스택에 넣고 방문 처리를 한다.

4. 최상단 노드('3')에 방문하지 않은 인접한 노드가 없으므로 스택에서 '3'을 꺼낸다.

5. 마찬가지로 '2'도 스택에서 꺼낸다.

6. 다음 스택의 최상단 노드('1')에 방문하지 않은 인접한 노드 '4'를 슽택에 넣고 방문 처리를 한다.

7. 방문하지 않은 노드가 없을 때까지 계속해서 방문

순서 : 1 - 2 - 3 - 4 - 5 - 6

DFS는 스택을 이용하는 알고리즘으로 실제 구현에 있어서는 재귀 함수를 이용했을 때 간결하게 구현이 가능하다.

3. 예제 코드

def dfs(graph, v, visited):
	visited[v] = True  #방문처리
    print(v, end=' ')
    
    for i in graph[v]:
    	if not visited[i]:
        	dfs(graph, i, visited)
            
graph = [
	[],
    [2,4],
    [1,3],
    [2],
    [1,5,6],
    [4,6],
    [4,5]
    ]    		#2차원 리스트로 표현
    
visited = [False] * 9

dfs(graph, 1, visited)	#DFS 함수 호출

DFS / BFS 문제를 풀어보면서 느낀건데 둘 사이를 정확하게 구분하기가 어려웠다.

그래서 찾아본 결과 DFS의 경우는 모든 노드를 방문해야할 때, 미로 탐색 시에 이동할 때마다 가중치가 붙는 경우, 이동과정에 제약이 있을 경우 사용한다.