! 이진 탐색을 공부하면서 앞서 배웠던 퀵정렬과 비슷한 방식이라고 생각되어서 생각보다 쉽게 이해가 되었다. 역시 공부하면 된다
1. 순차 탐색
이진 탐색에 대한 공부전에 순차 탐색에 대해 이해할 필요가 있다.
순차 탐색은 리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 차례대로 확인하는 방법이다.
보통의 경우 정렬되지 않은 데이터를 찾아야 할 때 사용하며 시간이 충분할 경우 항상 원하는 데이터를 찾을 수 있다.
우리가 리스트 자료형에서 특정한 값을 가지는 원소의 개수를 세는 count() 메소드를 이용할 때도 내부에서 순차 탐색이 수행된다.
2. 이진 탐색
배열 내부의 데이터가 정렬되어 있어야만 사용 가능하고 탐색 범위를 절반씩 좁혀가며 데이터를 탐색한다.
위치를 나타내는 변수 3개를 사용하는데 탐색하고자 하는 범위의 시작점, 끝점, 중간점이다.
찾으려는 데이터와 중간점 위치에 있는 데이터를 바복적으로 비교하여 원하는 데이터를 찾는 것이 이진 탐색의 과정이다.
그림을 통해서 자세하게 알아보도록 하자.
- 1단계
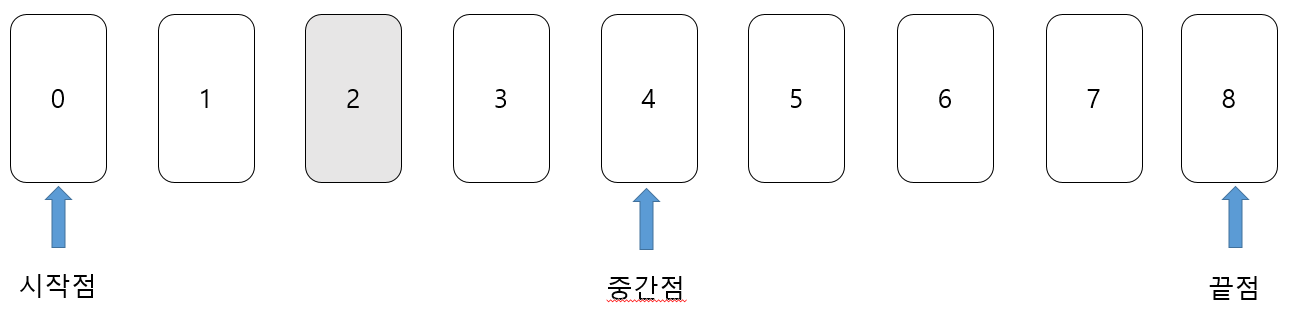
우리는 회색으로 칠해진 '2'라는 데이터를 찾고자 한다.
먼저, 중간점을 설정하는데 중간점이 실수일 경우에는 소수점 이하를 버린다. 다음 그림에서는 시작점의 인덱스가 '0', 끝점의 인덱스가 '9'이므로 중간점의 인덱스는 4.5에서 소수점을 버린 '4'가 된다.
다음으로 중간점의 데이터인 '4'와 찾으려는 데이터 '2'를 비교한다. 중간점의 데이터인 '4'가 더 크기 때문에 끝점을 중간점 '4' 이전인 '3'으로 옮긴다.
- 2단계
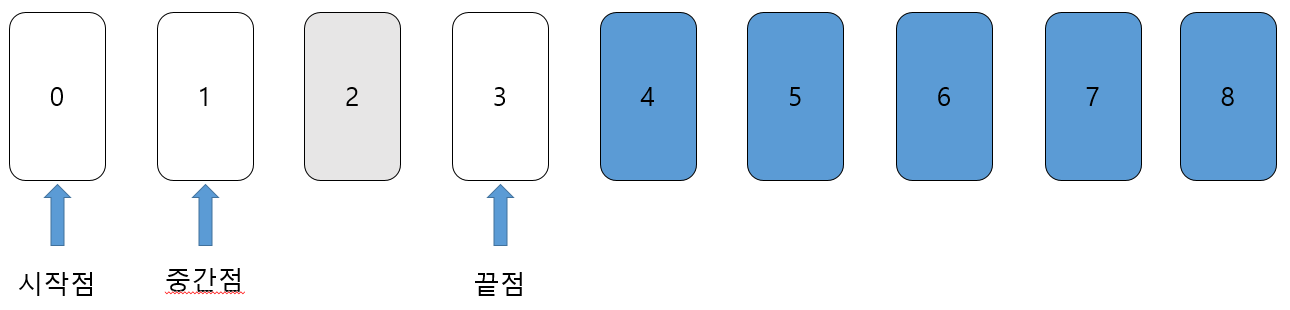
시작점은 그대로 '0'이고 끝점은 '3'. 중간점은 1.5에서 소수점을 버린 '1'이다. 중간점인 '1'이 찾으려는 데이터 '2'보다 작기 때문에 값이 '2' 이하인 데이터는 더 이상 확인할 필요가 없다. 그러므로 시작점을 '2'로 변경한다.
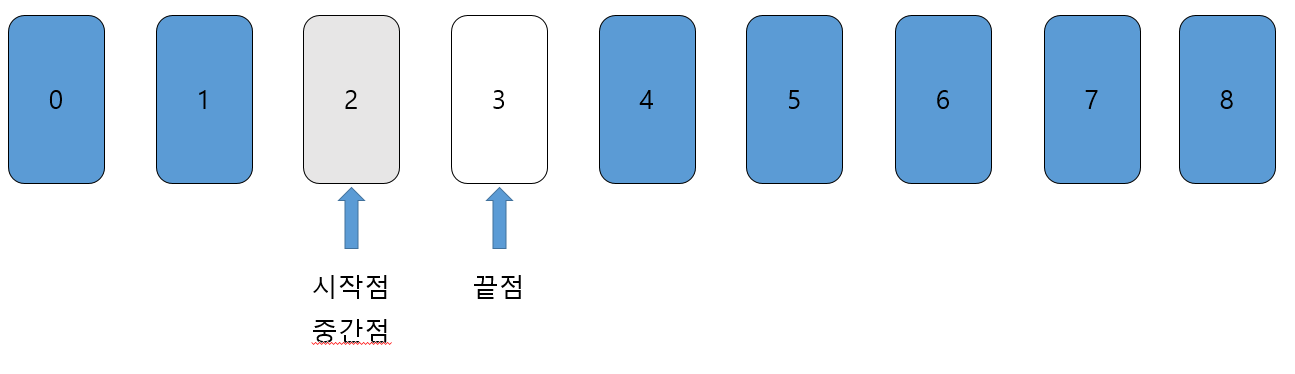
- 3단계
시작점은 '2'이고, 끝점은 '3'이다. 이때 중간점은 2.5에서 소수점을 버려 '2'이다. 중간점에 있는 데이터는 우리가 찾으려는 데이터 '2'와 같기 때문에 탐색을 종료하고 return한다.
그림을 통해 알아봤듯 이진 탐색의 경우 확인을 진행할 때마다 확인하는 원소의 개수가 절반씩 줄어들기 때문에 시간 복잡도가 O(logN)이다. 이와 같은 시간 복잡도는 우리가 정렬에서 배웠던 퀵 정렬과 같다.
이진 탐색의 경우에는 재귀함수와 반복문을 이용하여 구현할 수 있다.
- 코드 구현(재귀 함수)
def binary_search(array, target, start, end):
if start > end:
return None
mid = (start + end) // 2
if array[mid] == target:
return mid
elif array[mid] > target:
return binary_search(array, target, mid + 1, end)
else:
return binary_search(array, target, mid + 1, end)
n, target = list(map(int, input().split())
array = list(map(int, input().split()))
result = binary_search(array, target, 0, n-1)
if result == None:
print("원소가 존재하지 않는다.")
else:
print(result + 1)
- 코드 구현(반복문)
def binary_search(array, target, start, end):
while start <= end:
mid = (start +end)//2
if array[mid] == target:
return mid
elif array[mid] > target:
end = mid - 1
else:
start = mid + 1
return None
# 다음은 재귀함수와 동일Tip) 이진 탐색 문제는 탐색 범위가 큰 상황에서의 탐색을 가정하는 경우가 많다. 따라서 탐색 범위가 2,000만을 넘어갈 경우 이진 탐색으로 문제를 접근해보는 것이 좋다. 1,000만을 넘어갈 경우에도 O(logN)의 시간복잡도를 가진 알고리즘을 떠올려 보는 것이 유용하다!

