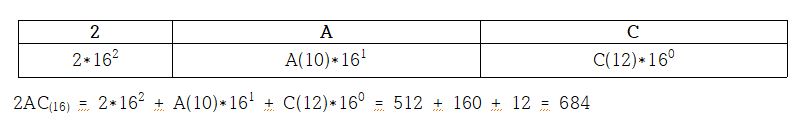Ch02. 변수

ho_c·2023년 3월 23일
CS자바의 정석 3판
0

자바의 정석 3판

목록 보기
1/8
post-thumbnail
post-custom-banner

들어가는 말

  • 프로그래밍 언어의 기본은 자료, 곧 Data를 다루는 일이다.
    물론 반복문, 제어문으로 흐름 제어도 있지만, 자료가 없으면 컴퓨터가 딱히 할 일은 없을 것이다. 그래서 컴퓨터에게 일을 시키기 위한 첫 번째 단계는 값을 던져주는 일이고, 컴퓨터에게 값을 던져주는 공간을 “변수”라고 한다.

1. 변수와 상수


변수란?

  • 단 하나의 값을 저장할 수 있는 메모리 상의 공간.

  • 쉽게 말해 변수란 아파트 우편함과 유사하다. 또는 헬스장 락커처럼 물건을 넣을 수 있는 공간이라고 이해하는게 편하다. 그리고 이 공간은 운영체제에 의해 관리된다.

￮ 요약

  • 메모리상의 공간

  • 하나의 변수에 하나의 값만 저장 가능

  • 변수의 선언과 초기화

  • 변수를 사용하기 위해선 1) 선언 2) 초기화의 과정을 거친다.


변수 선언

  • 공간을 사용하기 위해선 분류가 필요하듯이 변수를 사용하기 위해선 해당 변수의 용도와 이름을 컴퓨터에게 알려줘야 한다.
int age;

int는 변수타입, age는 변수명인데 실제 변수명은 메모리 상에서 “주소”의 형태로 관리된다.
사람이 이해하기 편하게 변수명으로 대체되는 것이다.
이제 우리는 변수명이란 주소를 이용해 메모리에 접근해 변수를 다룰 수 있게 된다.


초기화

  • 초기화는 선언된 변수에 처음으로 값을 넣어주는 것이다.
    단순한 초기화는 변수 선언과 함께 진행해 따로 절차를 구분하진 않는다.
    그래도 초기화를 왜 해야되는지는 알아야 한다.

  • 메모리는 CPU의 작업 대상을 미리 올려놓는 휘발성 저장공간이다.
    그래서 단순 작업 중에도 보이지 않는 프로그램들이 메모리 상에 올라가 운용되고, 이를 운영체제에 의해 스케쥴링 되고 있다.

그래서 우리가 선언한 변수 안에 미쳐 치우지 못한 데이터들이 있을 수도 있어서, 대입연산자(=)를 통해 해당 값을 변수 안에 저장시켜 초기화 한다.

int age;
age = 25;

￮ 요약

  • 변수를 쓸려면 컴퓨터한테 알려줘서 메모리를 특정해 한다.
  • 메모리는 공간을 주소 형태로 운용, 즉 변수는 실제 형태는 ‘주소’이다.
  • 이걸 인간이 직접 하나씩 외우기엔 불편하다.
  • 고로 변수명을 사용, 또한 변수타입으로 공간의 용도를 특정해줘야 한다.
  • 초기화를 안하면 이전 값이 남아있을 때도 있다.

두 변수의 값 교환하기

int x = 20;
int y = 10;

두 변수가 있다. 이 둘의 값을 바꿔보자.

방법은 간단하다.
만약 양손에 사과가 있다고 치자, 이 둘의 위치를 바꾸려면 어떻게 해야될까?
저글링을 하면 쉽겠지만, 컴퓨터는 저글링을 못한다.

단, 한번에 바꿀려 하지말고 한 손의 사과를 바닥에 내려놓고 옮긴 다음 내려놓은 사과를 남은 손으로 잡으면 된다.

위 방식대로 하면 그냥 변수 하나 더 선언하면 된다.

int x = 20; // 왼손
int y = 10; // 오른손
int tmp; // 바닥

tmp = x; // 바닥에 내려놓고
x = y; // 오른손에 있는 걸 왼손으로 옮기고
y = tmp; // 바닥에 있는 걸 오른손으로 집어든다.

변수의 명명규칙

  • 맘대로 지을 수 있다면 좋겠지만, 그러면 혼란이 온다.
    또 프로그래밍 언어마다 미리 특정된 언어(예약어)들이 존재하기 때문에 이는 피해야 한다.
    따라서 구분을 위한(식별) 규칙이 있다.

 ① 대소문자 구분, 길이 제한 X
 ② 예약어는 변수명으로 사용하면 안된다.
 ③ 숫자로 시작하면 안된다.
 ④ 특수문자로 ‘_’와 ‘$’만 허용된다.

예약어는 쓰다 보면 외워진다. 미리 외워봤자 그 용도를 모르기 때문에 딱히 달달 외워둘 필요는 없다.

추가로 프로그래머 간의 convention은 중요하다. 일종의 예의이니 미리 숙지해두는게 좋다.

  • 클래스 명의 첫 글자는 대문자
  • 여러 단어로 이루어진 이름은 카멜 케이스로 구분 (IndexOf)
  • 상수는 모두 대문자, 이때 여러 단어는 스네이크 케이스로 구분 (MAX_NUMBER)

2. 변수의 타입

  • 컴퓨터로 다루는 값은 모두 ‘숫자’지만, 인간의 관점에선 ‘문자와 숫자’ / 숫자는 ‘정수, 실수’로 구분된다.

  • 그리고 이것들이 다 표현하는 범위가 다르고, 메모리를 다루는 방식이 다르기에 값의 종류를 미리 나누어 놨는데, 이를 “자료형”이라고 한다.


기본형과 참조형

  • 자료형은 기본형과 참조형으로 나뉜다.
    이 둘은 메모리 상에서 다루는 위치가 구분된다. 자세한 건 나중에 보도록 하자.

  • 무튼 기본형에는 실제 값 자체가 들어가고, 참조형에는 실제 값이 저장되어 있는 “주소”를 값으로 가진다.

굳이 예를 들면 지하철 물건 보관함에 기본형은 돈가방이, 참조형엔 돈가방의 위치가 들어있다고 생각하면 된다.

기본형 예

int a = 10;

참조형 예

Date today = new date();

  • 참조변수는 클래스 타입을 변수 타입으로 가져가며, 앞서 말한 것처럼 객체의 주소를 저장한다. - 여기서 new연산자는 클래스를 인스턴스화 하는 예약어이다.
    이제 today이라는 참조변수명을 통해서 Date 인스턴스를 사용할 수 있다.

  • 이때 참조변수의 주소는 null or 0x0~0xFFFFFFFF로 저장된다. (JVM 32bit)
    16진수 한자리 = 4bit


￮ 요약

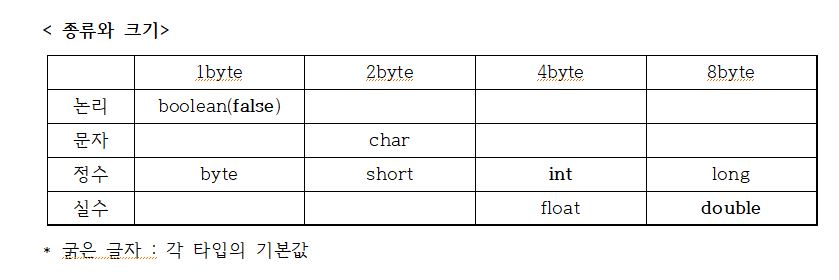
  • 기본형 : boolean(논리), char(문자형, 사실상 정수), { byte, short, int, long }(정수), { float, double }(실수)
  • 참조형 : 객체 주소
  • 참조변수는 클래스 타입을 변수 타입으로 가져감
  • C언어와 달리 참조형 변수와는 연산 불가다.

기본형

  • 기본형은 8개(boolean, char, byte, short, int, long, float, double)이 있으며,
    논리, 정수, 실수으로 구분한다.
    (char도 실방식은 정수, 그래서 정수형과 연산이 가능하다.)

이러한 구분은 저장방식과 저장할 값의 범위의 영향을 받았다.

￮ 요약

  • 기본형(8개)은 저장방식, 크기, 범위에 따라 논리, 정수, 실수로 구분된다.
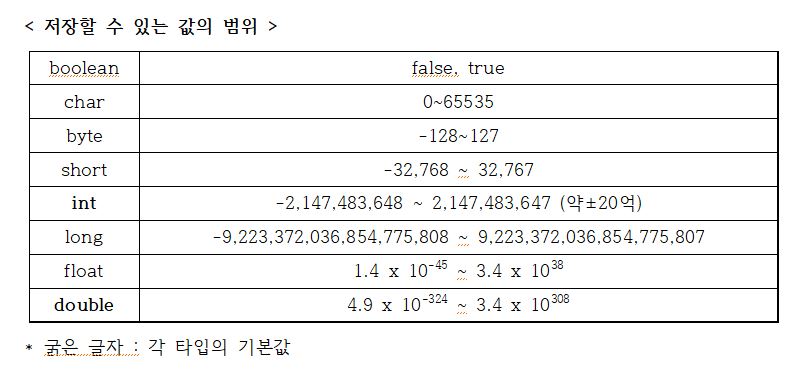
  • 정수의 범위(2n−12^{n-1}~2n−12^{n-1}−1-1) 대충 int는 10자리, long은 19자리이다.
  • 실수는 정밀도가 중요하다. float(7) : 소수점 6자리까지 / double(15) : 소수점 14자리까지

상수와 리터럴

1) 상수(constant)

  • 상수(constant) 역시 값을 저장할 수 있는 메모리 공간이다.
    다만 한번 저장하면 다른 값으로 변경할 수 없다.

선언 방법은 변수와 동일하지만, 상수 앞에는 final이라는 예약어가 붙는다.

final int MAX_Value = 10; // int타입 상수 선언과 초기화

￮ 요약

  • 상수는 선언과 초기화가 동시에 해야만 한다.
  • 대문자 표기가 관습이며, 스네이크 케이스(_)로 단어를 구분한다.

2) 리터럴(literal)

  • 실제 저장되는 값들 역시 상수이다.
    다만 기존 상수의 정의와 구별하기 위해 값은 ‘리터럴’이라고 칭한다.

3) 상수의 필요성

  • 상수는 코드의 유지보수성을 높이기 위해서 사용된다.
final int WIDTH = 20;
final int HEIGHT = 10;

int triangleArea = (WIDTH * HEIGHT) / 2;

위 코드에서 삼각형의 면적을 변경하고 싶으면 상수만 변경하면 된다. 물론 변수여도 가능하지만 상수는 중간에 값을 변경할 수 없기 때문에 코드의 안정성 면에서 적합하다.


4) 리터럴의 타입과 접미사

  • 리터럴 역시 타입이 존재한다. 변수 타입이 있으니, 그에 맞는 값의 타입 역시 존재하는게 맞다.

￮ 요약

  • 값 자체의 타입을 구별하기 위해서 리터럴의 타입이 존재한다.
  • 자세한 건 표를 참조
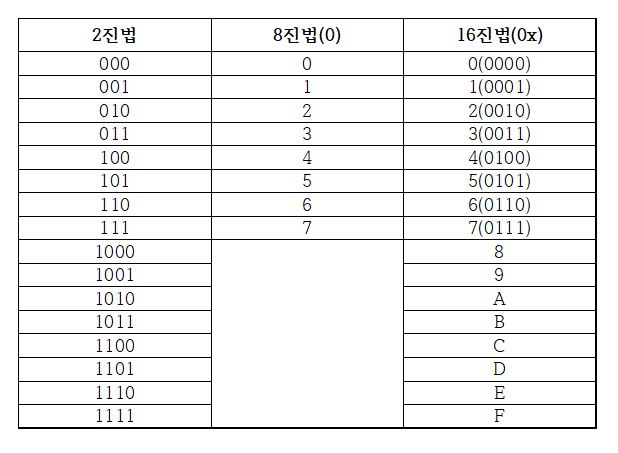
  • 진법 표현도 가능 { 2진법 : 0b / 8진법 : 0 / 16진법 0x }
  • 리터럴이 큰 경우 _로 단위를 구분할 수 있다.
  • 타입이 존재하기 때문에 작은 타입의 변수에 큰 타입의 리터럴을 넣으면 컴파일 에러가 발생한다.

5) String 문자열

  • “”로 감싸면 문자열로 자동으로 인식한다.
    하지만 String은 응용 메서드가 포함된 클래스이다. 이때 다음 두 코드는 내부적으로 차이가 있다.
 String name = new String("Java");
 String name = "Java";

형식화된 출력 printf()

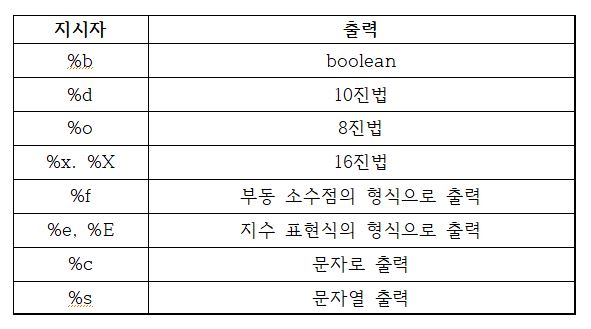
  • printf()는 지시자를 사용하여 변수의 값을 여러 가지 형식으로 변환해서 출력할 수 있다.
    이때 지시자는 값을 어떻게 출력할 것인지 지정해주는 역할을 한다.

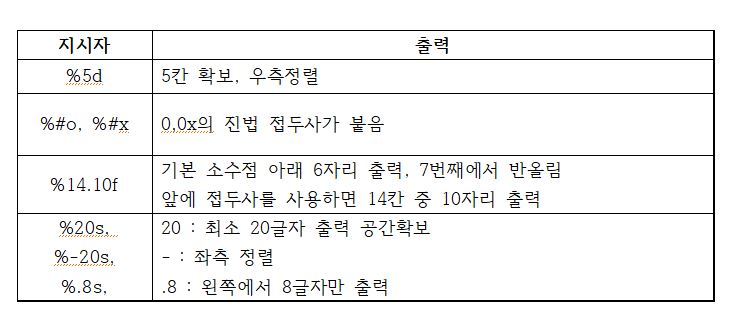
지시자 응용

  • 지시자와 함께 접두사를 사용하여 응용할 수 있다. 다음 예시를 보자.

화면에서 입력받기 Scanner

  • Scanner 클래스는 사용자로부터 동적으로 데이터를 입력 받는 기능이 있다.
Scanner scanner = new Scanner(System.in);
String input = scanner.nextLine();

  • 객체 생성 후, nexLine() 메서드로 변수의 값을 저장할 수 있다. 이 메서드는 다음 순서로 동작한다.
     ① 메서드 호출
     ② 입력 대기 상태 -> 입력 완료(Enter)
     ③ 입력값을 문자열로 반환

  • 추가적인 메서드들을 통해서 값의 타입을 문자열에서 변환할 수 있다.

3. 진법

  • 인간은 연속적인 사고를 하지만, 컴퓨터는 이를 이산적으로 사고한다.
    즉, 컴퓨터와 인간은 사고 체계가 다르다.

  • 인간은 10진법 개념에 익숙하지만, 컴퓨터는 2진법 체계로 이해하기 때문에 인간이 가진 정보를 컴퓨터에 전달하려면 2진법적으로 풀어서 설명해줘야 한다.


10진법과 2진법

  • 물론 컴퓨터가 10진법으로 이해하면 전달이 편해지겠지만 컴퓨터의 신호, 곧 전기를 10단계로 나누어서 전달하는 것은 불안정하기 때문에 0(신호X), 1(신호O)로 전달하는게 더 안정적이다.

따라서 인간의 정보를 컴퓨터는 2진법으로 처리하여 저장한다.

int age = 25; // age : 25 -> age 11001

비트(bit)와 바이트(byte)

위 코드를 보면 10진 숫자 25가 컴퓨터에서는 2진수인 11001로 저장된다.

  • 저 숫자 하나 하나가 메모리를 차지한다 생각하면 10진법으로 2자리면 되는 걸, 2진수로 5자리나 차지하기 때문에 비효율적이다.
    때문에 후술할 8진법과 16진법을 통해서 해당 공간을 더욱 효율적으로 사용한다.

이보다 앞서서 이해해야하는 것은 컴퓨터가 공간을 구분하는 단위이다.

  • 11001(2)11001_{(2)}의 한자리는 1bit이다. 그리고 1bit 8개를 묶어서 1byte라는 단위로 사용한다.

  • 추가적으로 word라는 단위가 있는데 이는 ‘CPU가 한 번에 처리할 수 있는 데이터 크기’를 의미한다.

그러면 n개의 비트로 몇 개 10진수 값을 표현할 수 있을까?

기본적으로 공식은 쉽다.

  • 값의 개수 : 2n2^n
  • 값의 범위 : 0 ~ 2n−12^{n-1}

당연한 얘기이겠지만 개수와 범위는 잘 파악해둬야 한다. 범위는 0을 포함하기 때문에 최대값에서 –1을 해줘야 한다.


8진법과 16진법

  • 앞서말한 것처럼 2진수로만 처리하면 자리가 길어진다. 곧 공간이 커진다.
    때문에 8진법과 16진법을 통해 공간을 효율적으로 사용해준다.

  • 왜 8진법과 16진법인지 궁금하다면 답은 간단하다. 8은 232^3, 16은 242^4이다.
    따라서 2진수를 3자리 또는 4자리씩 끊어서 해당 진법으로 변환할 수 있다.


2진수를 8진수, 16진수로 변환

  • 각 자리별로 2진법의 단위에 따라 0or_{ or }1 x 2n2^n으로 곱한 뒤, 더해주면 변환된 진법의 수가 나온다.

1254(8)_{(8)} = 1 x 838^3 + 2 x 828^2 + 5 x 818^1 + 4 x 808^0 = 512 + 128 + 40 + 4 = 684
2AC(16)_{(16)} = 2 x 16216^2 + A(10) x 16116^1 + C(12) x 16016^0 = 512 + 160 + 12 = 684


정수와 진법 변환


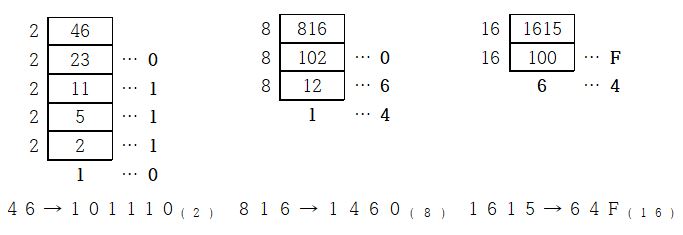
10진수를 n진수를 변환

  • n진수를 변환하는 방법은 간단하다.
    n으로 나눌 수 없을 때까지 ( n보다 작을 때까지 나눠주면 된다. ) 나눠준다.


n진수를 10진수로 변환

  • 변환된 값을 곱해서 모두 더해주면 된다. 시작은 마지막 자리(n0n^0)부터 시작한다.


실수의 진법 변환

10진 소수점수를 2진 소수점수로 변환

10진 소수를 2진 소수점수로 구하는 방식 역시 그리 어렵지 않다.

① 10진 소수에 2를 곱한다.
  0.6250.625 x 22 = 1.251.25

② 위 결과에서 소수부분만 가져다가 다시 2를 곱한다.
  0.250.25 x 22 = 0.50.5

③ 위 두 과정을 소수부가 0이 될 때까지 반복한다.
  0.50.5 x 22 = 1.01.0

  0.6250.625 → 0.101(2)0.101_{(2)}

다만 유의할 건 해당 작업이 길어지거나, 무한반복이 될 수 있다. 이 때문에 실수형에서 정밀도가 중요한 것이다.


2진 소수점수를 10진 소수점수로 변환

  • 이 역시, 2진수를 10진수로 변환하는 방법처럼 곱해주고 더해주면 된다.
    다만 단위가 소수이기 때문에 2−n2^{-n}으로 각 자리를 곱해준다는 것이다.
    (시작은 2−12^{-1}이다.)

0.101(2)0.101(2)
→ 1 x 2−12^{-1} + 0 x 2−22^{-2} + 1 x 2−32^{-3}
 = 1 X 0.5 + 0 x 0.25 + 1 x 0.125 = 0.625


음수의 2진 표현

MSB를 사용한 표현

그렇다면 2진수로 음수는 어떻게 표현할까?

  • 방법은 간단하다. n개의 비트가 표현할 수 있는 값의 개수는 2n2^n개, 범위는 00 ~ 2n−12^{n-1}까지니까 4bit면 0~15까지 표현이 가능하다.

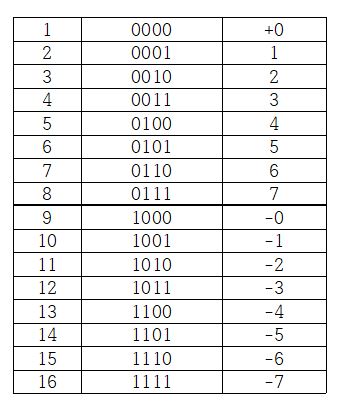
  • 여기서 4개의 비트 중 가장 좌측에 있는 비트(MSB)를 부호로 사용하게 되면, 음수까지 표현할 수 있다.
    즉, 실제 숫자는 4개의 비트 중 우측부터 3개만 표현하고 제일 좌측에 있는 비트가 부호를 표현한다.
    (0 : 양수 / 1 : 음수)

그러나 이 방식의 문제점은 0이 2개나 존재한다는 것이다. 양수 0과 음수 0으로 말이다. 이러면 결국 표현할 수 있는 값을 하나 포기하는 꼴이다.

그러니 극한의 이익을 추구하는 우리는 다른 방법을 찾아냈는데, 바로 “2의 보수법”이다.

2의 보수법

  • 2의 보수법은 보수법과 자리올림(carry)으로 발생하는 비트를 버리는 방식을 활용해서 표현한다.
  • 먼저 n의 보수란 ‘더했을 때, n이 되는 수’를 의미한다.
    예를 들어 10에 대한 7의 보수는 3이다. 이처럼 2의 보수도 더해서 2가 되는 수를 말한다.
  • 다만 우리는 2진법의 관점에서 이를 보기 때문에, 더해서 2가 되는 수란 ‘10(2)10_{(2)}’, 곧 자리올림이 발생하고 0이 되는 수다.

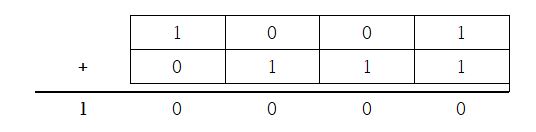
위 수에서 1001(2)1001_{(2)}은 9, 0111(2)0111_{(2)}은 7이다. 그래서 둘이 더하면 16이 나온다. 하지만 2의 보수법에서는 둘이 더해서 발생한 1(굵은 글씨)을 버린다. 이렇게 되면 실제로는 둘이 더함으로서 0이 되어버린 상황이 발생한다.

결과적으로 0111(2)0111_{(2)}은 7이 아닌 –9이다. 이게 바로 2의 보수법이자, 컴퓨터가 뺼셈하는 하는 방식이다.


음수를 2진수로 표현하기

  • 앞서 본 방식을 그대로 차용하여서 음수를 2진수로 표현하는데, 일단 부호를 보는게 아니라 절대값만 보면 된다.

   ① 절대값만 차용

    −9-9 → 99

   ② 2진수로 변환

    99 → 1001(2)1001_{(2)}

   ③ 2의 보수법으로 음수 표현

    1001(2)1001_{(2)} → 0111(2)0111_{(2)}


  • ③번을 더 쉽게 하는 방식은 ‘1의 보수법’을 사용하는 것이다.

    일단 2진법의 관점에서 진행한 것만 유의한다면, 1의 보수는 더해서 1이 되는 걸 의미한다. 그래서 1의 보수법은 0→1, 1→0으로만 변환하면 된다.

  • 그렇게 되면 1001(2)1001_{(2)}의 1의 보수는 0110(2)0110_{(2)}가 된다. 각 자리값마다 반전시켜준 것이기 때문이다. 여기서 더하게 되면 당연히 1111(2)1111_{(2)}이 된다.

  • 마지막으로 +1을 해주게 되면 자동으로 각 자리마다 올림이 발생한다.
    따라서 2의 보수는 ‘1의 보수 + 1’이다.

4. 기본형(primitive type)

이번엔 기본형의 저장방식을 살펴보자

논리형 boolean

  • 논리형은 ‘boolean’ 하나로 저장되는 값은 true, false 두 개 밖에 없다.
    따라서 1bit만 사용된다. 기본값은 ‘false’이며, 대소문자가 구분되므로 대문자 사용시 에러가 난다.

문자형 char

  • 문자형도 ‘char’만 있지만, 앞서 말했듯 char도 실질적으로 정수형이다.

    즉, 컴퓨터에 저장되는 값은 문자가 아닌 숫자가 저장되는데, 이는 ‘부호 없는 정수형’으로 0~2162^16-1까지 값을 지정할 수 있다.

여기서 char는 각 수에 대칭되는 문자 코드들이 있는데 대표적으로 ‘유니코드’가 있다.

유니코드의 문자는 그에 대칭되는 수가 있으며 char는 그 수를 저장하는 것이다.

char ch = ‘A’; // ch = 65

그래서 char는 int형으로 형변환이 가능하다.

int code = (int)ch; // code = 65

또한 16bit이기 때문에 값은 16진법으로 저장된다. 앞서 본 유니코드 65는 0x41로 우리가 10진수로 이해하기 쉽게 표현된다.


￮ 요약

  • char는 정수형이며, 그 수에 대칭되는 문자가 있다.
  • 이를 표로 만든게 유니코드이다.
  • 문자를 컴퓨터가 이진수로 변환하는 것을 ‘인코딩’ 반대를 ‘디코딩’이라고 한다.

정수형

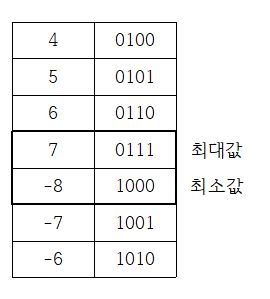
  • 정수형의 기본값은 ‘int’타입이다. 전체 비트 중에서 가장 좌측은 부호를 의미한다.

최대값과 최소값은 −2n−1-2^{n-1} ~ 2n−1−12^{n-1}-1으로 알 수 있다.


부호 없는 정수형의 오버플로우

  • 각 타입마다 해당된 만큼 비트를 가지고 있다.
    이때 그 비트를 벗어나는 경우, 즉 자리 올림이 발생하면 오버플로우가 일어난다.

오버플로우는 다음과 같다.

부호 있는 정수형의 오버플로우

  • 부호가 없는 정수가 최대값을 넘어서게 되면 발생하는 것과 달리, 부호가 있을 땐 그 시점이 “부호 비트가 변경될 때 발생한다.”
    곧 비트의 자리 올림이나, 내림이 발생하게 되면 발생한다는 것이다.

2의 보수법으로 표현된 이진수를 보면 다음과 같다.


실수형

  • 앞에서부터 계속 거론했듯이, 실수형의 포인트는 ‘정밀도’이다.
    즉, 소수점 이하 몇 번째까지 정확하게 표현하는지가 중요한 것이다.

  • 이 정밀도가 중요하게 된 이유는 앞서 본 10진법 소수를 2진법 소수를 바꾸는 과정 때문에 발생한다. 그 과정에서 무한하거나, 아니면 타입의 저장공간보다 길어질 수 있기 때문에 이를 이진수로 변환하는 과정에서 정확하게 저장하는 것이 중요하다.

참고로 실수형에서는 오버플로우가 발생하면 순환이 아닌, 무한대가 되며, 양의 최소값보다 작은 값이 되는 경우 0이 된다.

실수형의 저장형식

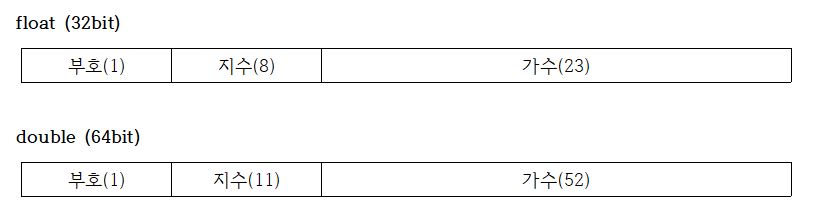
  • 실수는 비트를 부호, 지수, 가수 이렇게 3가지로 구분하여서 저장한다.
    정수형과 다르며, 실제 저장되는 형태는 2진법 형태라는 걸 유의하며 보자.

① 부호부(S)

  • 정수와 똑같이 0은 양수, 1은 음수이다.

② 지수부(E)

  • 각 단위가 2의 지수인 ‘2의 제곱을 곱한 형태(가수 x 2지수2^{지수})’로 저장하기 때문에 지수를 나타내야 한다. 이 지수는 부호가 있는 수이며, 계산 방식은 bias을 이용해서 음수와 양수를 나타낸다.

bias?
먼저 8bit가 표현 가능한 수의 개수는 256(282^8)개이며, 범위는 0~255이다. 그러나 지수는 정규화에 따라 양의 지수, 음의 지수로 구분될 수 있다. 하지만 지수부에는 부호가 따로 존재하지 않기 때문에 bias를 사용한다.

  • 즉, 0~255의 중간값(-127, 128 제외, 예약된 값이 있음)인 127를 기점으로 음수와 양수가 나뉜다. 그래서 저장할 때는 실제 지수 +127을 해준 다음, 2진수로 변환하여 저장한다.

    결과적으로 지수를 나타내기 위해선 지수부에 입력된 값에 –127을 해줘야 해당 지수가 나타난다.

   01111111(2)01111111_{(2)} => 127-127 = 202^0


￮ 요약

  • 부호가 없기 때문에 bias를 통해서 지수의 부호를 구분한다.
  • −127-127과 128128은 예약된 값이 있어서 범위에서 제외된다.
  • −127-127 : 0 / 128128 : Infinity(무한)
  • 지수가 0을 표현할 때는 –127으로 가수부도 모두 0으로 채운다.
  • double의 bias는 1023이다.

    bias시뮬레이션 https://www.h-schmidt.net/FloatConverter/IEEE754.html


③ 가수부

  • 가수부는 실제 값을 저장하는 부분으로 23bit로 7자리의 10진수를 저장할 수 있다.
    그리고 7자리의 10진수가 float의 정밀도를 나타낸다.
    때문에 float의 2배 정도 가수부가 큰 double의 정밀도가 15자리가 되는 것이다.

  • 그러나 실수 중에는 파이 같은 무한 소수, 또는 비트보다 긴 2진수 소수가 나올 수 있다.
    때문에 가수부 저장은 “정규화”라는 과정을 거친다.

  9.12345679.1234567 → 1001.000111111001101011011011...1001.000111111001101011011011...

  • 위 수가 비트를 넘기는 수 중에 하나이다.
    이를 저장하기 위해서 정규화를 사용하면 실수가 1로 시작하도록 소수점을 앞으로 옮긴다..
    이때 당기는 횟수를 ‘지수’라고 생각하는 편할 것이다.

    지수가 양수일 수록 큰 수, 음수일 수록 0에 가깝다.

  • 그래서 총 3번 옮겨야되기 때문에 정규화되면 다음과 같이 표현할 수 있다.

  1.00100011111100110101101...1.00100011111100110101101... x 232^3

  • 여기서 실수의 시작은 무조건 1이기 때문에 소수점 이하 23자리는 모두 저장할 수 있다.

￮ 요약

  • 실수형에는 오차가 존재하는데, 버려지는 비트의 시작이 1일 경우 반올림이 발생하기 때문이다.

5. 형변환

형변환(캐스팅)이란?

  • 형변환이란, 변수 또는 상수의 타입을 다른 타입으로 변환하는 것
  • 모든 변수와 리터럴에는 타입이 존재한다.
    하지만 실제로 보면 타입에 상관없이 연산이 해야되는 경우도 존재한다.
    그래서 연산 수행 전에 타입을 일치시켜야 하는데 이를 ‘형변환’이라고 한다.

형변환 방법

  • 형변환 대상 앞에 (타입)을 붙여주면 된다. 물론 이 때, 저장된 값 자체는 변하지 않는다.
double di = 85.4;
int score = (int)d;

￮ 요약

  • boolean 타입을 제외하곤 기본형의 모든 형은 변환이 가능하다.
  • 실수형에서 정수형(int)로 형변환하면 소수점 이하는 버려진다. 단, 반올림은 발생하지 않는다.

정수형 간의 형변환

  • 사실 작은 타입을 큰 타입으로 변환하는 건 딱히 상관이 없다.
    산술변환이 일어나 자동으로 타입을 처리하기 때문이다.
    다만 문제는 큰 타입을 작은 타입으로 변환할 때 일어나는데, 그 이유는 저장공간의 크기가 다르기 때문이다.

￮ 요약

  • 작은 타입에서 큰 타입으로 변환하는 경우, 남는 비트는 음수이면 1로 양수면 0으로 채운다.

실수형 간의 형변환

  • 실수형 역시 정수형과 동일하게 큰 타입을 작은 타입에 집어넣으면 값 손실이 일어난다.
    때문에 애초에 넣을 때, 큰 곳에 넣어주는 것이 정확한 값을 저장할 수 있다.

아래 코드 같은 경우, 형변환을 했지만 이미 값을 집어넣으면서 오차가 발생했기 때문에 형변환을 하더라도 값이 바뀌지 않는다.

float f = 9.1234567f; // 9.123456954956055000
double d = 9.1234567; // 9.123456700000000000
double d2 = (double)f; // 9.123456954956055000

앞서 말한 버려진 비트에서 반올림이 일어난 경우이다.

정수형과 실수형간의 형변환


정수 → 실수

  • 정수를 실수를 바꾸는 것은 간단하다.
    정수를 2진수로 바꾼 뒤, 정규화 후 그대로 실수의 저장 방식에 따라 저장하면 된다.
    다만 2진수로 바뀌는 과정에서 비트가 버려지면 반올림이 발생해 정밀도가 떨어지게 될 수도 있다는 것만 주의하자.

실수 → 정수

  • 실수를 정수로 바꾸면, 소수점 이하를 버려버린다.
    애초에 저장방식이 다르니 당연한 얘기이다.
    이때 중요한 것은 버려질 때, 반올림은 발생하지 않는다.

   1.001000111111001101011011.00100011111100110101101 x 232^3 → 1001.000111111001101011011001.00011111100110101101 → 99

방식은 역정규화를 한 다음 소수점 이하는 버리고, 정수부분만 저장한다.


자동 형변환

  • 자동 형변환이 앞서 말한 산술변환이다.
    편의상 제공하는 기능으로 컴파일러가 생략된 형변환을 추가해서 진행한다.

  • 조건은 작은 타입에서 큰 타입으로 변환할 때만 지원한다.
    반대에 경우 형변환 연산자(타입)을 생략하면 에러가 발생한다.

  • 특히 연산 과정에서 큰타입과 작은타입을 연산할 때, 자동으로 작은 타입을 큰 타입으로 변환하기 때문에 ‘산술 변환’이라 한다.

int i = 3;
double d = 1.0 + i

→ double d = 1.0 + i;
→ double d = 1.0 + (double)i;
→ double d = 1.0 + (double) 3; 
→ double d = 1.0 + 3.0; 
→ double d = 4.0;

￮ 요약

  • 컴파일러는 기존의 값을 최대한 보존할 수 있는 타입으로 자동 형변환한다.
  • 기본형과 참조형은 서로 형변환이 불가능하다.
  • 작은 타입에서 큰 타입 변환은 형변환을 생략할 수 있다.

도움이 되셨다면 '좋아요' 부탁드립니다 :)

profile
ho_c
기록을 쌓아갑니다.
다음 포스트

Ch03. 연산자

post-custom-banner

0개의 댓글