GOAL

• Heap 에 대한 이해
• 우선순위 큐에 대한 이해와 응용

1. Heap과 Heapsort

01. 정의

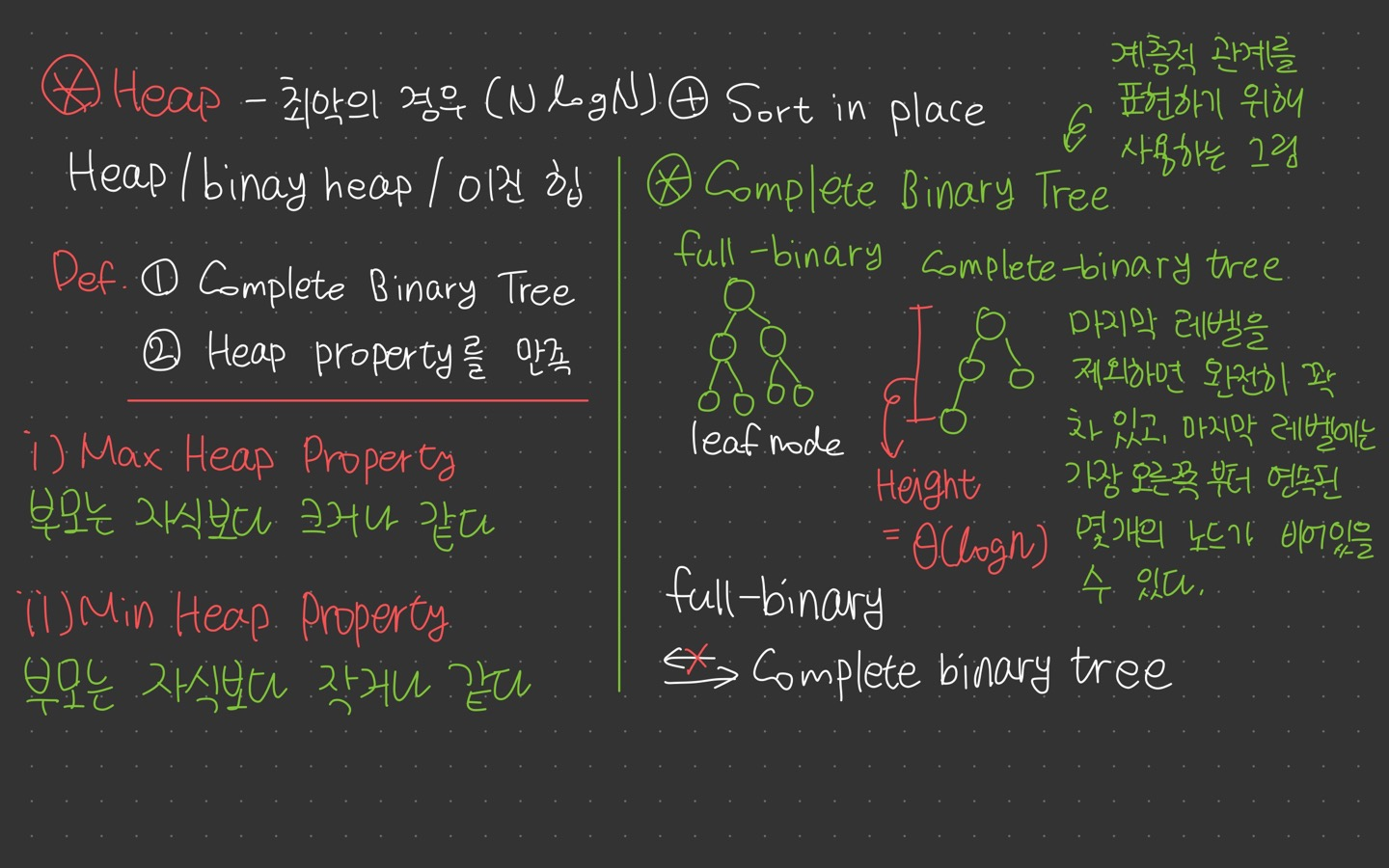
✨ Heap 은 Binary Heap 이라고도 불리는 자료구조

• 정렬에도 사용되며, 최악의 경우 시간 복잡도가 ${O(NlogN)}$
• Sort in place 로 Quick Sort나 Merge Sort와 다르게 추가 메모리를 사용하지 않음

1 ) Complete Binary Tree (완전 이진 트리) 조건을 만족

• 마지막 레벨을 제외하면 노드가 완전히 꽉 차 있고, 마지막 레벨에서는 가장 오른쪽부터 연속된 몇 개의 노드가 비어있을 수 있는 트리
• Full Binary Tree이면 Complete Binary Tree이다. (역은 성립하지 않음)

2 ) Heap Property를 만족

• a ) Max Heap Property : 부모는 자식보다 크거나 같은 값을 가진다.
• b ) Min Heap Property : 부모는 자식보다 작거나 같은 값을 가진다.

${\Rightarrow}$ 힙은 일차원 배열로 표현 가능하며, 루트는 Heap[1], Heap[i]의 부모는 Heap[i/2], Heap[i]의 왼쪽 자식은 Heap[2i], 오른쪽 자식은 Heap[2i+1] 로 표현할 수 있다.

3 ) 정리

02. Max Heapify

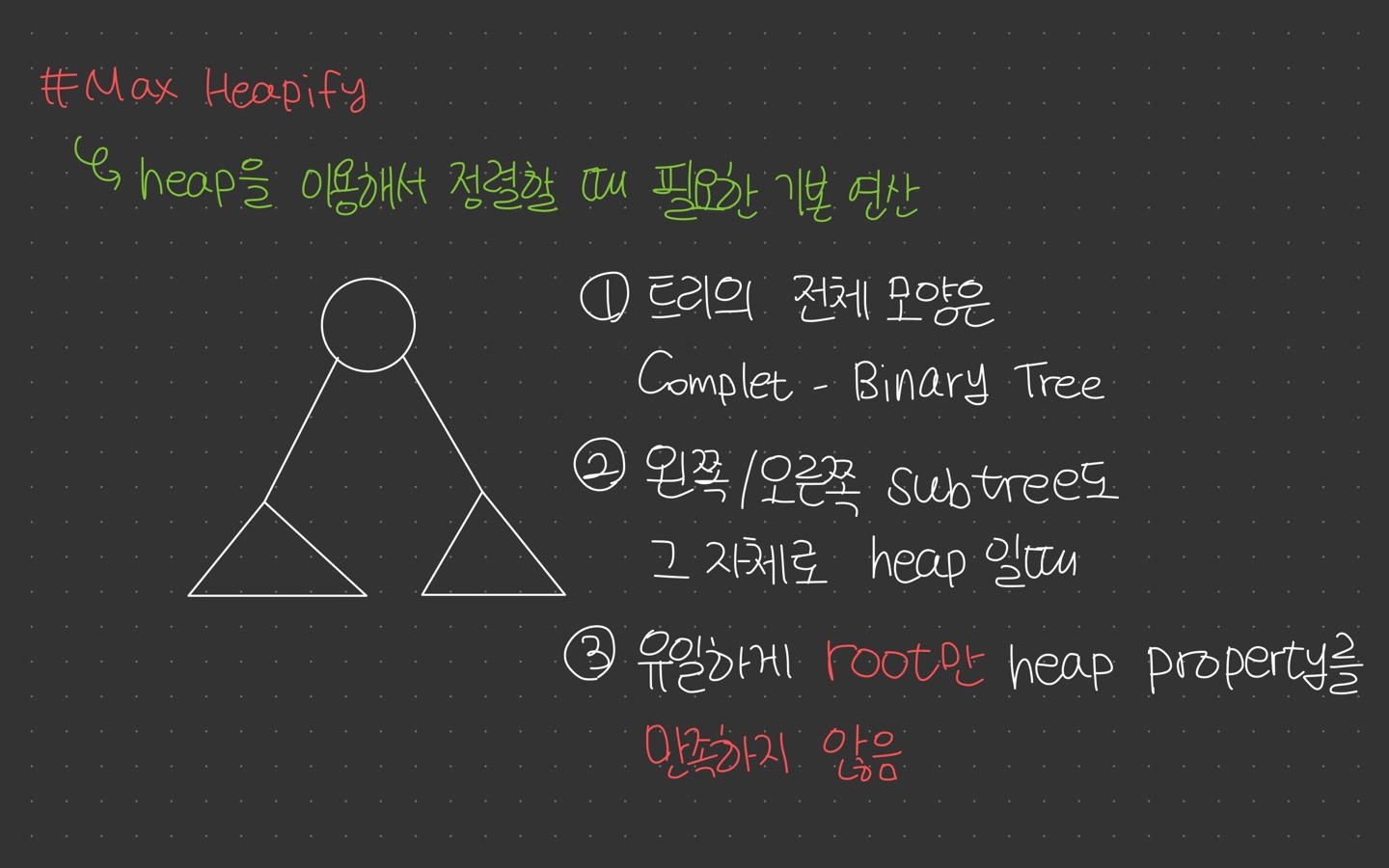
✨ Heap을 이용해서 정렬할 때 필요한 기본 연산으로 Root를 제외한 모든 Node 가 Heap Property를 만족한다고 가정

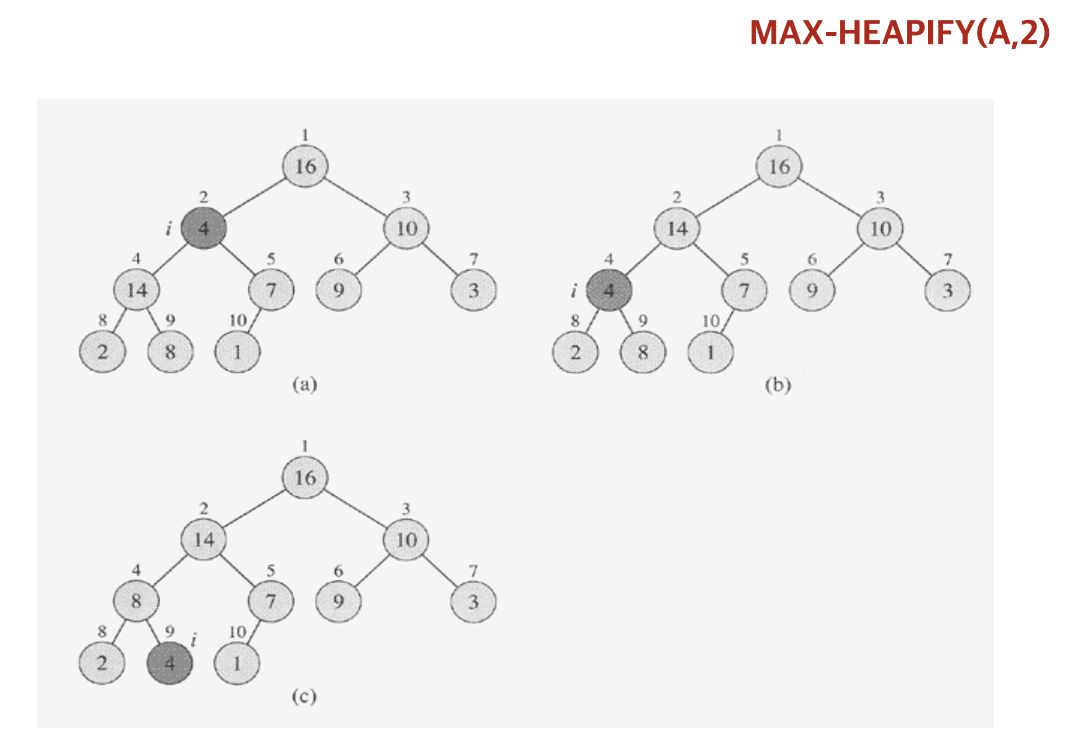
1 ) Max-Heapify Logic

• a ) Index i의 두 자식 Node 중 더 큰 값을 가지는 것의 Index 를 k 로 둔다.
• b ) 부모 노드에 해당하는 A[i] 의 값이 자식 노드 값 A[k] 보다 크거나 같을 경우, Heap Property 를 만족한다.
• c ) Heap Property 를 만족하지 않는 경우 위 두 과정을 반복한다.

2 ) Pseudo Code : Max-Heapify Recursive

Max-Heapify(A,i){
	if there is no child of A[i]
    	return;
    k <- index of **the beggest** child of i;
    if A[i] >= A[k] return;
    
    exchange A[i] and A[k];
    Max-Heapify(A,k);
}

3 ) Pseudo Code : Max-Heapify Iterative

Max-Heapify(A,i){
	while A[i] has a child do
    	k <- index of the biggest child of i;
      	if A[i] >= A[k] return;
      	exchange A[i] and A[k];
      	i = k;
    end;
     
}

4 ) 정리

03. Heap Sort

✨ 시간 복잡도: O(NlogN)

1 ) Pseudo Code : HeapSort(A)

HeapSort(A){
    build-max-heap // O(N) 주어진 데이터를 힙으로 만든다. 
    for i <- heap-size down to 2 do // N-1 번, 루트 값 (최댓값)을 맨 마지막 값과 바꾼다.
    	exchange A[i] and A[i] // O(1)
        heap-size <- heap-size - 1 // O(1) 마지막 값은 힙의 일부가 아닌 것으로 간주 (이미 정렬)
        Max-Heapify(A,1) // O(logN) Heapify 연산
}

2. 응용 : 우선 순위 큐

✨ Insert 연산과 Extract 연산으로 구성되며 시간 복잡도는 모두 O(NlogN)

01. Pseudo Code : Insertion

새로 들어온 값을 가장 마지막 노드에 추가하고 Hepify 연산을 수행한다.

Max-Heap-Insert(A,key){
	heap-size = heap-size + 1;
    A[heap-size] = key;
    i = heap-size ; // 새로 들어온 node의 index 
   while ( i > 1 and A[Parent(i)] < A[i]){
   	exchange A[i] and A[Parent(i)];
    i = Parent(i);
   }
}

02. Extract_Max

루트 노드의 값을 반환 및 제거하고 Heapify 연산을 수행한다.

• 루트 노드는 맨 마지막 노드와 swap 한 뒤 반환 및 제거

Heap-Extract-Max(A){
	if heap_size[A] < 1 {
    	then error "heap underflow"
    }
    max <- A[1]
    A[1] <- A[heap_size[A]]
    heap_size[A] <- heap_size[A] -1
    Max_Heapify(A,1)
    return max
}

3. Python의 heapq

참고

• Python document heapq

01. 주요 함수

1 ) heapq.heappush(heap, item)

• Heap의 성질을 만족하면서 item을 heap으로 push

2 ) heapq.heappop(heap)

• Heap의 성질을 만족하면서 heap에서 가장 작은 항목을 pop 하고 반환
• Heap이 비어 있는 경우, Index Error
• Pop을 하지 않고 가장 작은 항목에 접근하려면 heap[0]

3 ) heapq.heapify(x)

• List를 제자리에서 Heap으로 변환 ( O(N) )

4 ) heapq.heapreplace(heap, item)

• Heap에서 가장 작은 항목을 pop하고 반환하며, 새로운 item도 푸시
• Pop이 먼저이므로 반환된 값이 item보다 더 클 수 있음

5 ) heapq.heappushpop(heap, item)

• Heap에 item을 push한 다음 가장 작은 항목을 pop하고 반환

h = []
heappush(h, (5, 'write code'))
heappush(h, (7, 'release product'))
heappush(h, (1, 'write spec'))
heappop(h) # (1, 'write spec')

Quize

• 동일한 값이 추가되었을 때, 정렬 상태에서 값이 추가된 순서대로 유지되는 것을 stable sort라고 한다. 우선 순위 큐는 Stable Sort 인가 ?
  • 아닙니다. Stable Sort를 위해서는 값이 추가된 순서를 별도로 가지고 있는 등의 처리가 필요합니다. Stable Sort에는 Insertion,Merge,Bubble,Counting Sort가 있습니다.

02. Priority-Queue와의 비교

참고

• Stack Overflow : What's the difference between heapq and PriorityQueue in python?

Priority-Queue 에서는 heapq 를 Wrapper 하여 사용하고 있다.
Priority-Queue는 Thread Safe 하고, heapq는 Non-Safe

• Thread Safe 가 중요하지 않을 때는 heapq를 사용하는 것이 속도면에서 유리

연관 문제

• 백준 1715 카드정렬하기
• 백준 1202 보석도둑