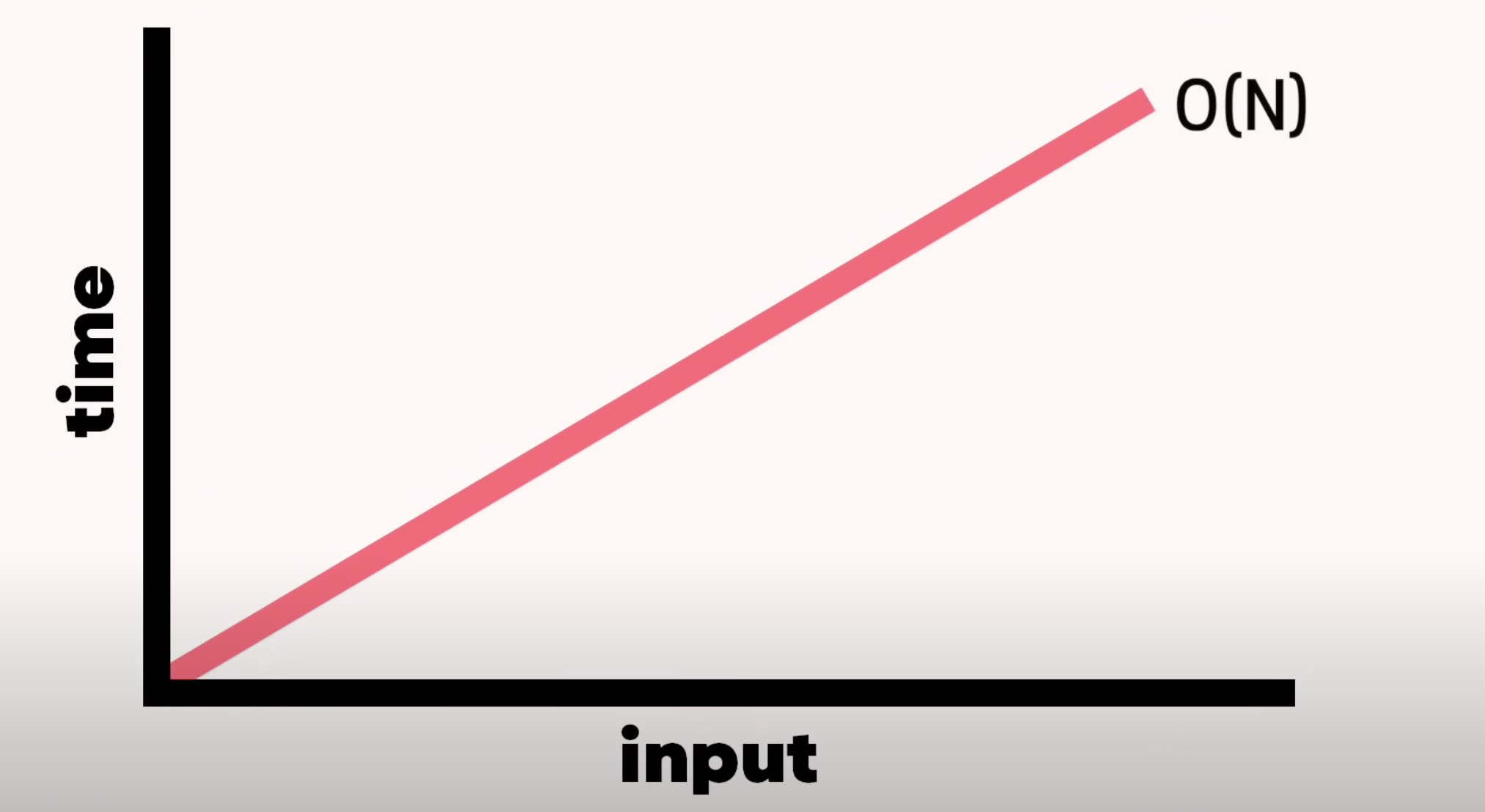
1. 선형 검색 알고리즘(Linear Search)
Time complexity = O(N)
- 배열이라면 하나씩 계속 체크
- input Size = N -> N steps
2. Constant Time(상수시간) Complexity
Time complexity = O(1)
- input N이 얼마가 됐든 항상 한 번이면 충분
- 이 함수의 time complexity는 constant time(상수 시간)
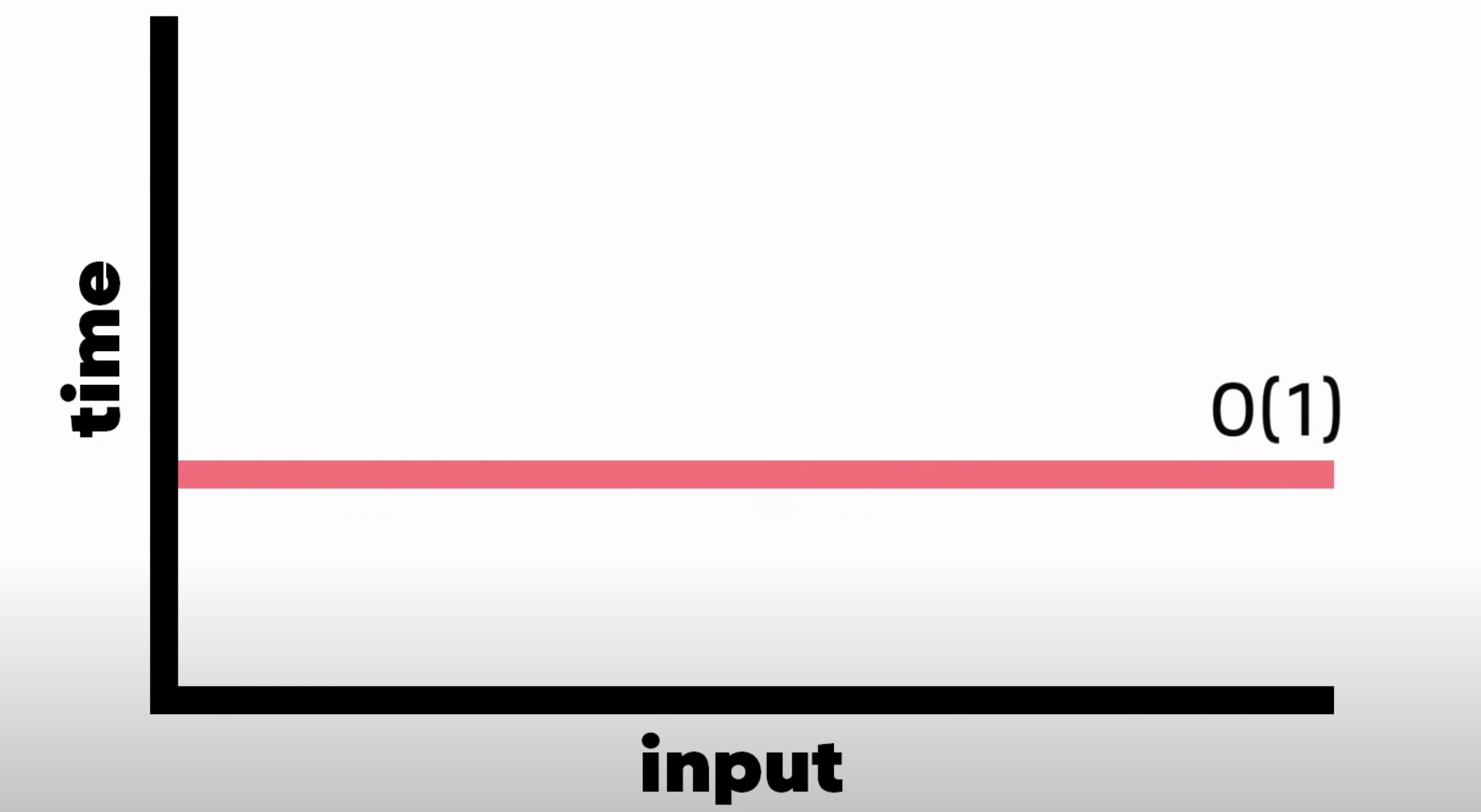
3. Constant Time Complexity 2
Time complexity = O(1)
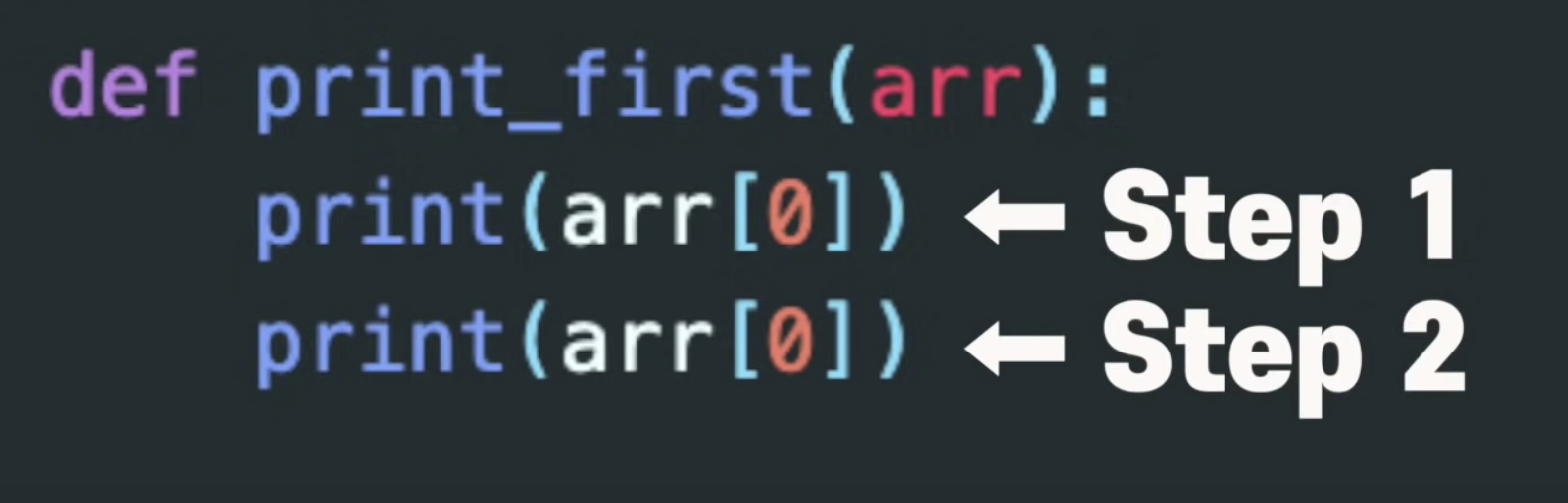
- 같은 작업을 한 번 더 해주지만 O(2) 가 아니라, Time complexity = O(1)
- Big O는 함수의 디테일에 관심이 없고, rough하게 이 함수가 인풋사이즈에 따라서 어떻게 동작하는지만 체크
Big O는 상수(constant)에 신경을 쓰지 않음
4. 반복문을 포함한 함수
Time complexity = O(N)
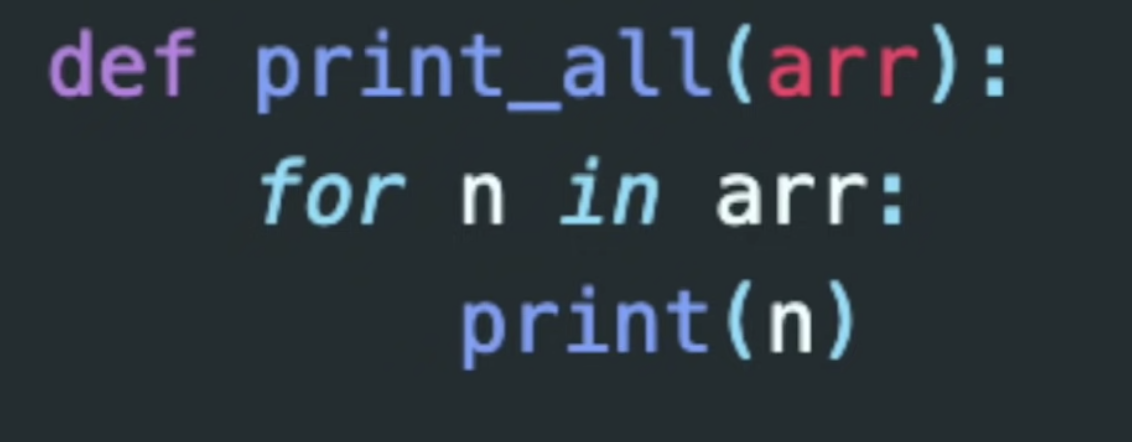
- 각각을 프린트하는 함수 => for문으로 하나씩 돌려줌 => 선형검색과 비슷
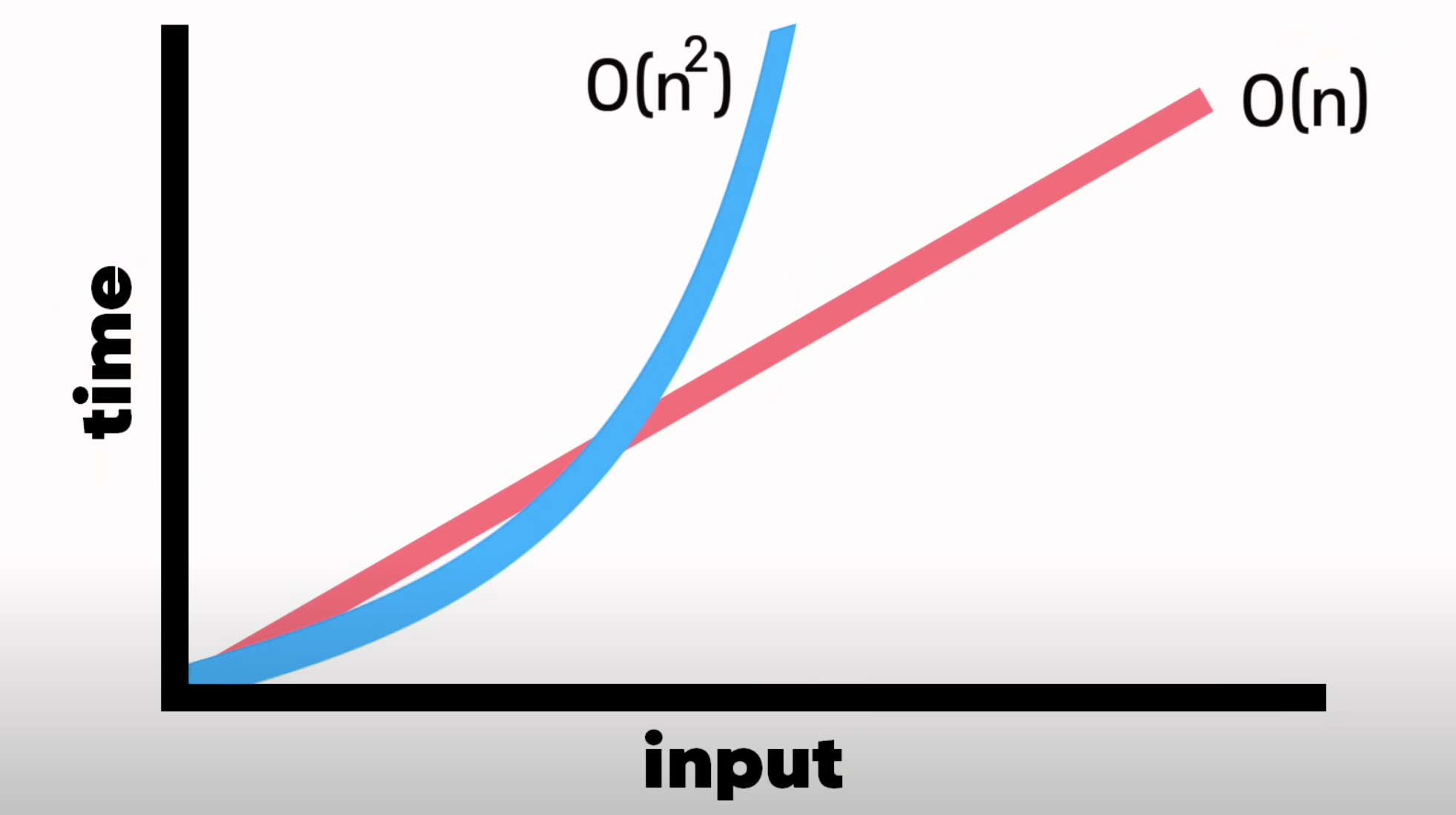
5. Quadratic Time (2차 시간)
Time complexity = O(N^2)
- Quadratic Time은 Nested Loops(중첩 반복) 이 있을 때 발생 : for문 안에 for문
- Input^2 steps가 필요
6. Logarithmic Time(로그 시간) Complexity
Time complexity = O(log N)
- Binary Search(이진 검색) 알고리즘 설명할 때 사용
- Binary Search는 각 프로세스의 스텝을 절반으로 나눠서 진행하기 때문에, input이 double이 되어도 step은 +1밖에 증가하지 않음
- 로그(logarithm)은 지수(exponent)의 정반대 개념
- '32를 2로 몇번을 나눠야 1이 나올까?'라는 문제
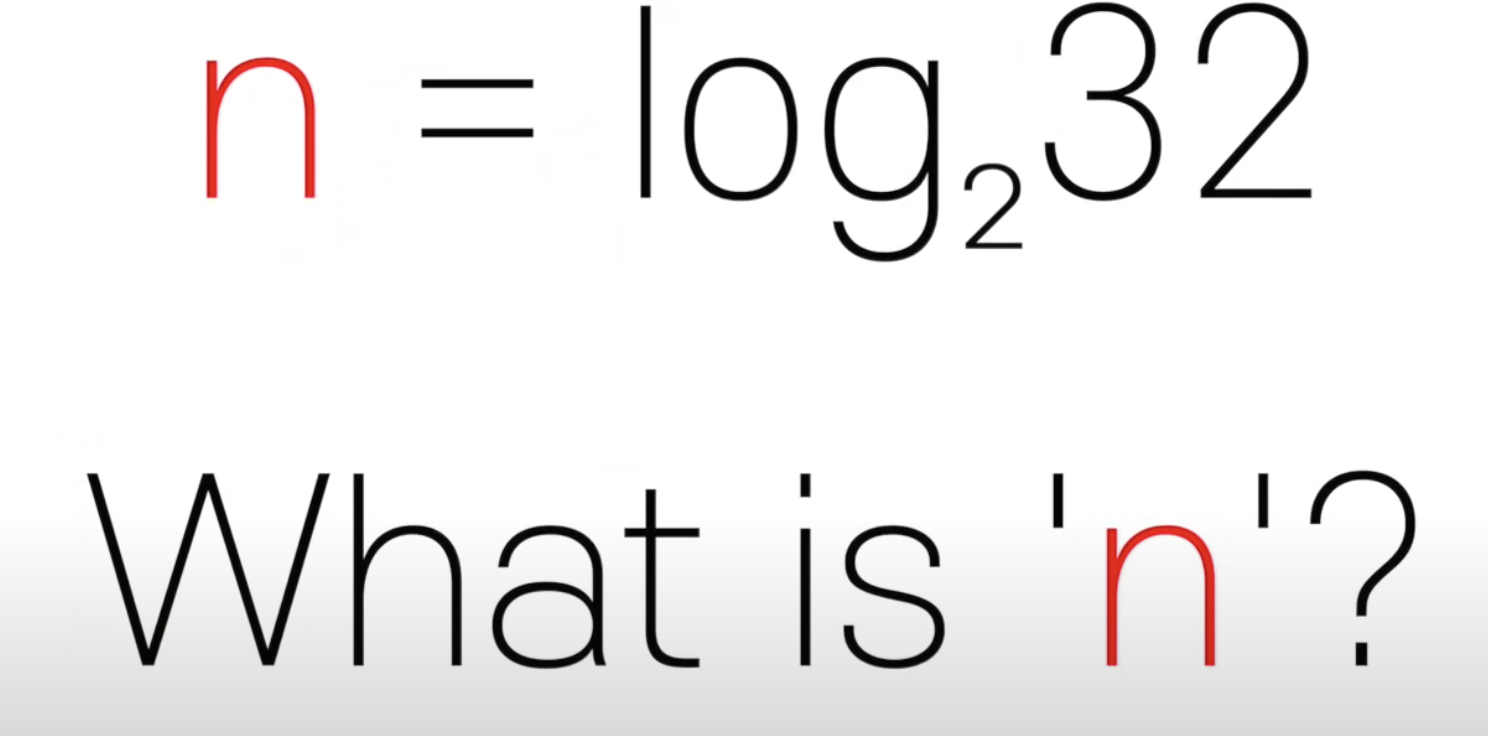
- BigO의 특성 상 Base는 쓰지 않기 때문에 '밑'은 사라지고, 몇 번 곱해져야 하는지만 남음
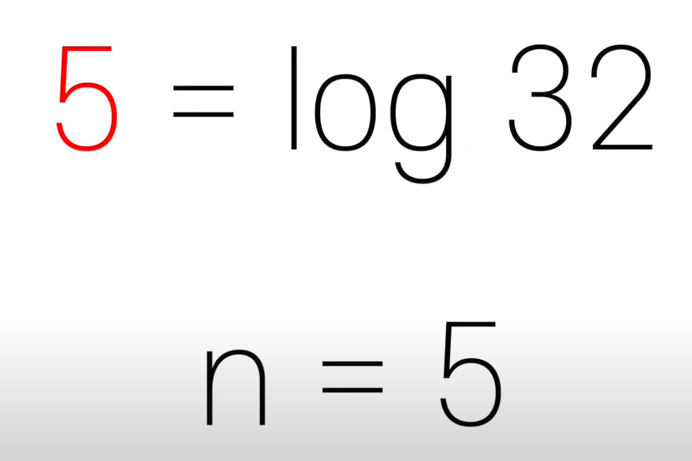
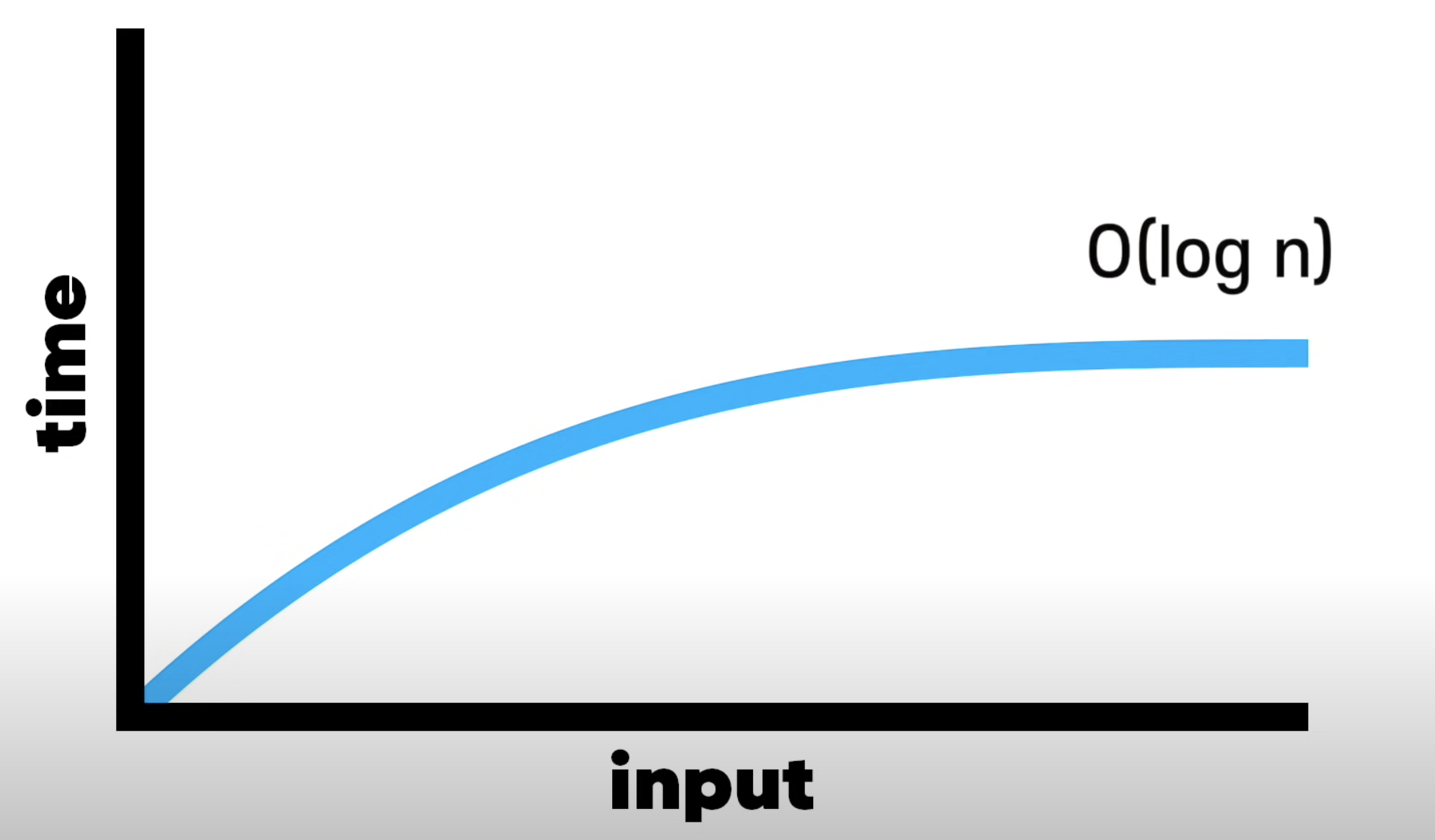
- Logarithm은 상수보다는 느리고, 선형 검색보다는 빠름
- Trade Off (상충 관계) : 이진 검색은 정렬되지 않은 배열엔 사용할 수 없음
7. Big O 총정리
- 가장 선호되는 것은 상수 시간
- 상수시간(constant) < 로그시간(logarithmic) < 선형시간(linear) < 지수시간(exponential) or 2차시간(quadratic)
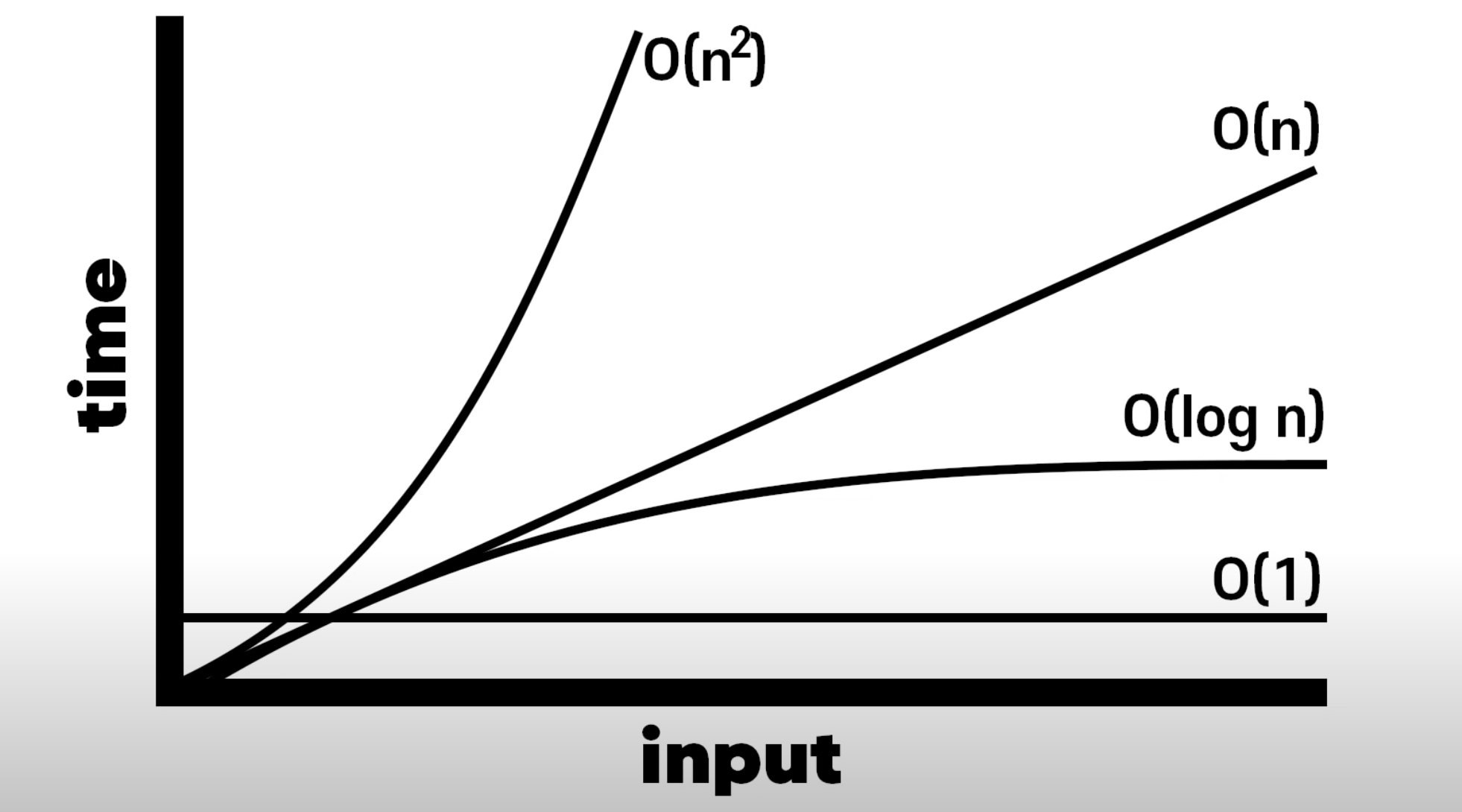
출처 : Big O 설명 by 노마드 코더
https://www.youtube.com/watch?v=BEVnxbxBqi8
