🍭 피보나치 수열(메모이제이션)

🍡 피보나치 수열을 코드로 구현해 보자

package algori.algoRecursive;

public class Fibo {

    public int DFS(int f){
        if(f ==1) return 1;
        else if(f==2) return 1;
        else return DFS(f-2)+DFS(f-1);
    }

    public static void main(String[] args) {
        Fibo fibo = new Fibo();
        int n = 7;
        for(int i=1;i<=n;i++)
            System.out.print(fibo.DFS(i) + " ");

    }
}

피보나치 수열은 아래와 같은 방법으로 전개가 된다.

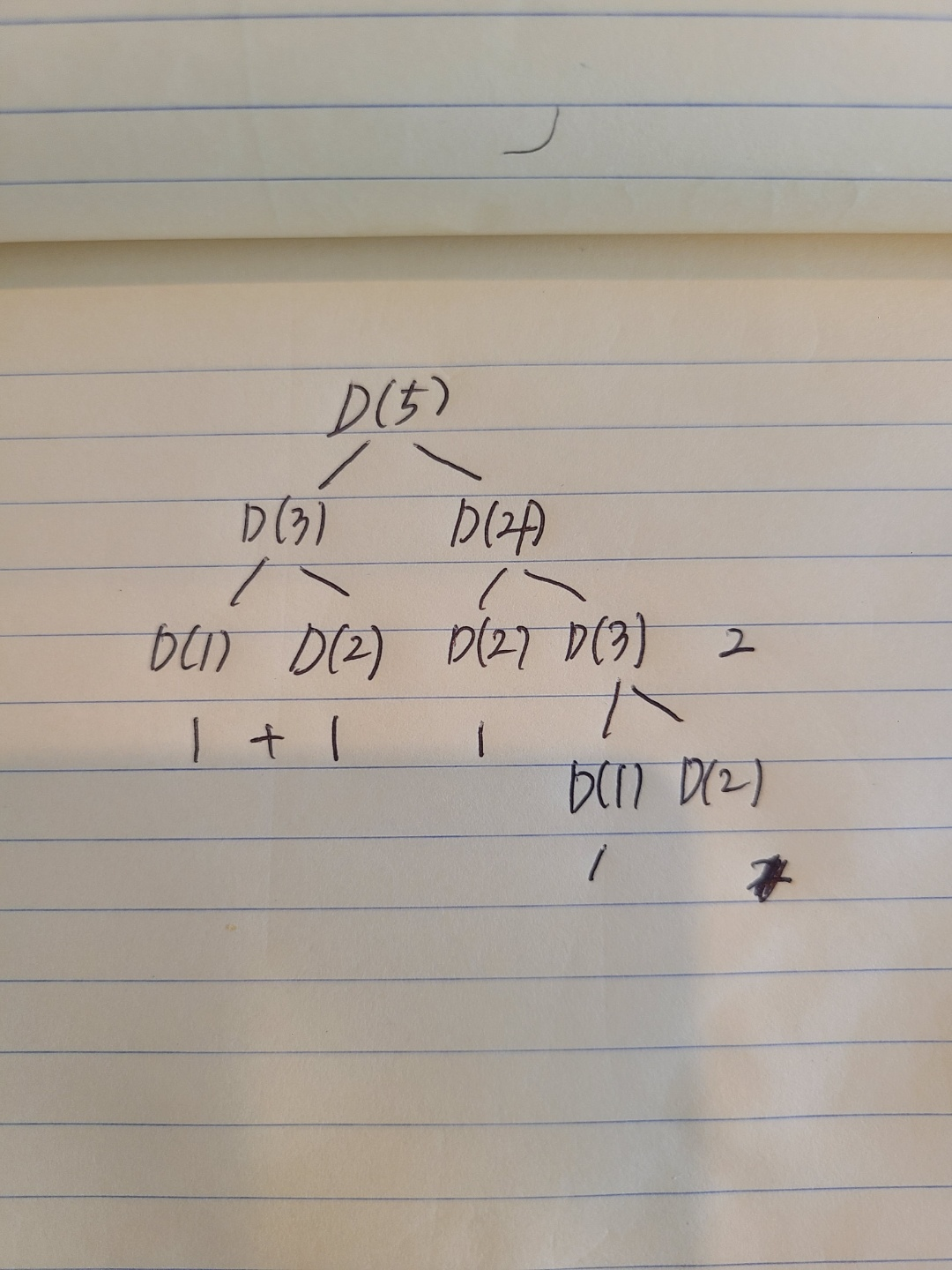
🍡 위의 코드의 문제점은 무엇일까

위의 코드는 입력값이 작으면 값이 금방 나오지만, 커지면 커질수록 시간복잡도가 높아진다.

🍮 배열을 이용해 코드를 수정해보자.

package algori.algoRecursive;

public class Fibo2 {
    static int[] fibo;
    public int DFS(int n){
        if(n==1) return fibo[n] = 1;
        else if(n==2) return fibo[n] = 2;
        else return fibo[n] = DFS(n-2) + DFS(n-1);
    }

    public static void main(String[] args) {
        Fibo2 T = new Fibo2();
        int n = 45;
        fibo = new int[n+1];
        T.DFS(n);
        for(int i=1;i<=n;i++)
            System.out.print(fibo[i] + " ");

    }
}

🍡 메모이제이션을 사용해보자

🍮 더 좋은 방법은 없을까

위의 코드의 입력값이 10이라고 하고 처리되는 과정을 그려보자.

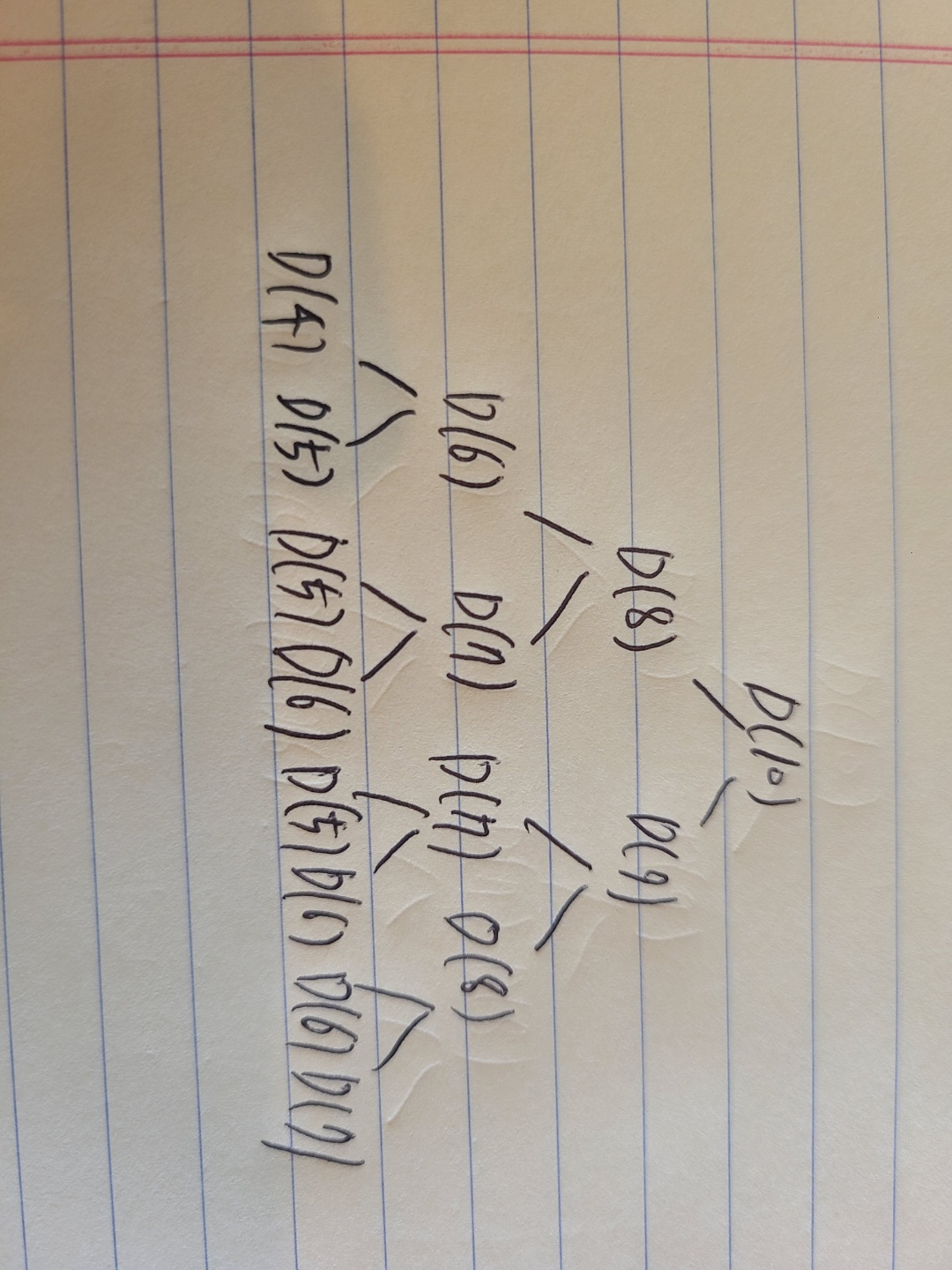
입력값이 10밖에 되지 않지만, D(6)의 값을 구하기 위해서 D(4)+ D(5)의 값을 구해야하고, D(7)의 값을 구하기 위해서 D(5),D(6)의 값을 구해야 한다.
같은 값을 기억하고 있으면 시간 복잡도를 줄일 수 있지 않을까,

if(fibo[n] > 0) return fibo[n]; 을 추가해주자.

package algori.algoRecursive;

public class Fibo3 {
    static int[] fibo;

    public int DFS(int n){
        if(fibo[n] >0) return fibo[n];
        if(n==1) 
            return fibo[n] = 1;
        else if(n==2)
            return fibo[n] = 1;
        else return fibo[n] = DFS(n-2) + DFS(n-1);
    }

    public static void main(String[] args) {
        Fibo3 T = new Fibo3();
        int n = 45;
        fibo = new int[n+1];
        T.DFS(n);
        for(int i=1;i<=n;i++)
            System.out.print(fibo[i] + " ");
    }
}

출력이 금방 되는 것을 알 수 있다!