LeetCode 141 (feat. Floyd's Cycle Detection Algorithm)

Jene Hojin Choi·2021년 4월 2일

Algorithm

목록 보기

11/17

리트코드를 풀다가, 새로운 유형의 알고리즘을 접하게 되었다. Linked List 자료구조에 대해서는 이미 공부를 해두었지만, 그것을 문제에 적용하는 법에 대해서는 잘 알지 못했었다. 또한, 포인터에 대해서도 알았지만, 다른 속도로 움직이는 포인터를 사용하는 것도 처음 알았다. 역시 알고리즘 뉴비인 나는 배울 것이 아직도 많다.

LeetCode 141.

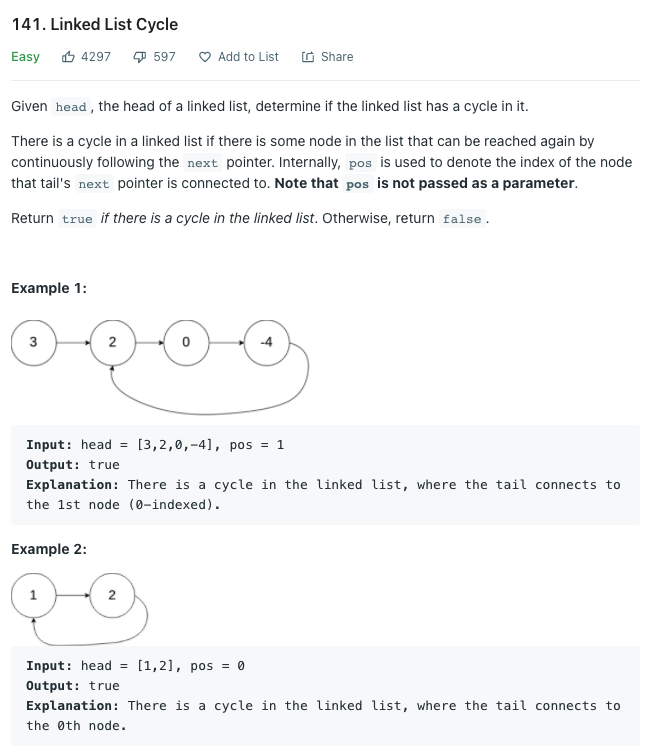
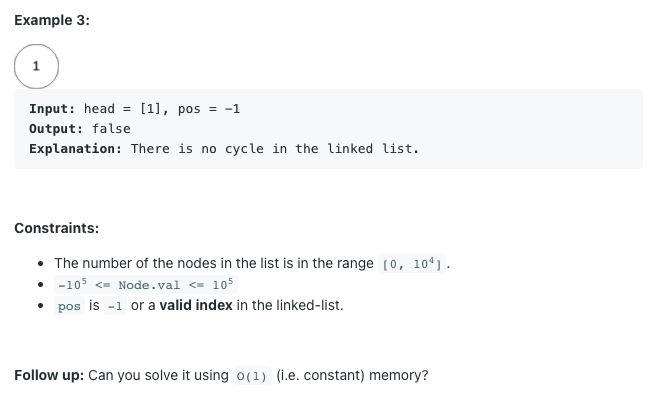
이 문제는 연결 리스트에서 반복되는 cycle이 있는지 찾는 문제이다. 있으면 True, 없으면 False를 리턴해야한다.

Solution

Approach 1. Brute and Force

Brute Force는 문제를 해결하기 위해서 모든 경우의 수를 다 생각해본다는 뜻이다. 하지만 계산해야하는 것들이 많아질 수록 시간 면에서 굉장히 비효율적인 알고리즘이 될 수 있다.

이 솔루션은 다음의 두 사실에 기반한다.

cycle이 있다면 head의 node를 차례대로 검사하다가 이미 검사했던 node를 또 만난다.
아래의 예시를 보자.
처음부터 차례대로 검사한다고 가정했을때, 순서는 3 -> 2 -> 0 -> 4 -> 2 -> 0 -> ... 이 될 것이다.
이때 2는 이미 검사한 node이므로 두번째로 같은 2를 마주쳤을때 이 linked list에 cycle이 있다는 것을 알 수 있다.

cycle이 없다면 head의 node를 차례대로 검사하다가 node는 언젠가 Null이 될 것이다. 위의 예시에서 cycle이 없다면, 맨 앞 head부터 차례대로 검사했을 때 3 -> 2 -> 0 -> -4 -> Null 이 된다.

Code

접근 방식은 다음과 같다.

인자로 받은 head의 node를 차례대로 검사하고, seen이라는 list에 저장한다.
만약 체크하는 node가 seen list에 있다면 cycle이 있고, return True를 한다.
반면에, 인자로 받은 head의 모든 node를 검사했는데도 unique한 node만 있었다면, return False를 한다.

class Solution(object):
    def hasCycle(self, head):
        if head is None:				[1]
            return False
        seen = []					[2]
        while head:					[3] 
            if head in seen:				[4]
                return True
            seen.append(head)				[5]
            head = head.next				[6]
        return False

[1] 일단 Example 3에서와 같이 head가 []일 경우는 cycle이 존재할 수 없으므로 False를 리턴한다.
[2] 만난 node를 저장하기 위한 용도로 빈 리스트를 만든다.
[3] head가 Null이 아닐때까지만 while 문을 돌린다.
[4] head가 이미 seen list에 있었다면 cycle이 존재하는 것이므로 return True를 한다.
[5] head가 seen list에 없다면 seen list에 추가해준다.
[6] head를 다음 node로 업데이트해준다.
[7] 만약 head가 None이 되면 return False를 해준다.

Time complexity, Space complexity

시간 복잡도: O(n) (head의 n elements들을 한번씩은 검사한다.
공간 복잡도: O(n) (seen list에 head의 n elements들을 한번씩은 저장한다.)

Approach 2. Fast, Slow

Floyd's Cycle Detection Algorithm

Cycle이 존재하는 linked list가 있다고 가정해보자. 맨 처음 head node부터 포인터 두개를 사용한다. 하나는 slow 포인터로, 한개씩 움직인다. 다른 하나는 fast 포인터로, 두개씩 점프한다.

Linked list가 [1, 2, 3, 4, 5, 6] 이라고 가정하자. 파란색 포인터가 slow, 노란색 포인터가 fast라고 가정해보자. 아래의 사진처럼 포인터들이 움직인다고 가정하면 둘은 언젠가는 만날 것이다!!

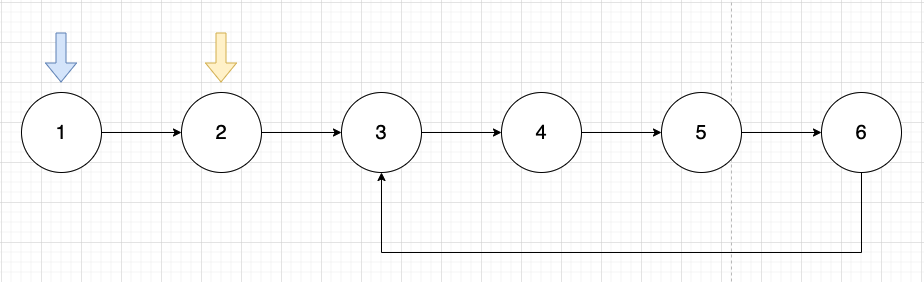
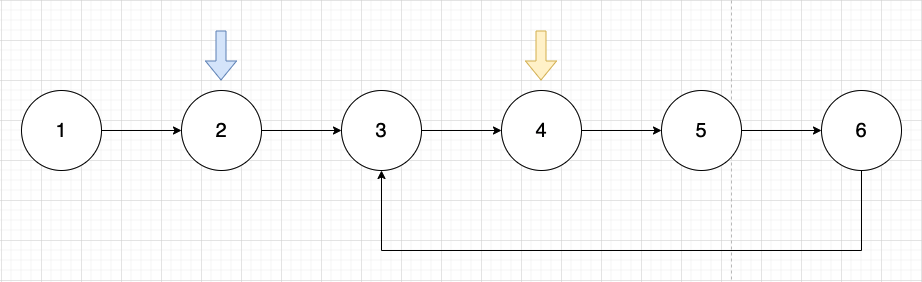
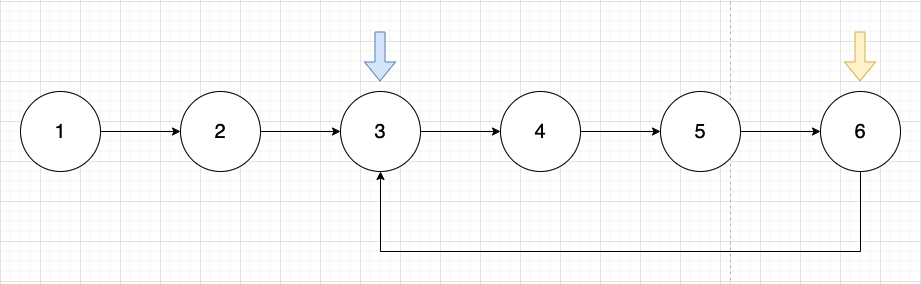
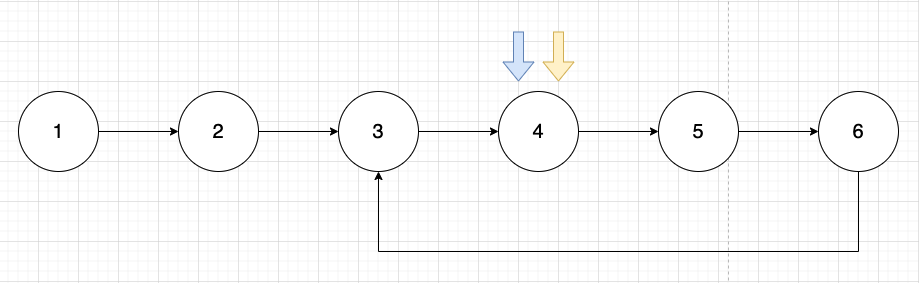
Code

class Solution:
    def hasCycle(self, head: ListNode) -> bool:
        if head is None:					[1]
            return False
        slow = head						[2]
        fast = head.next					[3]
        while slow != fast:					[4]
            if fast is None or fast.next is None:		[5]
                return False
            slow = slow.next					[6]
            fast = fast.next.next				[7]
        return True						[8]

[1] head가 none이면 cycle이 없으므로 return False한다.
[2][3] slow는 head (맨 처음 node), fast는 head의 다음 node부터 시작한다.
[4] slow, fast이 둘의 값이 다를때까지 loop를 돌린다.
[5] 만약 cycle이 없다면 fast가 제일 먼저 tail 다음인 null에 도달할 것이므로 체크하고, 만약 null이면 return False한다.
[6][7] slow, fast둘의 값을 업데이트 해준다. slow는 한번 점프, fast는 두번 점프한다.
[8] 만약 slow, fast이 같게 되어 loop에서 나오면 return True한다!

Time complexity, Space complexity

source: https://stackoverflow.com/questions/47193225/runtime-complexity-of-floyds-cycle-detection

(위에서 설명한 loop는 leetcode 141의 cycle과 같다. 나는 글의 통일성을 위해 cycle이라고 바꿔서 부르겠다.)

linked list가 N개의 node로 구성되어 있다고 가정해보자.
cycle이 없다면 fast pointer가 제일 먼저 tail 다음인 null을 찾거나, 혹은 cycle이 있다면 slow pointer가 cycle 안을 돌 것이다.

만약 cycle이 있다면 그 cycle의 길이를 M이라고 하자. M <= N일것이다.
만약 cycle 안에서 fast, slow 포인터가 만난다면 M 만큼의 node를 확인하는 것이다.

그렇다면 총 시간은 N + M <= 2N이므로, 시간 복잡도는 O(2N) = O(N)이다.