
Introduction
정렬 알고리즘은 n개의 숫자가 주어졌을때, 이를 사용자가 지정한 기준에 맞추어 정렬하는 알고리즘이다.
정렬 (Sorting)
선택 정렬 (Selection Sort)
요약
- 정렬되지 않은 배열의 맨 앞에서부터, 그 이후의 값중 가장 작은 값을 찾는다.
- 가장 작은 값을 찾으면 그 값을 현재 인덱스의 값과 바꾸어준다.
- 다음 인덱스로 넘어가고, 위의 과정을 반복한다.
Big-O : O(n^2)
삽입 정렬 (Insertion Sort)
요약
- 두번째 인덱스부터 시작한다.
현재 인덱스의 값은 별도의 변수에 저장하고, 바로 앞 인덱스의 값과 현재 인덱스의 값을 비교한다. - 만약 현재 인덱스의 값이 전 인덱스의 값보다 작다면, 전 인덱스의 값을 현재 인덱스로 옮겨준다.

Big-O
- 최악의 경우: O(n^2) (Big-O는 최악의 경우를 기준으로 생각. 고로 O(n^2))
- 이미 정렬된 경우: O(n)
안정 정렬 (Stable sort)이다. 안정 정렬이란, 중복된 값을 입력 순서와 동일하게 정렬하는 정렬 알고리즘이다. 버블 정렬, 병합 정렬 또한 안정 정렬의 종류이다.
버블 정렬 (Bubble Sort)
요약
- 매번 연속된 인덱스 두개를 비교한다. 두번째 인덱스부터 시작하여, 바로 앞 인덱스와 비교한다.
- 앞 인덱스가 더 크다면, 현재 인덱스와 값을 바꿔준다.
- 현재 인덱스가 더 크면, 값을 바꾸지 않고 다음 두 연속된 배열값을 비교한다.
Big-O : O(n^2)
안정 정렬 (Stable sort)이다.
합병 정렬 (Merge Sort)
분할 정복 알고리즘의 하나이다. 분할 정복(divide and conquer) 방법이란,
- 문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다.
요약
- 현재 열을 반으로 쪼갠다.
- 이를 쪼갠 리스트의 크기가 0이나 1이 될때까지 반복한다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.
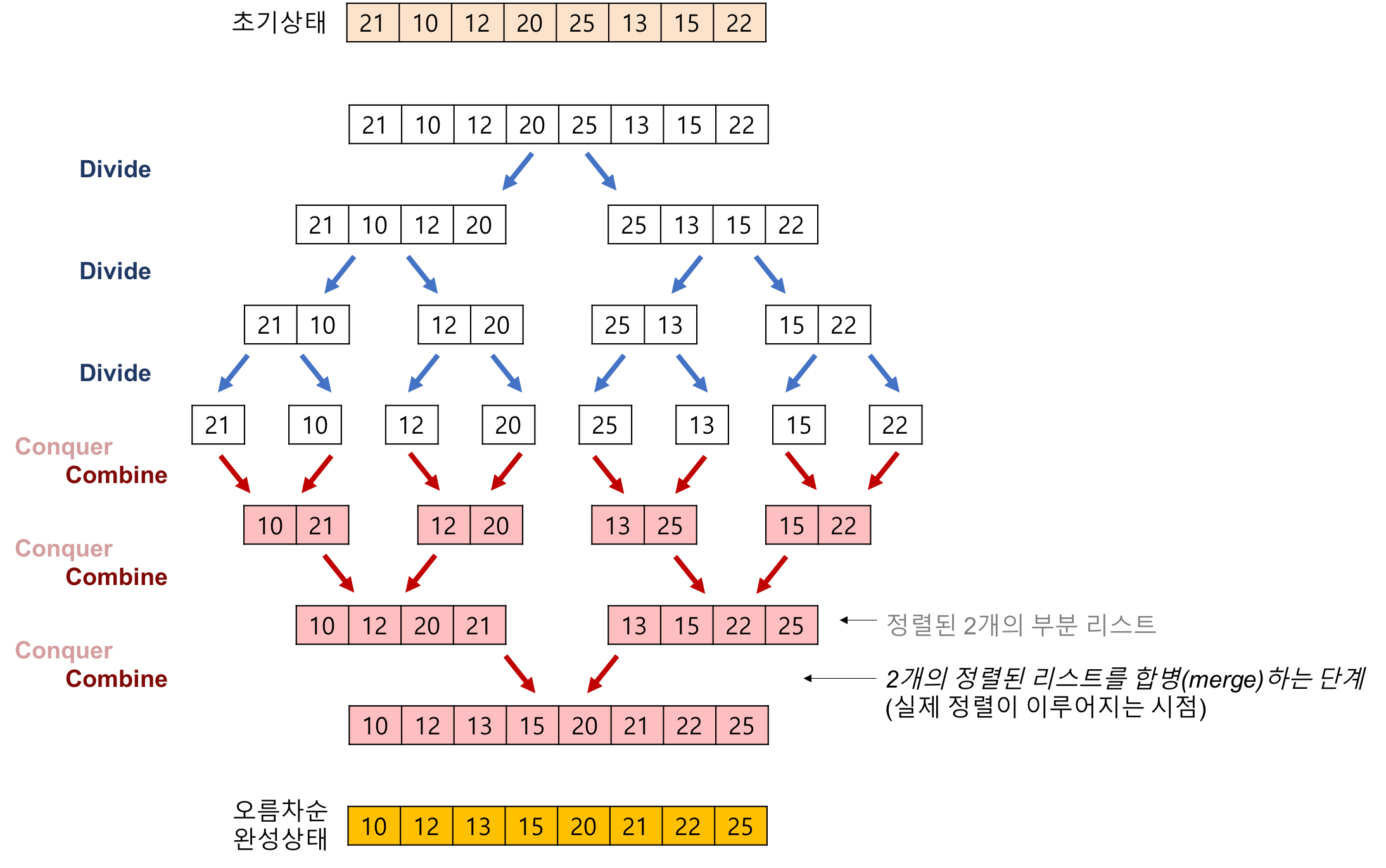
Big-O: O(nlog_2(n))
안정 정렬 (Stable sort)이다.
퀵 정렬 (Quick Sort)
불안정 정렬이다.
분할 정복 알고리즘의 하나이다.
요약
- 리스트 안의 한 요소를 선택한다. (pivot element)
- pivot을 중심으로 pivot보다 작은 요소들은 pivot의 왼쪽으로, 큰 요소들은 오른쪽으로 옮긴다.
- 2개의 인덱스 변수(low, high)를 이용해서 리스트를 두 개의 부분 리스트로 나눈다.
- pivot을 제외한 왼쪽 리스트와 오른쪽 리스트를 각각의 pivot을 정하고 이를 기준으로 정렬하는 step 1-2의 과정을 반복한다.
- 부분 리스트의 크기가 0이나 1이 될때까지 반복한다.
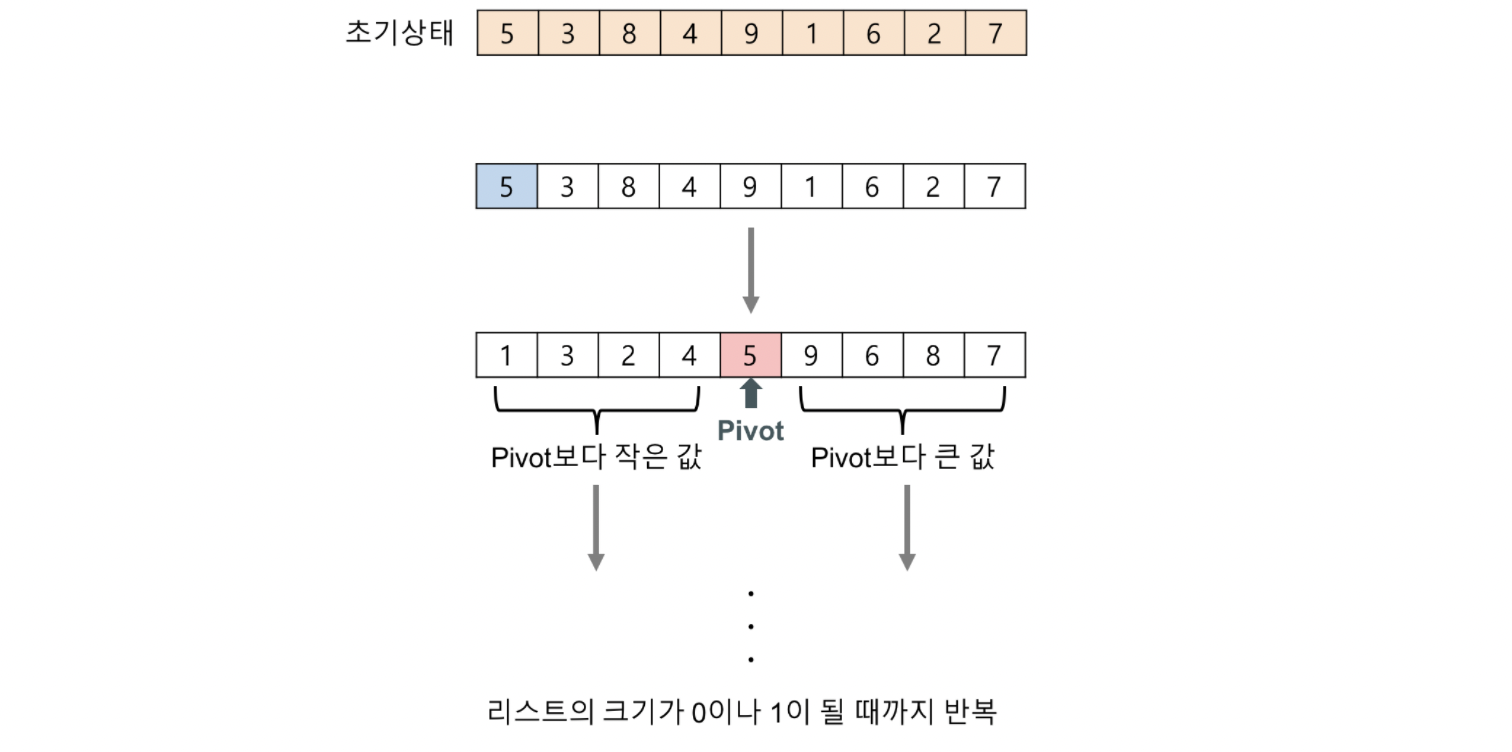
Big-O: O(nlog_2(n))
힙 정렬 (Heap Sort)
요약
오름차순 정렬을 한다면:
1. 정렬해야하는 요소들로 최대 힙(max heap) 를 구성한다.
2. 가장 큰 요소는 root에 있을 것이다. 루트 노드의 값 대신 힙의 맨 마지막 값을 넣고, 힙의 사이즈를 -1한다. (즉, 최댓값부터 삭제한다.)
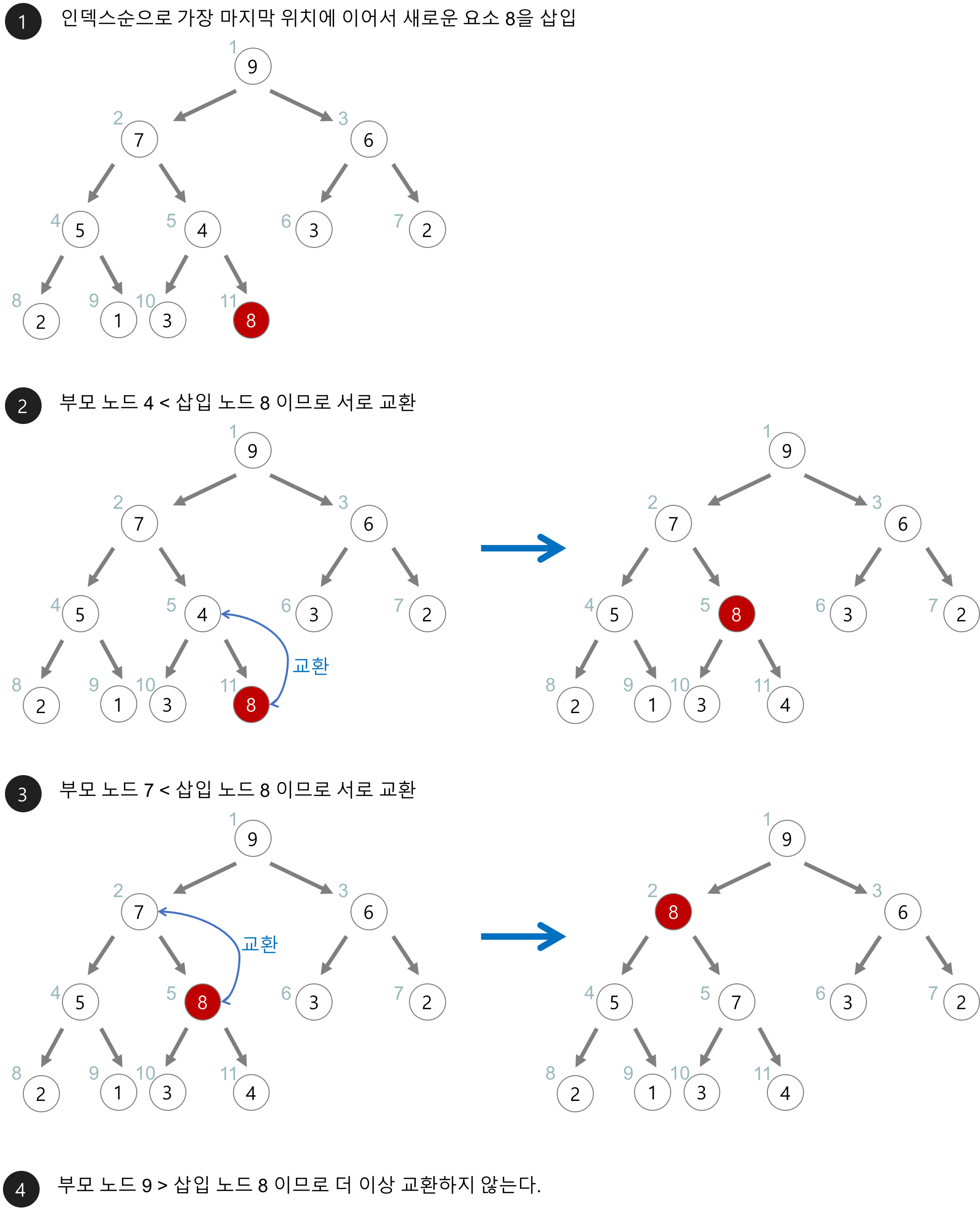
Summary
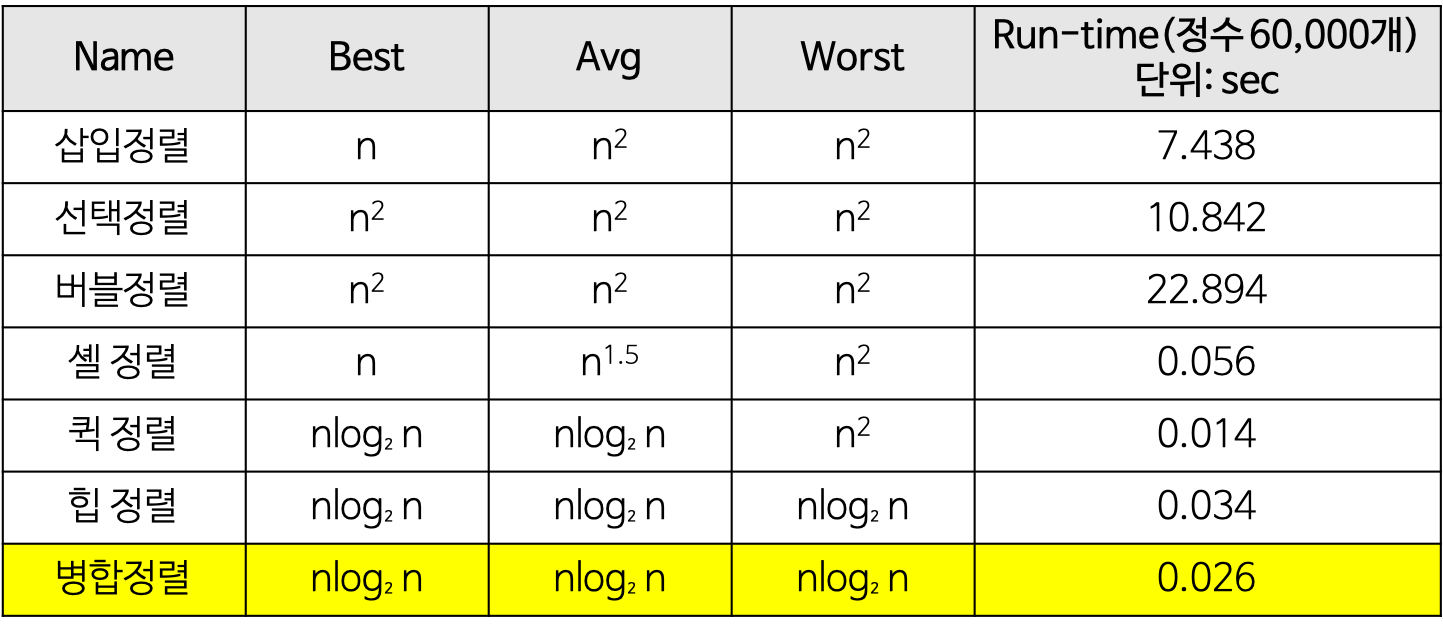
Reference
https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
