[자료구조] 시간 복잡도, 공간 복잡도

공간 복잡도(space complexity)

• 프로그램을 실행시켜 완료하는데 필요한 메모리 양
• 고정부분
  * 보통 명령어 공간, 단순 변수, 집합체, 상수를 위한 공간
• 가변 부분
  * 변수, 참조된 변수가 필요로 하는 공간, 재귀스택 공간
• 프로그램 P의 공간 요구 S(P) = c + Sp
  * c : 상수
  • Sp : 인스턴스 특성(문제에 따라 달라지는 값, 인스턴스로 인해 필요로 하는 공간)

시간 복잡도(time complexity)

• 프로그램을 완전히 실행시키는데 필요한 시간, 알고리즘에 사용되는 연산 횟수의 총량
• T(P) = 컴파일 시간 + 실행시간 Tp
• 실행시간에 주로 관심
• 프로그램 단계 수 (number of steps)
  - 주석 : 0
  • 선언문 : 0
    • 변수, 상수 정의
      • 사용자 데이터 타입 정의(class, struct, union, template)
      • 접근 결정(private, public, protected, friend)
      • 함수 타입 결정(void, virtual)
        - 함수 호출
    • 값에 의한 전달 인자 포함하지 않을 경우 : 1
    • 값에 인한 전달 인자 포함할 경우 : 값 인자 크기의 합
    • 재귀적인 경우 : 호출되는 함수의 지역변수도 고려
      - 메모리 관리 명령문 : 1
      - 함수문 : 0
    • 비용이 이미 호출문에 해당
      - 분기문 : 1
  • 산술식 및 지정문 : 1
    • 예외 : 함수 호출을 포함하는 산술식
  • 반복문 : 제어부분에 대해서만 단계수 고려
  • 스위치문
    • switch()의 비용 = 의 비용
  • if-else 문
• , , 에 따라 각각 단계수가 할당

[예시]
1. Linear Loops

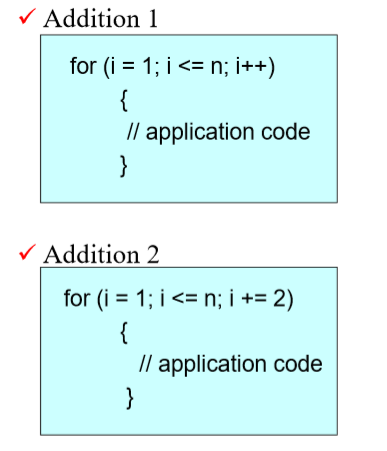
첫번째 사진의 시간복잡도는, n개의 data가 들어왔을 때 for문에서 n번 반복하므로 T(n)=n
두번째 사진의 시간복잡도는, i+=2 이므로 T(n)=n/2

이처럼 data n개에 대한 T(n)들이 n 혹은 n/2 일 경우 n에 대한 1차방정식이다. n이 증가할 때 시간복잡도 역시 증가하되 선형적으로 증가한다.

2.Logarithmic Loops

data n개에 비하여 1,2,4,8,16과 같이 제곱으로 증가한다. 이는 비 선형적으로 i가 증가하여 위의 예와 비교하여 I가 n까지 도달하는 횟수가 더 적으며 그만큼 연산의 횟수가 더 적음을 의미한다.
시간 복잡도는 T(n)=log(n) (밑은 2) 이다.

3. Nested Loops

T(n)=n^2 이다.
입력데이터가 증가함에 따라 연산 횟수의 증가 값이 아주 높다. 그래서 많은 데이터를 처리할 때 바람직하지 못한 알고리즘이다. 알고리즘 문제를 풀때, 시간초과가 뜨는 경우 이런 유형의 시간복잡도를 가지는 함수가 있는지 확인해 봐야 한다.

즉, 공간복잡도는 메모리 사용량에 대한 분석 결과이고 시간복잡도는 속도에 대한 분석 결과이다.

점근 표기법

빅오(big 'oh)

• 모든 n, n>=n0에 대해 f(n) <= cg(n) 인 조건을 만족시키는 두 양의 상수 c와 n0가 존재하면 f(n)=O(g(n))

오메가

• 모든 n, n>=n0에 대해 f(n) >= cg(n)을 만족시키는 두 양의 상수 c와 n0가 존재하면 f(n)=W(g(n))

세타

• 모든 n, n≥n0에 대해 c1g(n)≤ f(n) ≤ c2g(n)을 만족시키는 세 양 의 상수 c1, c2와 n0가 존재하면, f(n) = Q(g(n))