1. 트리란?
트리는 노드로 이루어진 자료구조.
1. 트리는 하나의 루트 노드를 갖는다
2. 루트 노드는 0개 이상의 자식 노드를 갖고있다.
3. 그 자식 노드 또한 0개 이상의 자식 노드를 갖고 있고, 이는 반복적으로 정의된다.
노드(node)들과 노드들을 연결하는 간선(edgd)들로 구성되어있다.
- 트리에는 싸이클(cycle)이 존재할 수 없다.
- 노드들은 특정 순서로 나열 될 수도 있고 그럴 수 없을 수도 있다
- 각 노드는 부모 노드로의 연결이 있을 수도 있고 없을 수도 있다.
- 각 노드는 어떤 자료형으로도 표현 가능하다.
struct Node{
char name[];
struct Node* children;
}트리는 그래프의 한 종류이다.
- 사이클(cycle)이 없는 하나의 연결 그래프(Connected Graph)
- 또는 DAG(Directed Acyclic Graph, 방향성이 있는 비순환 그래프)의 한 종류 이다.
* loop나 circuit이 없다. 당연히 self-loop도 없다- 즉, 사이클이 없다.
- 노드가 N인 트리는 항상 N-1개의 간선을 가진다.
* 즉, 간선은 항상 (Vertex의 개수 -1) 만큼을 가진다. - 루트에서 어떤 노드로 가는 경로는 유일하다.
* 임의의 두 노드간의 경로도 유일하다. 즉, 두개의 정점 사이에는 반드시 1개의 경로만을 가진다. - 한개의 루트 노드만이 존재하며, 모든 자식 노드는 한개의 부모 노드만을 가진다.
* 부모- 자식 관계이므로 흐름은 top-bottom 아니면 bottom-top 으로 이루어진다. - 순회는 전위, 후위, 중위로 이루어지고 이 3가지 모드 DFS/BFS 안에 있다.
- 트리는 이진트리, 이진 탐색트리, 균형트리(AVL트리, red-black 트리), 이진 힙(최대 힙, 최소 힙)등이 있다.
비선형 구조 이다. 비선형 구조는 선형구조와는 다르게 데이터가 계층적(혹은 망)으로 구성되어 있다. 즉 트리는 계층 모델이다. ex) 디렉터리 구조, 조직도
2.트리(Tree)와 관련된 용어
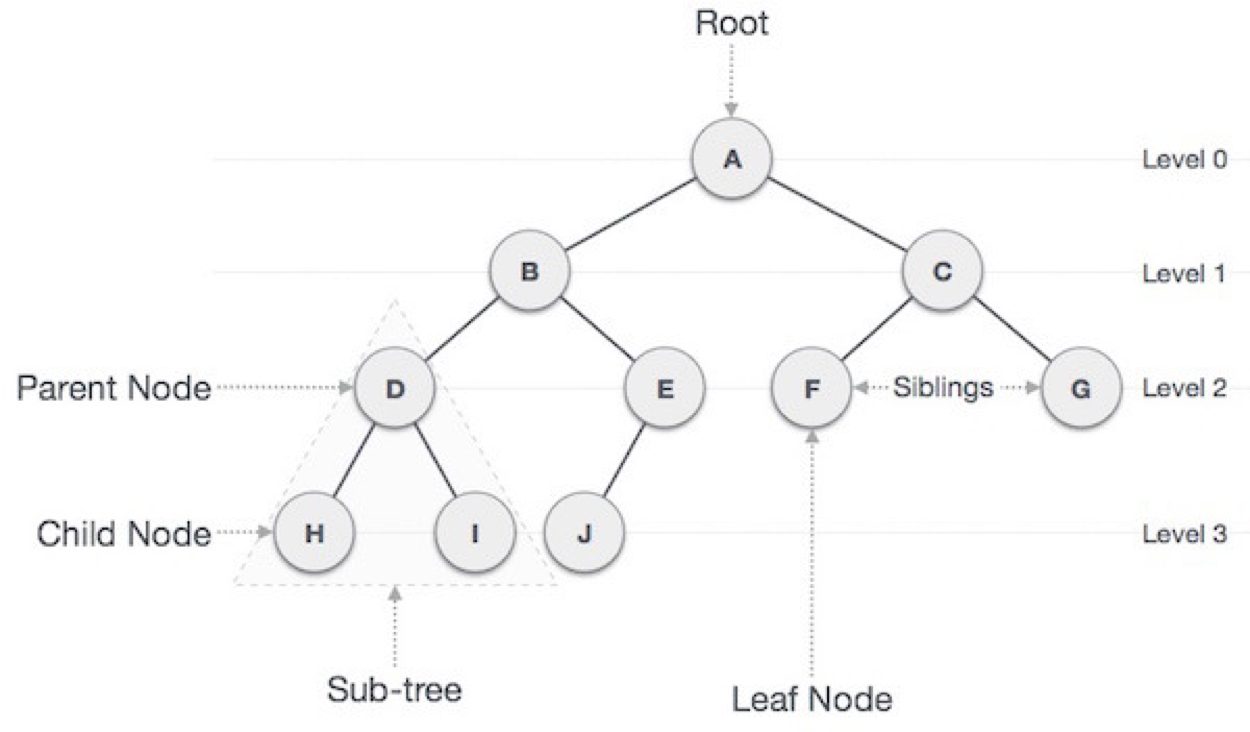
- 루트 노트(root node): 부모가 없는 노드, 트리는 하나의 루트 노드만을 가진다.
- 단말 노드(leaf node): 자식이 없는 노드(차수가 0인 노드), '말단 노드' 또는 '잎 노드'라고도 부른다.
- 내부(internal) 노드 : 단말노드가 아닌 노드.
- 간선(edge): 노드를 연결하는 선(link, branch 라고도 부름)
- 형제(sibling): 같은 부모를 가지는 노드
- 노드의 크기(size): 자신을 포함한 모든 자손 노드의 개수
- 노드의 깊이(depth): 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
- 노드의 레벨(level): 트리의 특정 깊이를 가지는 노드의 집합
- 노드의 차수(degree): 노드의 서브트리 수
- 트리의 차수(degree of tree): 트리의 최대 차수
- 트리의 높이(깊이)(height): 루트 노드에서 가장 깊숙이 있는 노드의 깊이, max{노드레벨}
3. 트리(Tree)의 종류
이진트리(binary tree)
이진트리란?
비어있거나, 루트와 왼쪽 서브트리, 오른쪽 서브트리라고 불리는 두개의 서로소의 이진트리로 구성되어 있는 노드들의 유한 집합.
각 노드가 최대 2개의 child를 갖는다. 모든 트리가 이진트리는 아니다.
- 이진트리와 일반 트리의 차이점
* 트리에서는 어느 노드의 child를 순서로 구분한다.- 이진트리에서는 child가 한개인 경우도 left child 인가 right child 인가에 따라 다른 이진트리로 간주된다.
레벨 i에서의 최대 노드 수 : 2^(i-1) (i>=1)
깊이가 k인 이진트리가 가질 수 있는 최대 노드 수 : 2^k-1 (k>=1)
리프노드수 = 차수가 2인 노드 수 + 1포화 이진트리(full binary tree)
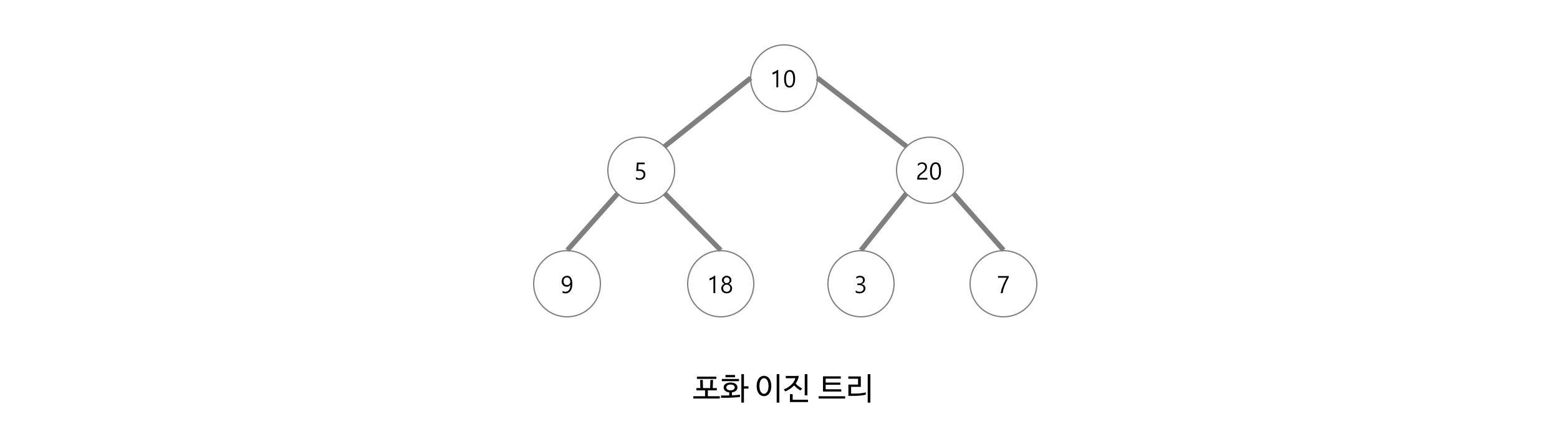
- 깊이가 k이고, 노드 수가 2^k-1(k>=0) 인 이진트리
- 노드 번호 1,...,2^k-1까지 순차적인 부여 가능
- 모든 말단 노드는 같은 높이에 있어야 하며, 마지막 단계에서 노드의 개수가 최대가 되어야 한다.
- 모든 내부 노드가 두개의 자식 노드를 갖는다.
- 모든 말단 노드가 동일한 깊이 또는 레벨을 갖는다.
완전 이진 트리(complete binary tree)
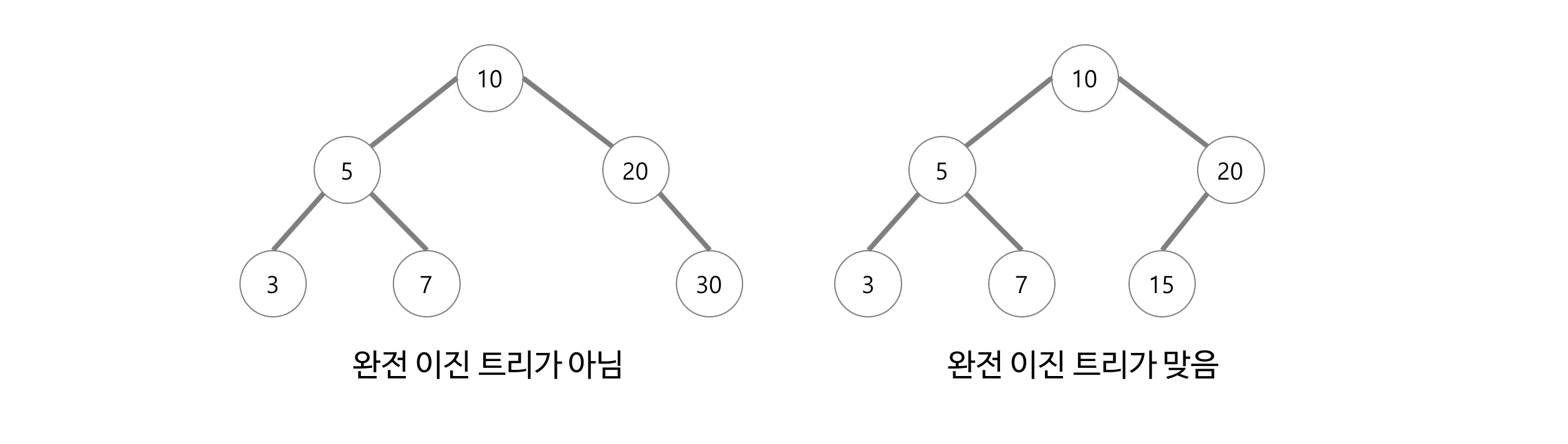
- 깊이가 k이고 노드 수가 n인 이진 트리
- 각 노드들이 깊이가 k인 포화이진 트리 에서 1부터 n까지 번호를 붙인 노드와 1대 1로 일치
- 트리의 모든 높이에서 노드가 꽉 차 있는 이진트리. 즉, 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있어야 한다.
- 마지막 레벨은 꽉 차 있지 않아도 되지만 노드가 왼쪽에서 오른쪽 으로 채워져야 한다.
- 배열을 사용해 효율적으로 표현 가능
이진 탐색 트리(Binary Search Tree, BST)
- 모든 노드가 아래와 같은 특정 순서를 따르는 속성이 있는 이진 트리
* 모든 왼쪽 자식들 <= N < 모든 오른쪽 자식들 (모든 노드 N에 대해서 반드시 true) - 왼쪽, 오른쪽 서브트리도 BST
- 사전(dictionary) : pair<키, 원소>의 집합
* 모든 원소는 서로 상이한 키를 갖는다.
균형 트리, 비균형 트리
- 균형 트리
* O(log N) 시간에 insert와 find를 할 수 있을 정도로 균형이 잘 잡혀 있는 경우- 레드-블랙 트리, AVL 트리
이진 힙(최소힙과 최대힙)
-
최소 힙 (Min Heap)
트리의 마지막 단계에서 오른쪽 부분을 뺀 나머지 부분이 가득 채워져 있는 완전 이진트리 이며, 각 노드의 원소가 자식들의 원소보다 작다.
즉, key(부모 노드) <= key(자식 노드)인 완전 이진 트리
가장 큰 값은 루트 노드이다.
N개가 힙에 들어가 있으면 높이는 log(N_ 이다. -
최대 힙(Max Heap)
* 원소가 내림차순으로 정렬되어 있다는 점에서만 최소힙과 다르다.- 각 노드의 원소가 자식들의 원소보다 크다
-
트라이(Trei) (접두사 트리(prefix tree) 라고도 부른다)
* n-차 트리의 변종- 각 노드에 문자를 저장하는 자료구조
- 따라서 트리를 아래쪽으로 순회하면 단어 하나가 나온다.
- 접두사를 빠르게 찾아보기 위한 흔한 방식으로, 모든 언어를 트라이에 저장해 놓는 방식이 있다.
- 유효한 단어 집합을 이용하는 많은 문제들은 트라이를 통해 최적화할 수 있다.
4.트리(tree)의 구현 방법
기본적으로 트리는 그래프의 한 종류이므로 그래프의 구현방법(인접 리스트 또는 인접 배열)로 구현할 수 있다.
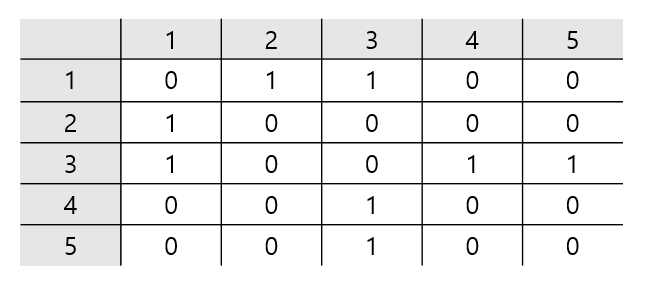
인접 행렬 이용 (adjacency matrix)
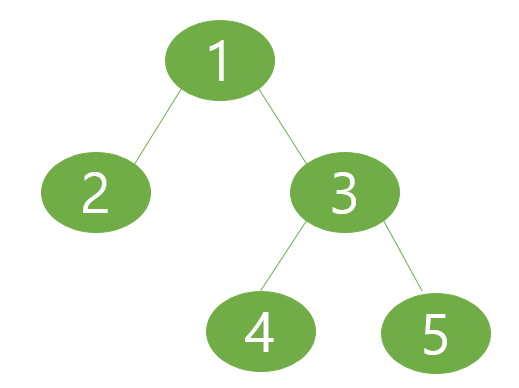
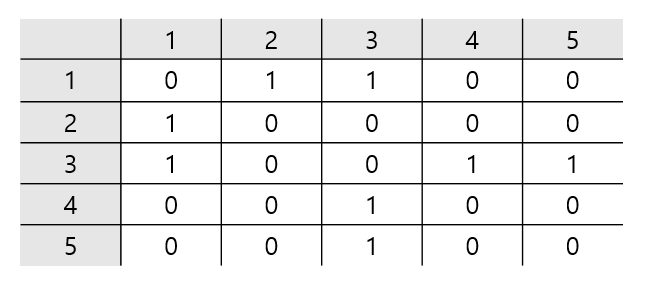
인접 배열 이용
- 1차원 배열에 자신의 부모 노드만 저장하는 방법
<보조정리>
-n개의 노드를 가진 완전 이진 트리
1. parent(i) : i/2 (if i!=1)
2. leftChild(i) : 2i (if 2i<=n)
왼쪽 자식 없음 (if 2i > n)
3. rightChild(i) : 2i+1 (if 2i+1<=n)
오른쪽 자식 없음 (if 2i+1 > n)
- 트리는 부모 노드를 0개 또는 1개를 가지기 때문
- 부모 노드를 0개 : 루트 노드
- 이진 트리의 경우, 2차원 배열에 자식 노드를 저장하는 방법.
- 이진트리는 각 노드가 최대 2개의 자식을 갖는 트리이기 때문.
* ex) A[i][0]:왼쪽 자식 노드, A[i][1]: 오른쪽 자식 노드
인접 리스트 이용
5. 트리(Tree) 의 순회
트리 순회(tree traversal)
-트리에 있는 모든 노드를 한 번씩만 방문
1. 중위 순회(Inorder Traversal)
- 왼쪽 자식 방문->루트 방문->오른쪽 자식 방문 (LVR)
template <class T>
void Tree<T>::Inorder(TreeNode<T> *currentNode){
if(currentNode){
Inorder(currentNode->leftChild);
Visit(currentNode);
Inorder(currentNode->rightChild);
}
}(non-recursive version)
void Tree<T>::NonrecInorder(){
Stack<TreeNode<T>*> s;
TreeNode<T> * currentNode = root;
while(1){
while(currentNode){ //Move down leftChild fields
s.Push(currentNode);
currentNode = currentNode->leftChild;
}
if(s.IsEmpty()) return;
currentNode = s.Top; s.Pop();
Visit(currentNode);
currentNode = currentNode->rightChild;
}
}- 전위 순회(Preorder Traversal)
- 루트 방문 -> 왼쪽 자식 방문 -> 오른쪽 자식 방문 (VLR)
template<class T>
void Tree<T>::Preorder(TreeNode<T> *currentNode){
if(currentNode){
visit(currentNode);
Preorder(currentNode->leftChild);
Preoreder(currentNode->rightChild);
}
}- 후위 순회(Postorder Traversal)
- 왼쪽 자식 방문 -> 오른쪽 자식 방문 -> 루트 방문(LRV)
template<class T>
void Tree<T>::Postorder(TreeNode<T> *currentNode){
if(currentNode){
Postorder(currentNode->leftChild);
Postoreder(currentNode->rightChild);
visit(currentNode);
}
}그래프와 트리의 차이