그래프

그래프는 정점과 간선으로 구성된 비선형 데이터 구조입니다. 정점은 노드라고도 불리며 간선은 그래프에서 두 노드를 연결하는 선이나 호로 표시됩니다. 공식적으로 그래프는 정점(V)의 집합과 간선(E)의 집합으로 구성됩니다. 그래프는 G(V, E)로 표시됩니다.

그래프 데이터 구조는 오브젝트나 엔티티 사이의 복잡한 관계를 분석하고 표현하는데 강력한 도구입니다. 그래프는 소셜 네트워크 분석, 추천 시스템, 그리고 컴퓨터 네트워크와 같은 분야에서 특히 유용합니다. 스포츠 데이터 과학의 영역에서, 그래프 데이터 구조는 팀의 능력과 필드 위의 플레이어 상호작용 역학을 이해하고 분석하는데 사용됩니다.

축구 경기를 연결망(web of connection)으로 상상해 보세요. 여기 플레이어들은 노드가 되고 필드에서 그들의 상호작용은 간선이 됩니다. 이러한 연결망은 정확히 그래프 데이터 구조를 표현합니다. 그리고 이는 스포츠에서 팀의 능력과 선수의 역학에 대한 통찰력을 얻는 열쇠가 됩니다.

그래프의 구성

정점(Vertice)

• 정점은 그래프의 기본 단위입니다. 때때로, 정점(Vertice)은 정점(Vertex)이나 노드(nodes)로 알려져 있습니다. 모든 노드/정점은 라벨을 붙이거나 붙이지 않을 수 있습니다.

간선(Edges)

• 간선은 그래프에서 두 노드를 연결하는데 사용됩니다. direted graph에서 두 노드 쌍을 정렬할 수 있습니다. 간선은 두 노드를 어떠한 방법으로 연결할 수 잇습니다. 여기에는 규칙이 없습니다. 때떄로, 간선들은 호라고 알려져 있습니다. 모든 간선은 라벨을 붙이거나 붙이지 않을 수 있습니다.

그래프의 종류

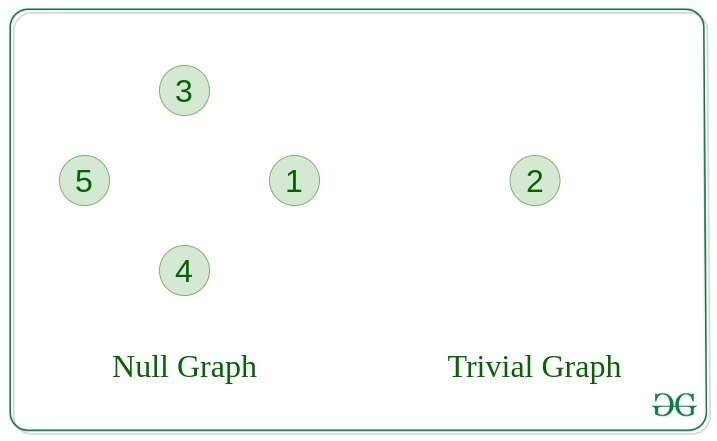
Null 그래프

• 만약에 그래프에 간선이 하나도 없다면 이 그래프는 Null 그래프라고 불립니다.

Trivial 그래프

• 단 하나의 정점을 가지는 그래프를 가진 그래프를 말합니다. 가장 작은 그래프이기도 합니다.
  

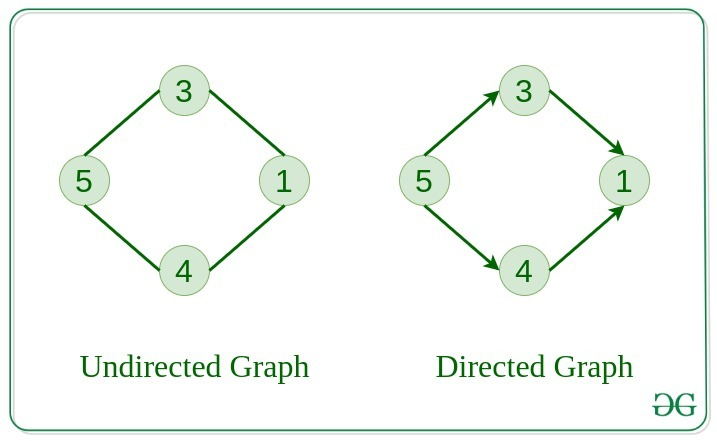
Undirected 그래프

• 그래프의 간선에 방향이 정해지지 않은 그래프입니다. 모든 간선에 대해서 노드들은 순서가 정해지지 않은 쌍으로 이루어져 있습니다.

Directed 그래프

• 그래프의 간선에 방향이 정해진 그래프입니다. 모든 간선에 있어서 노드들은 순서쌍으로 이루어져 있습니다.
  

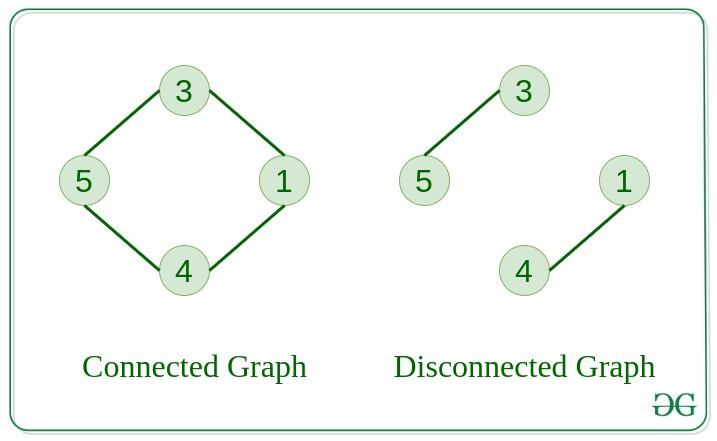
Connected 그래프

• 그래프의 한 노드로부터 모든 다른 노드들을 방문할 수 있다면, 이를 connected 그래프라고 합니다.

Disconnected 그래프

• 그래프의 최소한 한 노드로부터 도달할 수 없는 노드가 존재한다면, 이를 disconnected 그래프라고 합니다.
  

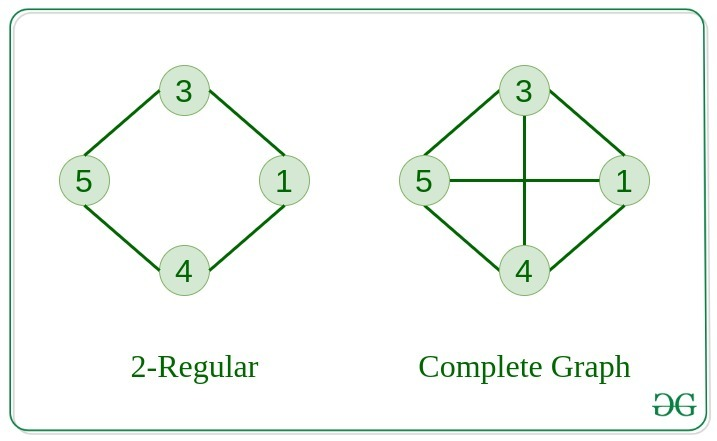
Regular 그래프

• 그래프의 모든 정점의 차수에 대해서, K로 동일하다면, 이를 K-Regular 그래프라고 합니다.

Complete 그래프

• 그래프의 각 노드에 대해서, 다른 모든 노드에 대해 간선이 존재한다면, 이를 Complete 그래프라고 합니다.
  

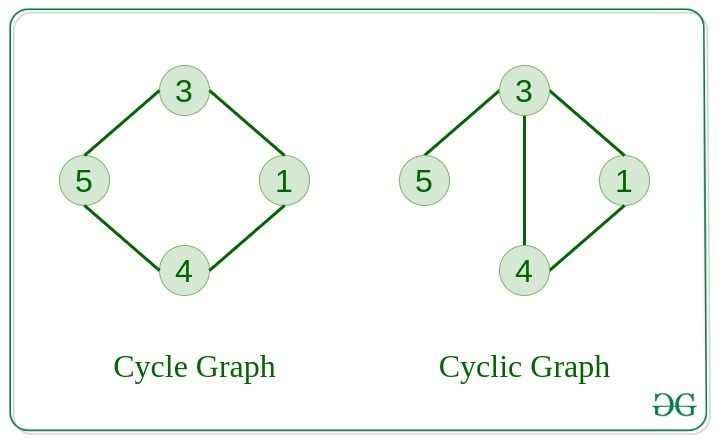
Cycle 그래프

• 그래프가 그 자체로 순환하고, 각 정점의 차수가 2인 그래프를 Cycle 그래프라고 합니다.

Cyclic 그래프

• 그래프에서 최소한 하나의 순환이 존재한다면, 이는 Cyclic 그래프라고 합니다.
  

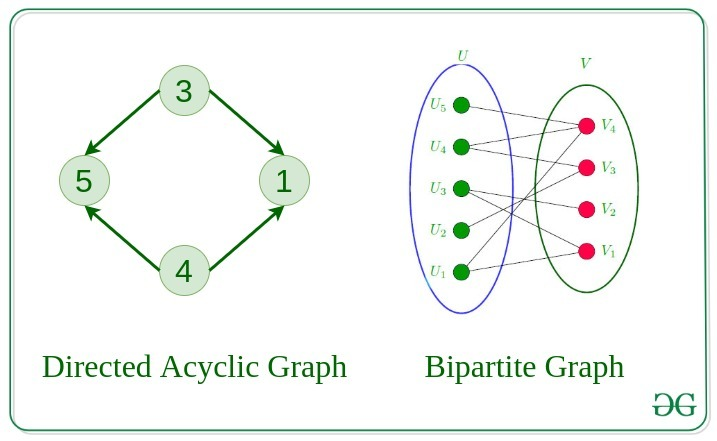
Directed Acyclic 그래프

• 어떠한 순환도 존재하지 않은 Directed 그래프를 Directed Acyclic 그래프라고 합니다.

Bipartite 그래프

• 그래프의 정점이 두 정점 집합으로 나눠지고 각 집합의 정점 사이에 간선이 존재하지 않는 그래프를 Bipartite 그래프라고 합니다.
  

Weighted 그래프

• 그래프의 각 간선들에 가중치가 명시된 그래프를 Weighted 그래프라고 합니다.