https://www.acmicpc.net/problem/1008

요즈음 자료구조를 공부한다고 백준 리뷰는 쉬운 것만 풀면서 최대한 건너뛰려고 했으나 이 문제만큼은 한번 짚고 넘어가야할 것 같았다.
이는 문제 자체보다 문제를 풀며 고민하게 된 실수의 나눗셈에 대한 내용이므로 C언어 공부 시리즈에 추가한다.
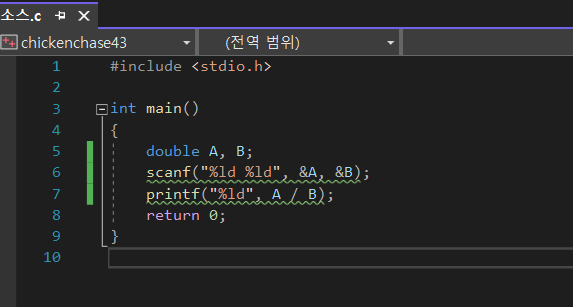
처음에 lf를 써야 하는데 ld를 쓴 실수한 코드인데
A = 1, B = 3을 대입하니 -2가 출력되었다.
둘다 정수로 입력되었다고 해도 분명 0이 출력되어야 하는데 말이다.
그 이유를 알아보자.

입력 전 A,B의 값이 저러한데
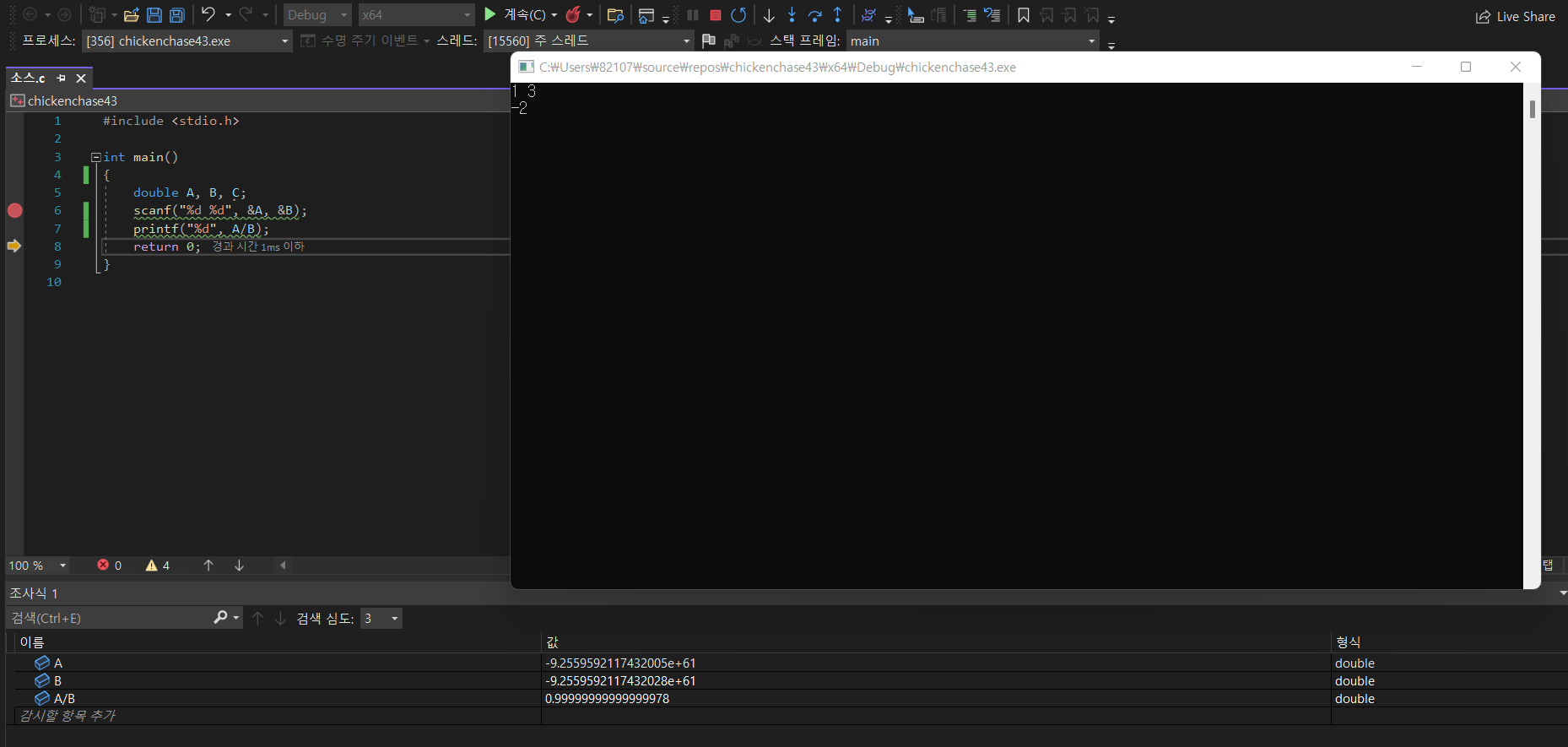
입력 후에도 A,B의 값이 바뀌지 않았고
출력도 A/B와 전혀 상관없는 값이 출력됐다.
즉, scanf로 정수포멧으로 받아오면 실수형 변수는 입력을 받지 못하고
정수형 포멧으로 출력해도 마찬가지로 전혀 엉뚱한 값을 출력한다.
그리고 이 문제를
#include <stdio.h>
int main()
{
double A, B;
scanf("%lf %lf", &A, &B);
printf("%lf", A / B);
return 0;
}이렇게 제출하면 틀리게 되는데 이는 소수점 6자리까지만 반올림하여 출력하기 때문이다.
그래서 이를 방지하려면 출력포멧을 %.11f, %.15f 등으로 해주어야 하는데
과연 float, double 포멧은 몇자리까지 정확하게 출력할 수 있을까?
그리고 소수 부분은 이진수로 어떻게 처리할까?
일단 float은 4바이트, double은 8바이트이므로
각각 32비트, 64비트 즉, 2진수 32자리, 64자리로 표현가능하다.
그러면 소수 부분을 이진수로 어떻게 처리하는지 알게 되면 이 문제는 해결할 수 있다.
https://pang2h.tistory.com/293
이 밑의 내용은 위의 티스토리 블로그의 주소를 인용하여 작성하였음을 미리 알립니다.
우선 33.75를 이진수로 바꿔보자.
정수 부분은 십진수를 이진수로 바꾸는 방식을 그대로 취하여 100001이 된다.
소수 부분은 우선 십진수를 예시로 들어보면
0.1234는 곱하기 10을 하면 1.234 이의 정수 부분을 10으로 나눈 나머지는 1
같은 방식으로 2,3,4가 도출되므로 이 소수는 0.1234로 표기된다.
즉 0.75는 0.75 2 = 1.5
0.5 2 = 1 이므로
33.75 = 100001.11이다.
이는 다시 1.0000111 * 2^5이다.
이를 메모리에 넣어야 하는데 자료형들의 구조는 다음처럼 되어 있다.
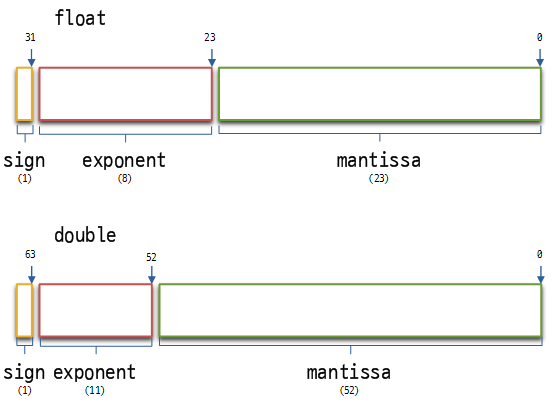
이 때 exponent는 지수부, mantissa는 가수부라 하는데
가수부에는 위의 10000111이 상위 7개의 비트가 들어가고 진수부에는 2^5의 5가 들어가는데 이 때, 진수부의 지수는 음수일수도 있다.
즉, 진수부는 127이면 0으로 취급하여 128 ~ 255 는 1 ~ 128
0 ~ 126은 -127 ~ -1 로 취급한다.
즉 여기서 5는 127 + 5인 132로 10000100이 지수부에 기록된다.
그럼 이 문제에서는 소수가 어디까지 정확할 수 있는지 보자.
이 문제에서 정수부는 최대 9이므로 최대 1001로 비트를 네자리 차지한다.
그러면 double형에서 나머지 48자리는 소수부분이 무조건 차지하는데
이는 1/2의 48제곱까지 표현가능하다. (햇갈리면 10진수로 생각하면 편하다)
이 때 2의 48제곱이 281,474,976,710,656 이므로 10의 14제곱 분의 1 즉, 소수점 14자리까지는 정확히 표현가능함을 알 수 있다.
따라서 이 문제의 범위에서는 .14f까지 정확하게 출력이 가능하다.
