1. 미래도시

• 첫째 줄에 노드 개수 N과 경로 개수 M이 공백으로 구분되어 입력됨.(1<= N,M <= 100)
• 둘째 줄부터 M+1 번째 줄에는 연결된 두 노드의 번호가 공백으로 구분되어 입력됨.
  • 연결된 두 노드는 양방향으로 이동가능하며 거리는 모두 1이다.
• M+2번째 줄에 X와 K가 공백으로 구분되어 입력됨(1<=K,X<=100)

1번 노드 > K번 노드 > X번 노드에 도착하는 최단 거리 구하기
(X번 노드에 도착할 수 없다면 -1을 출력)

1.1 내 답안

• 노드 개수 범위가 크지 않아서 플로이드 워셜 알고리즘 씀.
• 실수 : INF = 1e9는 실수로 정의됨. -> INF = int(1e9) 정수로 정의해야함.

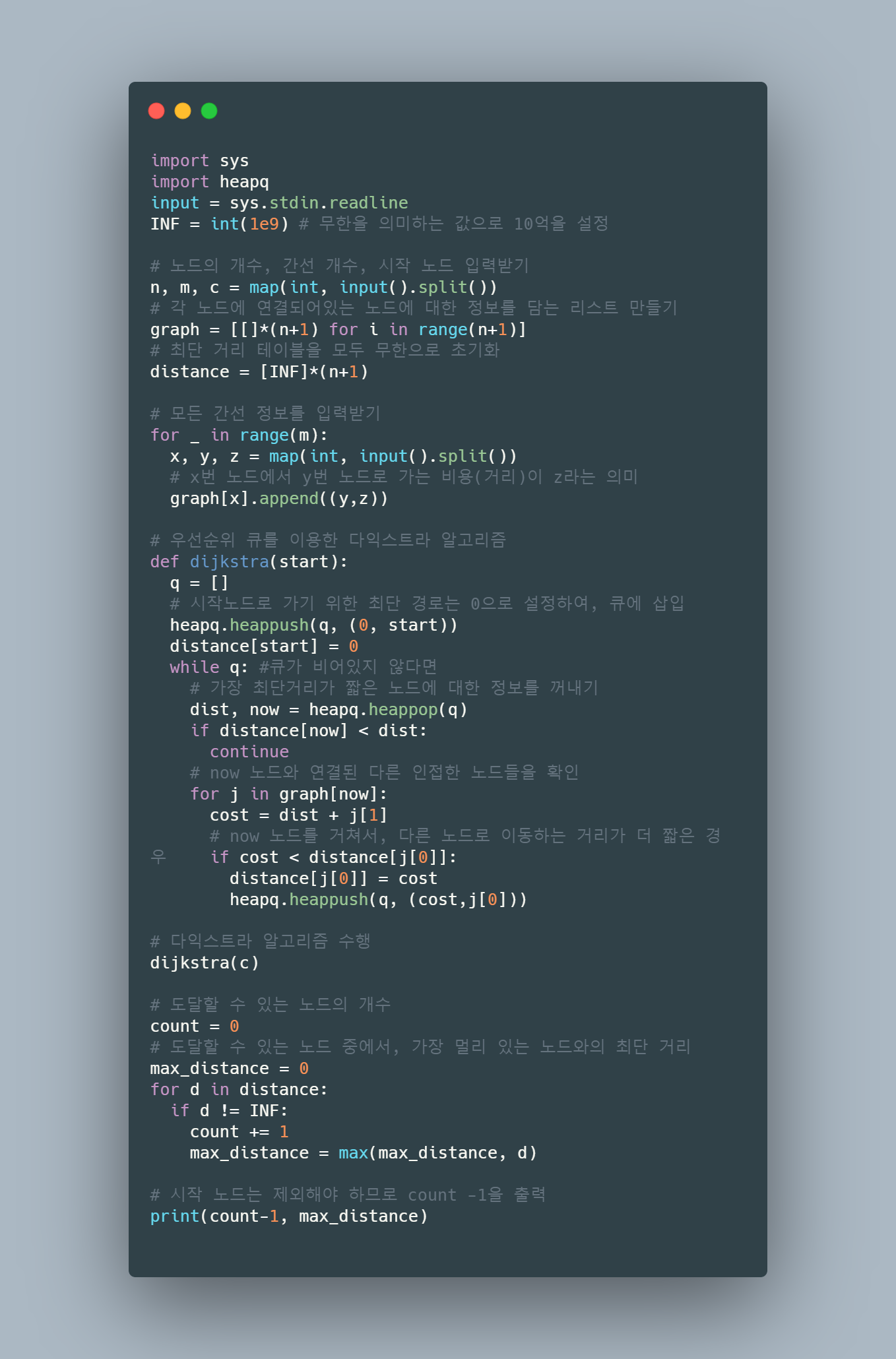
import sys
input = sys.stdin.readline

n, m  = map(int, input().split())
INF = 1e9
graph = [[INF]*(n+1) for i in range(n+1)]


for a in range(1,n+1):
  for b in range(1,n+1):
    if a==b:
      graph[a][b] = 0

for _ in range(m):
  a, b = map(int, input().split())
  graph[a][b] = 1
  graph[b][a] = 1
x, k = map(int, input().split())

# 1번 회사 -> K번 회사 최단거리 +
# K번 회사 -> X번 회사 최단거리

for m in range(1,n+1):
  for a in range(1, n+1):
    for b in range(1, n+1):
      graph[a][b] = min(graph[a][b] , graph[a][m]+graph[m][b])

if graph[1][k]==INF or graph[k][x] == INF:
  print(-1)
else:
  print(graph[1][k]+graph[k][x])

1.2 책 답안

• 코드를 이미지로 변환하는 사이트 이용해봄~
• 📌사이트 : https://carbon.now.sh/

2. 전보

• 한 도시에서 다른 도시까지 전보를 보내는 시간에 대한 문제인데 편의상 최단거리 문제로 단순화하여 기록했음.
• 첫째 줄에 노드개수 N, 간선개수 M, 시작 노드 C가 주어짐.(1<=N<=30,000, 1<=M<=200,000, 1<=C<=N)
• 둘째 줄부터 M+1번째 줄까지 모든 간선 정보(X,Y,Z)가 입력됨.
• (X,Y,Z) : X노드에서 Y노드까지 이어지는 간선이 있으며 거리는 Z라는 정보 (1<=X,Y<=N, 1<=Z<=1,000)

출력) 시작 노드에서 출발하여 도달할 수 있는 노드 개수와 최대 시간

2.1 내 답안

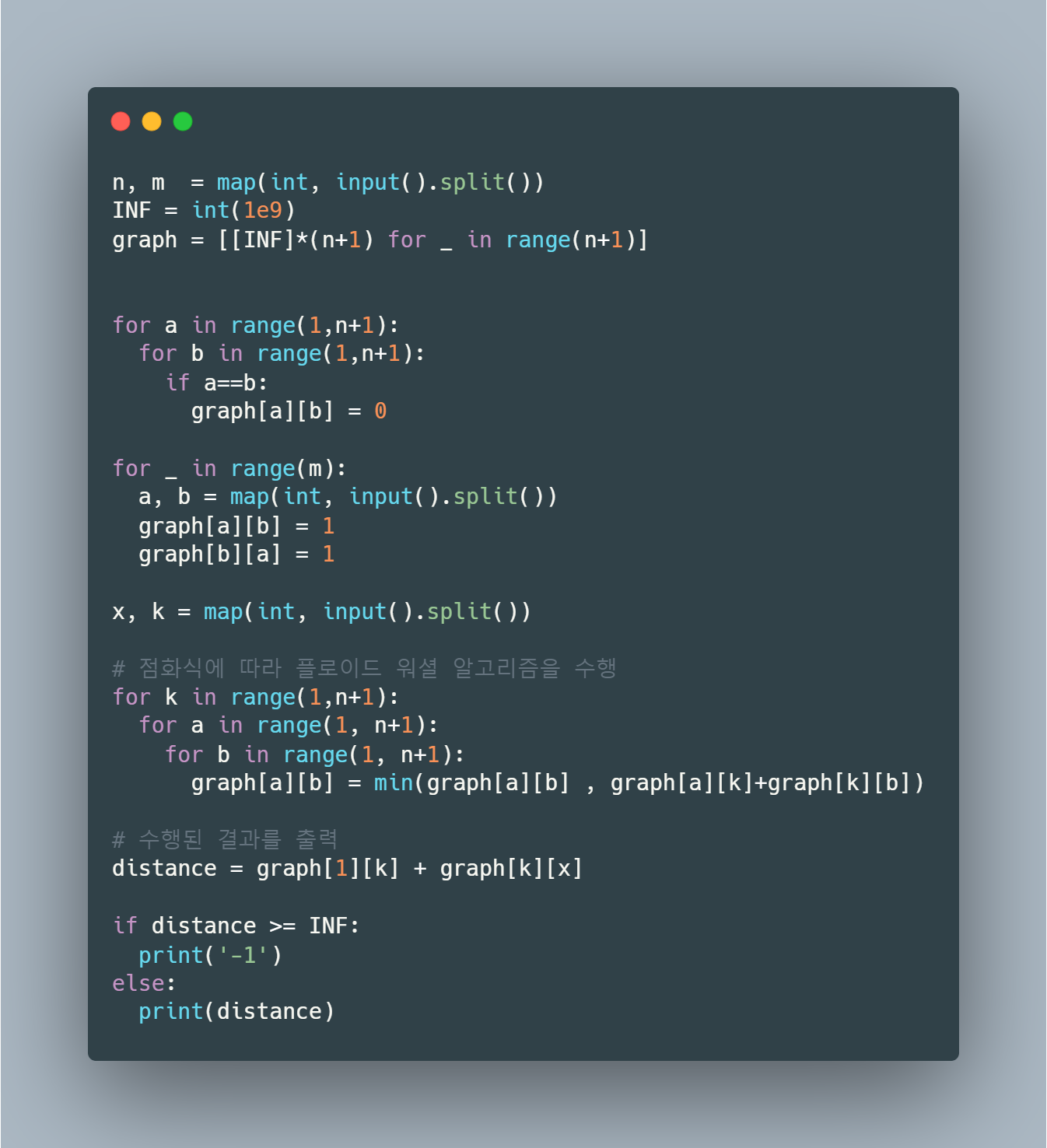
import sys
import heapq
input = sys.stdin.readline

n, m, c = map(int, input().split())
INF = int(1e9)
graph = [[]*(n+1) for i in range(n+1)]
distance = [INF]*(n+1)

for _ in range(m):
  x, y, z = map(int, input().split())
  graph[x].append((y,z))

def dijkstra(start):
  q = []
  heapq.heappush(q, (0, start))
  distance[start] = 0
  while q:
    dist, now = heapq.heappop(q)
    if distance[now] < dist:
      continue
    for j in graph[now]:
      cost = dist + j[1]
      if cost < distance[j[0]]:
        distance[j[0]] = cost
        heapq.heappush(q, (cost,j[0]))
dijkstra(c)
result = [x for x in distance if x != INF and x != 0]

print(len(result),max(result))

2.2 책 답안