알고리즘
최대, 최소가 필요한 연산에대해서는 항상 heap을 생각해주자.
heap을 생각할 때는, 복잡하게 생각할 것 없이 부모와 자식의 대소관계에대해서만 생각해주면 된다.
리스트를 이용해서 구현할 경우에는
idx//2 -> 부모
idx2,idx2+1 -> 자식
이다.
heap에서 원소의 추가 및 삭제의 시간 복잡도는 O(logN)이다. 그리고 삭제는 heap의 root node를 삭제하는 과정이라는 것을 꼭 알아야겠다.
python 에서는 import heapq로 힙을 구현해놓은 라이브러리를 가져다가 쓸 수 있다.
이 heapq라이브러리는 최소힙으로 작동하는데, heapq라이브러리를 최대 힙으로 사용하고싶으면, heap에 data를 집어넣을 때, -를 붙여서 넣어주면된다.
DFS, BFS
stack을 사용하고 queue를 사용하는 방식으로 구현이 나뉜다.
끝까지 내려가봐야하는 경우에는 DFS를 사용하고, 그 이외에 최단경로 및 모든 경우의 수를 따져봐야하는 경우에는 BFS가 좋을 것 같다.
그리고 특히 DFS, BFS로 푸는 문제들 중에서 2차원 공간에대한 움직임을 고려하는 경우가 많다.
이 경우에는 각 축의 방향으로의 방향 벡터를 만들어놓고, 조건에 맞는 이동 방향을 계산 후 그 방향으로 이동하게 해주면된다.
DP
예전에 그런 말을 들은 적이 있다.
"DP 문제는 점화식만 만들어내면, 다 푼 문제다."
주어진 상황들을 보면서 고등학교 때 배웠던 수열들의 실생활 예제를 푼다는 생각으로 푸니까 머리가 그쪽으로 잘 돌아가는 것 같다. 꼭 바로 직전의 값들만을 이용하는 것이 아니라, 그냥 지금 단계를 해결하기위한 부분문제들의 값들을 메모해놨다가 필요할 때, 보고 쓰는 느낌으로 이해했더니 감이 잘 왔다.
추가적으로 배열에서 항상 index를 헷갈렸는데, 일반 좌표평면에서 x축이 열이고, y축이 행이라 생각해야지 안꼬인다.
2차원 배열의 구조를 잘 생각해보자.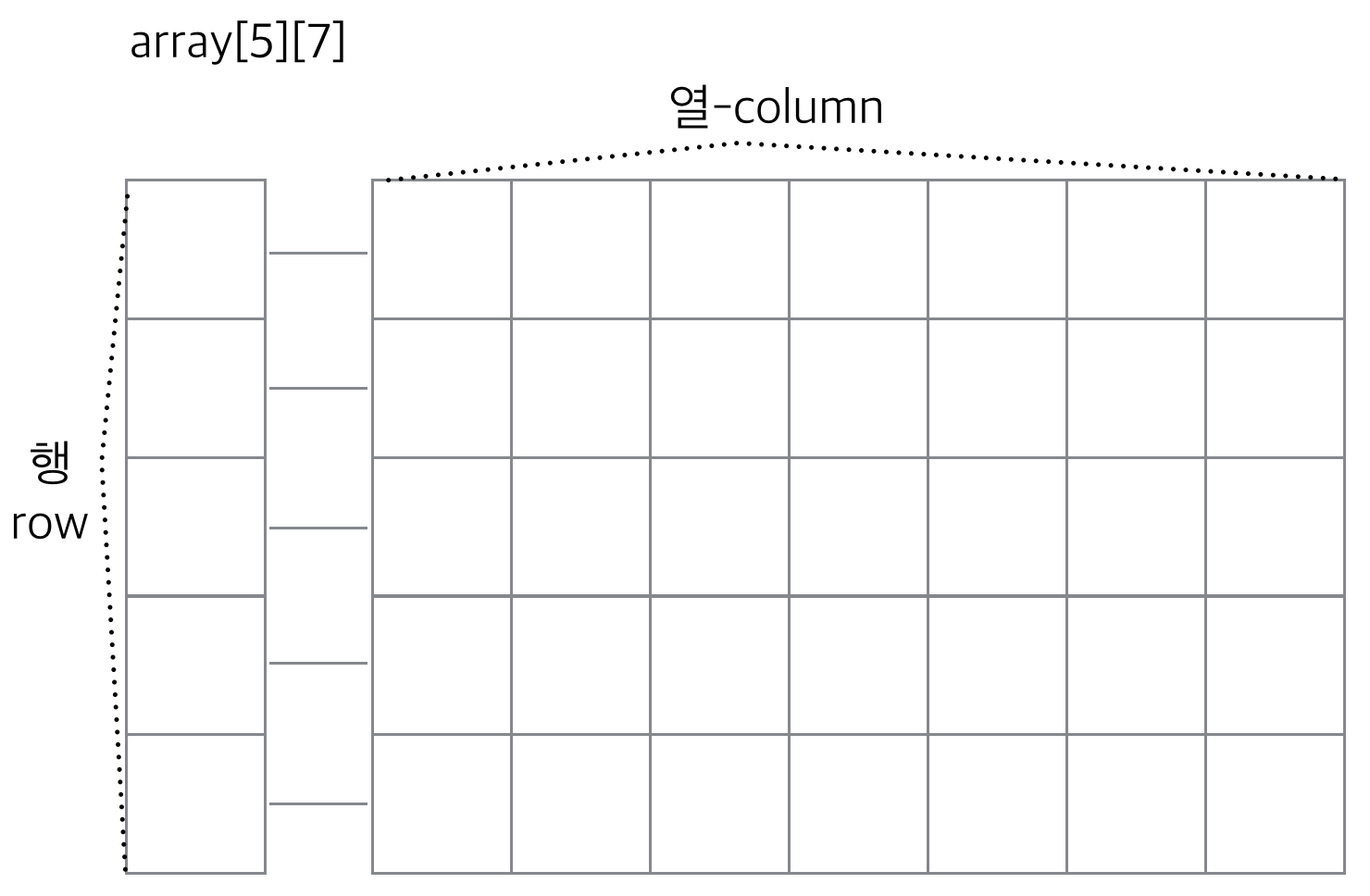
항상 인덱스 행열 숫자를 바꿔서 풀다가 삽질해서 멘붕왔었으니까 침착하게 구조부터 파악하고 머리에서 정리를 끝내고서 코드화를 들어가자 반드시!
추가로 변수명을 row와 col, r과 c 처럼 두면 코드를 짜면서 덜 헷갈린다.

