문자열에서 패턴 찾기
위의 그림과 같이 문서에서 찾고자하는 단어가 있을 때, 찾기 기능을 안 써본 사람은 없을 것입니다.
이 때 문서(이하 문자열)에서 찾고자하는 단어(이하 패턴)를 찾을 때 아래와 같이 하나하나 찾아보는 방식을 떠올리기 쉽습니다.
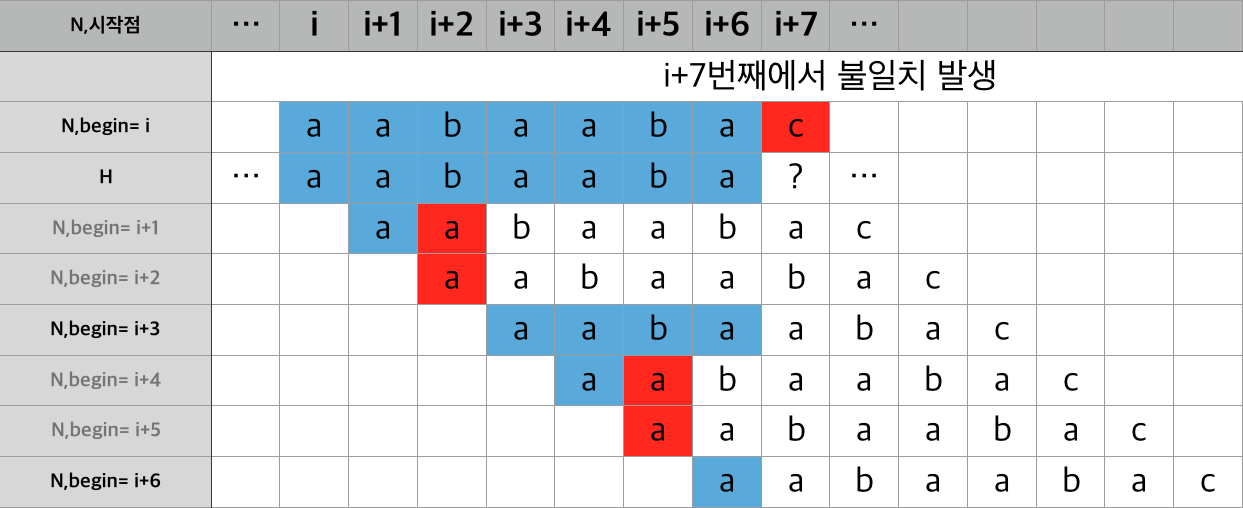
위의 그림에서 빨간색으로 칠해진 부분은 불일치가 발생한 부분입니다.
불일치가 발생하면 해당 시작 위치는 정답을 위한 시작위치가 될 수 없습니다.
위의 그림에서처럼 하나하나 찾다보면 전체 문자열의 길이를 N, 패턴의 길이를 M이라하면 O(NM)의 시간만큼 소요될 것입니다.
이런 문자열에서 패턴을 찾는 것을 O(N+M)까지 줄여줄 수 있는게 바로 KMP 알고리즘입니다.
KMP 알고리즘은 무엇인가
KMP 알고리즘은 문자열 탐색 알고리즘입니다.
주어진 문자에서 찾고자하는 패턴을 찾아내기 위한 과정에서 불필요한 연산을 줄여서 수행시간을 개선한 알고리즘입니다.
KMP 알고리즘에서 주목해야할 점은 보지 않고도 알 수 있는 것입니다.
KMP 알고리즘은 문자열에서 패턴을 탐색하는 과정에서 얻는 정보를 버리지 않고 활용합니다.
그렇다면 어떤 정보를 사용할까요??
문자열을 탐색하다보면 비교과정에서 불일치하는 부분이 발생합니다.
이 때, 불일치가 발생한 텍스트 문자열의 앞 부분에 어떤 문자가 있는지에대한 정보를 사용합니다.
미리 알고 있어서 불일치가 발생한 앞부분 중 비교하지않고도 알 수 있는 부분을 건너뛰어 불필요한 비교를 하지않고 매칭을 수행할 수 있습니다.
KMP 알고리즘에서는 건너뛴 새로운 시작 위치를 접두사와 접미사를 이용해서 결정합니다.
KMP 알고리즘의 구조
- 전처리 과정(부분일치 테이블)
- 문자열 탐색(패턴 포인터를 움직임)
제가 KMP를 처음 접했을 때, 가장 헷갈렸던 것은 부분일치 테이블의 생성 시기와 새로운 탐색위치였습니다.
찾아야하는 패턴은 불변이라는 것만 생각하면 패턴 찾기 전에 미리 부분일치 테이블을 만들어놓은 후에 탐색할 때 사용해도 아무 문제없다는 것을 알 수 있습니다.
이 때, 부분일치 테이블의 값을 정하는 기준은 현재 시작 위치에서 문자열(H)과 패턴(N)을 비교했을 때, 몇 글자나 일치했는가입니다.
이를 확인하기 위해서 접두사와 접미사를 사용하는데, 그 이유는 아래의 그림 한 장으로 설명이 가능합니다.
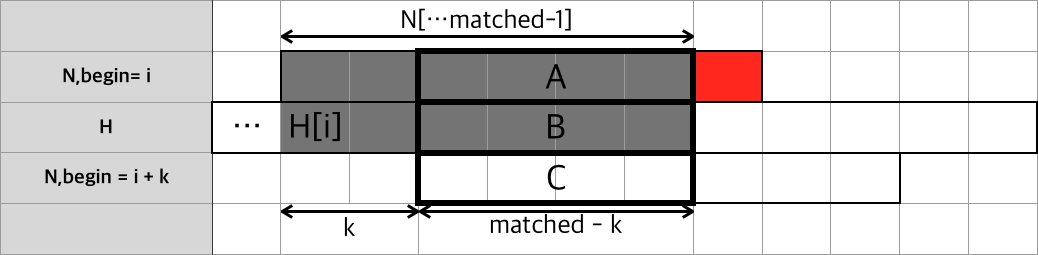
위 그림은 패턴 매칭을 시작한 위치 i에서 H와 N을 맞춰봤을 때, matched 글자가 일치한 후에 그 다음 글자에서 불일치가 발생한 상황입니다.
다음 비교는 불일치가 발생하기 전까지 일치한 패턴의 부분문자열의 접미사와 패턴의 접두사가 일치하는만큼은 안봐도 일치함을 알 수 있습니다.
위의 그림에서 A,B는 직전까지 확인을 진행했던 부분의 접미사이고 C는 접두사입니다.
간단히 말해, 직전까지 확인했던 문자열 중에서 불일치가 발생한 시점으로부터 matched-k 길이의 접미사와 패턴의 시작점부터 matched-k 길이의 접두사가 같다면 접두사 부분은 이미 일치한다는 것이 보장된 상태입니다.
따라서 matched-k길이만큼은 비교하지않고 그 다음부터 패턴이 일치하는지 확인을 진행해도 문제가 없습니다.
이런 특징은 불필요한 비교를 줄여줄 강력한 무기가 됩니다.
그래서 답이 될 수 있는 바로 다음 위치를 찾기 위해서 N의 각 접두사에대해서 접두사도 되고 접미사도 되는 문자열의 최대 길이를 계산해놓는다면, 현재 확인하는 문자열의 포인터는 가만히 놔둔 상태로 패턴의 포인터만 옮겨서 새로운 시작 포인트에서 비교를 진행할 수 있습니다.
이 때, 최대 길이를 계산하는 부분에 사용되는 것이 바로 부분일치 테이블입니다.
부분일치 테이블
매칭이 실패했을 때, 패턴 포인터가 돌아갈 곳을 계산해놓은 테이블로 게임에서 볼 수 있는 세이브 포인트와 비슷한 개념입니다.
일치하는 것이 실패했을 때, 어떻게 해야할지를 알려주는 배열이라는 의미에서 실패 함수라고 부르기도 합니다.
실패함수는 보통 pi[] 배열을 이용해서 표현합니다.
pi[i] = 패턴의 시작부터 i번째 문자로 구성된 부분 문자열의 접두사도 되고 접미사도 되는 문자열의 최대 길이
pi[ ]는 패턴이 어디까지 일치했는지 주어질 때, 다음 시작위치를 어디로 해야할지를 저장하고 있는 배열입니다.
부분 일치했을 때, 다음 시작 위치를 알려주는 특성 때문에 부분일치 테이블이라고 합니다.
부분일치 테이블이 담고있는 정보는 새롭게 탐색을 진행해야하는 패턴 내의 위치입니다. 테이블에는 접두사도 되면서 접미사도 되는 문자열의 최대 길이가 담겨있기 때문에, 이를 이용해 패턴의 시작점부터 그 길이만큼은 비교를 생략할 수 있습니다.
다음은 부분일치 테이블을 만드는 그림입니다.
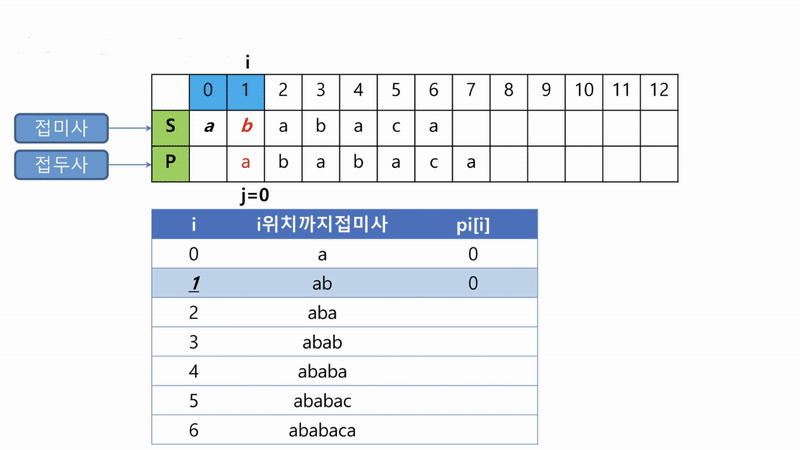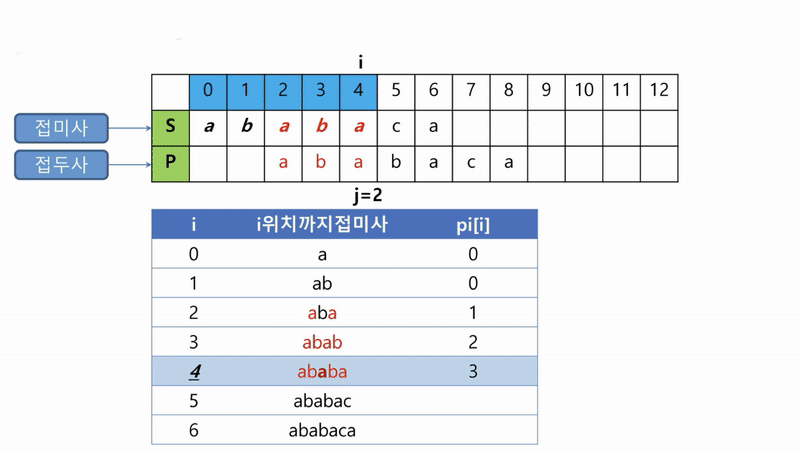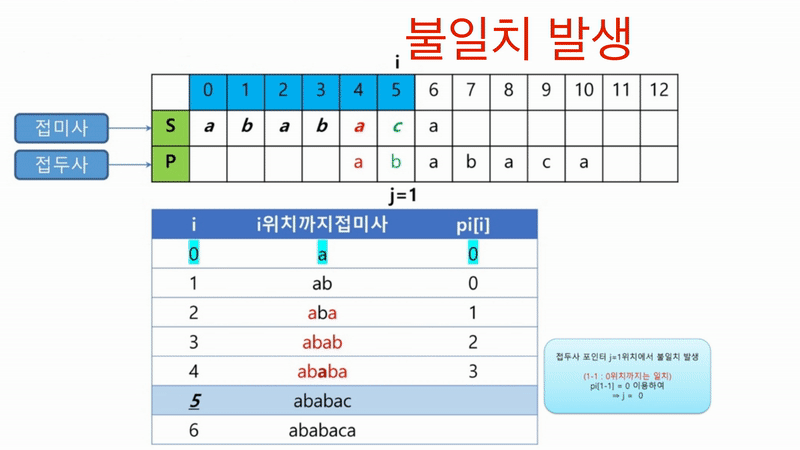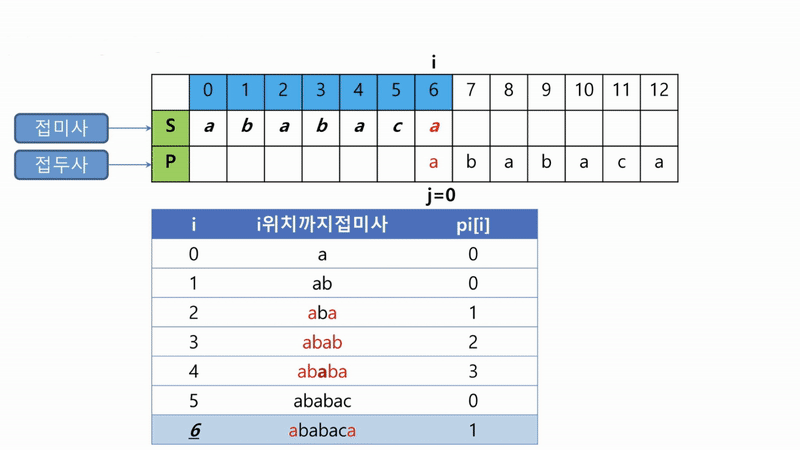
i번째 위치에서 불일치가 발생하면, i-1번째 위치까지는 일치한 것이기 때문에, pi[i-1]에 해당하는 위치부터 다시 탐색을 시작해야함을 알 수 있습니다.
부분일치 테이블을 만드는 방식은 다음과 같습니다.
방식 1
for(int i=1, j=0; i<pLength; i++){// i:접미사 포인터(i=1부터 시작, j:접두사 포인터
while(j > 0 && pattern[i] != pattern[j]) {
j = pi[j-1];
}
if(pattern[i] == pattern[j]) pi[i] = ++j;
}방식 2(KMP 알고리즘 적용)
//모든 접두사에대해 한꺼번에 계산하는 방식
int[] pi = new int[pLength];
int start = 1, partialMatched = 0;
while(start+partialMatched<pLength){
if(P[start+partialMatched]==P[partialMatched]){
++partialMatched;
pi[start+partialMatched-1] = partialMatched;
}else{
if(partialMatched == 0){
start++;
}else{
start += partialMatched-pi[partialMatched-1];
partialMatched = pi[partialMatched-1];
}
}
}문자열 탐색
탐색은 정말 간단합니다.
틀린 위치가 발생하면, pi[지금까지 맞은 문자의 갯수-1]에 해당하는 위치부터 탐색을 시작하게해주면 됩니다.
또한, 문자 패턴을 찾은 경우에는 시작 위치를 답의 리스트에 추가해야한다는 것을 제외하면 불일치가 발생한 경우와 같습니다.
리스트에 추가해준 다음, 문자열의 다음 위치와 비교를 하도록 포인터를 설정하고, 답이 될 수 있는 다음 후보인 패턴의pi[matched-1]째 위치부터 시작을 해주면 됩니다.
int matched = 0;
List<Integer> list = new ArrayList<>();
for(int i = 0;i<sLength;i++){
while(matched > 0 && S[i]!=P[matched]) matched = pi[matched-1];
if(S[i] == P[matched]){
++matched;
if(matched==pLength){
list.add(i-pLength+1);
matched = pi[matched-1];
}
}
}위의 코드는 아래와 같이 작동합니다.
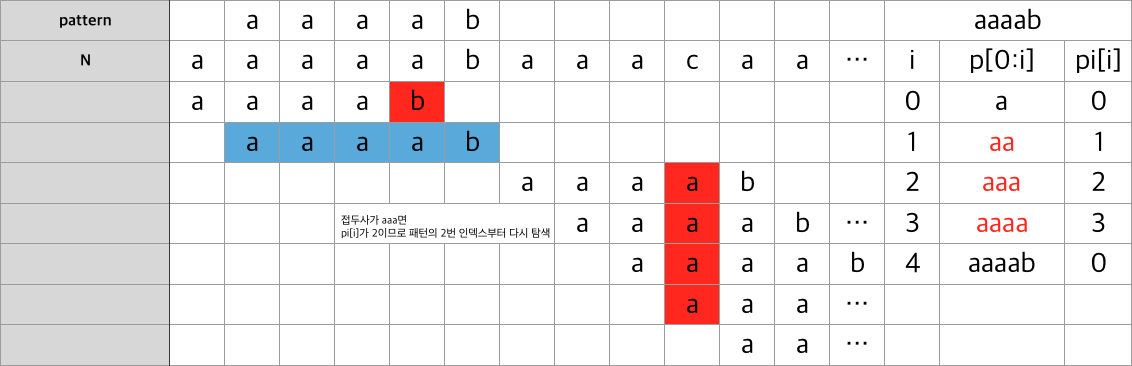
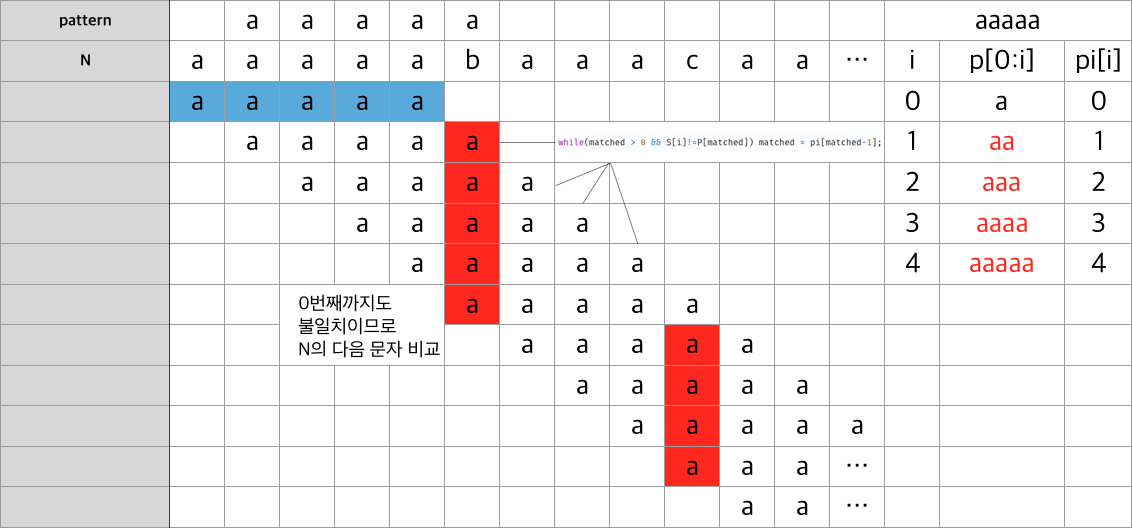
이런 식으로 안봐도 불가능하다고 판단되는 비교는 하지않아서 시간 복잡도를
O(N+M)(N(텍스트의 길이),M(패턴의 길이)) 까지 줄일 수 있습니다.
코드 구현
KMP 알고리즘을 적용하면 풀 수 있는 문제의 풀이를 보며 구현을 설명하겠습니다.
문제 보러가기
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class BOJ_1786 {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static char[] S,P;
static StringBuilder sb = new StringBuilder();
public static void main(String[] args) throws IOException {
S = br.readLine().toCharArray();
P = br.readLine().toCharArray();
int sLength = S.length,pLength = P.length;
if(pLength>sLength) {
System.out.println(0);
return ;
}
//부분 일치 테이블
int[] pi = new int[pLength];
int start = 1, partialMatched = 0;
while(start+partialMatched<pLength){
if(P[start+partialMatched]==P[partialMatched]){
++partialMatched;
pi[start+partialMatched-1] = partialMatched;
}else{
if(partialMatched == 0){
start++;
}else{
start += partialMatched-pi[partialMatched-1];
partialMatched = pi[partialMatched-1];
}
}
}
int matched = 0;
List<Integer> list = new ArrayList<>();
for(int i = 0;i<sLength;i++){
while(matched > 0 && S[i]!=P[matched]) matched = pi[matched-1];
if(S[i] == P[matched]){
++matched;
if(matched==pLength){
list.add(i-pLength+1);
matched = pi[matched-1];
}
}
}
sb.append(list.size()).append('\n');
for(int data : list){
sb.append(data+1).append('\n');
}
System.out.println(sb.toString());
}
}
