문제링크
풀이 전 계획 및 생각
맨 처음에는 array.sort()를 이용해서 해결을 했었다.
근데 직접 구현을 해보는 것도 좋을 것 같아서 merge sort를 이용해서 구현을 해보기로 했다.
merge sort를 고른 이유는 여러가지 정렬 알고리즘 중에서 퀵정렬과 병합정렬이 빠른데, 퀵정렬의 경우에는 worst case로 입력을 받을 경우에 시간초과가 생길 수 있을 것 같아서 병합정렬을 선택했다.
merge sort는 아래와 같이 작동한다.
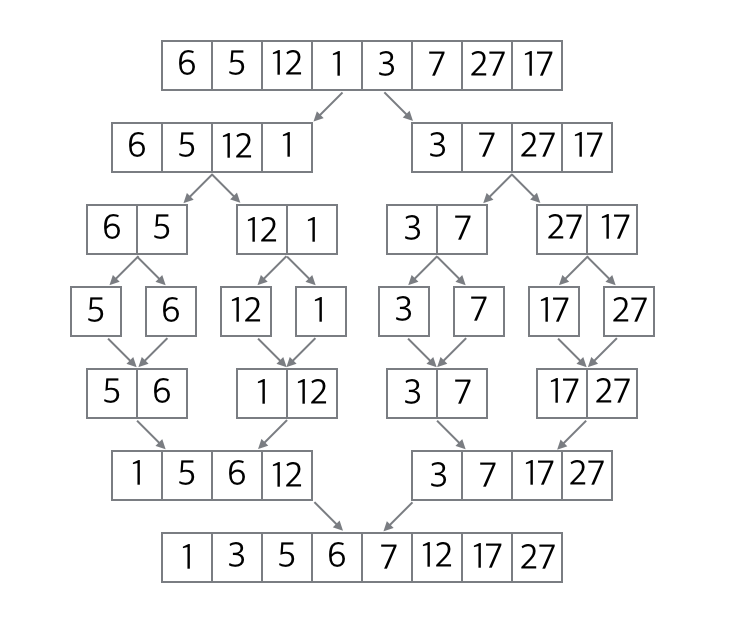
주어진 인풋을 반으로 나누는 과정을 반복하면서 길이가 1인 원소로 분할한다. 이 분할된 원소들을 정해진 순서에 맞게 합쳐준다.
원소의 개수가 홀수개인 경우에는 아래의 그림과 같은 순서의 연산과정을 통해서 정렬이 이루어진다.
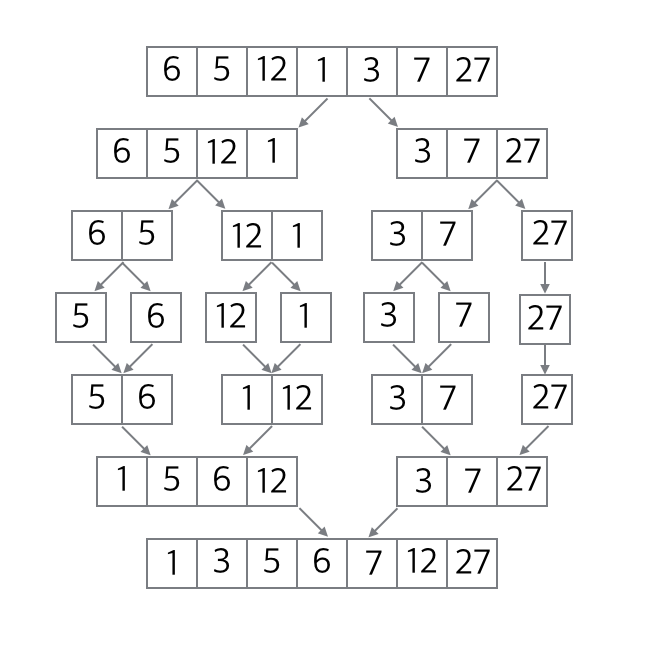
병합 정렬의 시간복잡도는 O(NlogN)이다.
N개의 원소를 가진 배열을 나누고 분할하는 연산이 logN(시간복잡도를 이야기할 때, log는 밑을 2로 하는 log라고 생각하는 것이 좋다.)번 실행된다.
거기에 비교 연산이 최대 N번 실행될 수 있기 때문에 병합 정렬의 연산의 최대 연산 횟수는 NlogN이다.
풀이
import sys
import math
def merge(sub_left_list,sub_right_list):
result = []
left = 0
right = 0
while left < len(sub_left_list) and right < len(sub_right_list):
if sub_left_list[left] < sub_right_list[right]:
result.append(sub_left_list[left])
left += 1
else:
result.append(sub_right_list[right])
right += 1
result += sub_left_list[left:]
result += sub_right_list[right:]
return result
def merge_sort(num_list):
if len(num_list) <= 1:
return num_list
mid = math.floor(len(num_list)/2)
sub_left_list = merge_sort(num_list[:mid])
sub_right_list = merge_sort(num_list[mid:])
return merge(sub_left_list, sub_right_list)
n = int(sys.stdin.readline())
array = []
for _ in range(n):
array.append(int(sys.stdin.readline()))
array = merge_sort(array)
for i in array:
print(i)풀이하면서 막혔던 점과 고민했던 점
시간 초과와의 싸움이였다. 이정도면 효율적이고 빠르겠지? 하면
처음에는 merge 함수에서 index를 옮기는 방식이 아니라 deque자료형을 이용해서 하나씩 꺼내는 방식으로 구현해보기도하고, list에 extend하는 방식도 사용해보고했지만, 역시 index를 옮기면서 하는게 가장 빨랐다.
list를 다루기위해서는 list의 주소에대한 접근과 list에대한 연산처리 시간이 소모되기 때문에, 효율적인 방법이 아니였다.
풀이 후 알게된 개념과 소감
deque 자료형에서는 slice를 하기위해서는 list에서 사용하는 방식(ex.array[start:end])이 아니라, itertools 라이브러리에 있는 islice를 이용해서 left = deque(itertools.islice(num_list,0,mid)) 와 같이 구현해야한다는 것을 알았다.
CPython에서는 정렬할 배열의 크기에 따라서 정렬 방식을 다르게한다는 것을 알았다.
행렬 곱셈을 할 때, 슈트라센 알고리즘을 적용하다가 크기가 어느정도 작아지면 일반 행렬 곱셈을 사용하는 것과 비슷한 아이디어인 것 같다.
이 아이디어를 알아두면 나중에 요긴하게 쓸 수 있을 것 같다.
