백 트래킹이란?
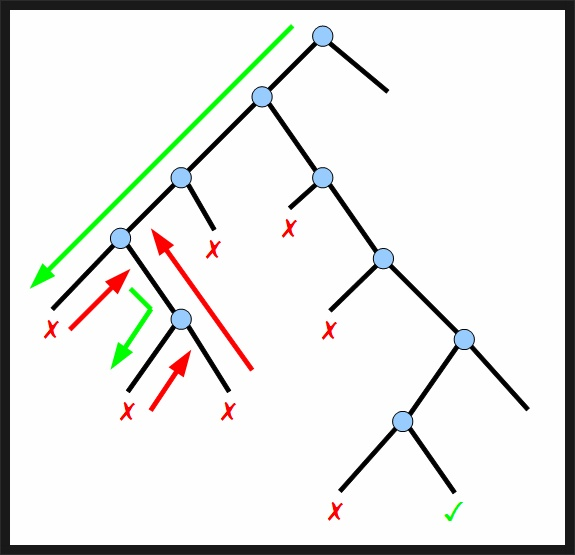
그래프 탐색 기법중 하나로 필요없는 경우를 가지치기를 해서 시간 복잡도를 줄이는 방법이다.
백트래킹에 대표적인 예제인 leetcode에 N-Queen 문제에 대해 알아보자
N-Queen 문제
n*n 체스판에 n개의 퀸이 서로 잡지 못 하는 경우의 수와 배열을 구하는 문제이다.
퀸은 체스에서 가로세로 대각선 길이 제한없이 잡을 수 있다.
Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
소스
def solveNQueens(n: int):
"""
이 문제를 풀기 위한 핵심아이디어는 visited 의 인덱스는 행, 값은 열을 나타낸다.
(1, 3)에 놓은 경우, visited[1] = 3 으로 표현하겠다는 것.
예시) n=4 이고 visited = [1, 3, 0, 2] 인 경우,
체스판을 그려보면 아래와 같다. (1이 퀸)
0 1 0 0
0 0 0 1
1 0 0 0
0 0 1 0
흔히 체스판이 2차원 배열이니 2차원 배열로 저장하는데 idx와 밸류를 각각 col row로 생각하면 시간 복잡도를 줄일 수 있다.
"""
answer = []
visited = [-1] * n
def is_ok_on(nth_row):
"""
n번째(nth) 행에 퀸을 놓았을 때, 올바른 수인지 검사한다.
nth 행의 퀸 위치와, 0번째 행부터 n-1번째 행까지 놓여진 퀸의 위치를 비교한다.
nth 행에 놓여진 퀸이 규칙을 깼다면 False 를 반환한다.
각 행에 퀸을 하나씩만 두고 검사하기 때문에 열과 대각선에 겹치는지만 검사하면 된다.
대각선 검사 : 0,0 ... 3,3 nth_row - row (행) == abs(visited[nth_row]) - visited[row] (열)
"""
for row in range(nth_row):
if visited[nth_row] == visited[row] or nth_row - row == abs(visited[nth_row]) - visited[row]:
return False
return True
def dfs(row):
if row >= n: #행이 n-1일 때까지 반복
grid = [['.'] * n for _ in range(n)] #그리드를 만드는 이유는 output으로 2차원 배열 형태기 때문에
for idx, value in enumerate(visited): #enumerate로 값이 있을때 Q로 변환
grid[idx][value] = 'Q'
result = []
for row in grid:
result.append(''.join(row)) #행을 string형태로 붙여줌
answer.append(result)
for col in range(n):
visited[row] = col #확인하고 있는 열 넣기
if is_ok_on(row): #위치가 맞다면 행 증가
dfs(row + 1)
dfs(0) #dfs(n)은 n번째 행을 검사할지를 말한다.
return answer이미지 출처:https://cinux.tistory.com/14