문제구분 방식

🔹 이분 탐색
조건을 만족하는 값 하나(target)를 빨리 찾기 위한 로그 시간 탐색 기법

🔹 투 포인터 & 슬라이딩 윈도우
부분합, 쌍 찾기, 구간 문제를 선형 시간에 푸는 기법

투 포인터(Two Pointer)

두 개의 점의 위치를 기록하면서 처리하는 알고리즘

시간복잡도: O(n)

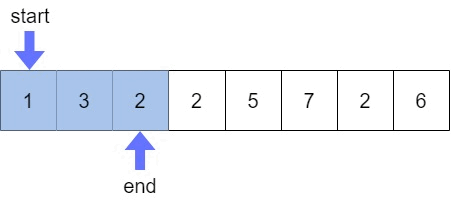
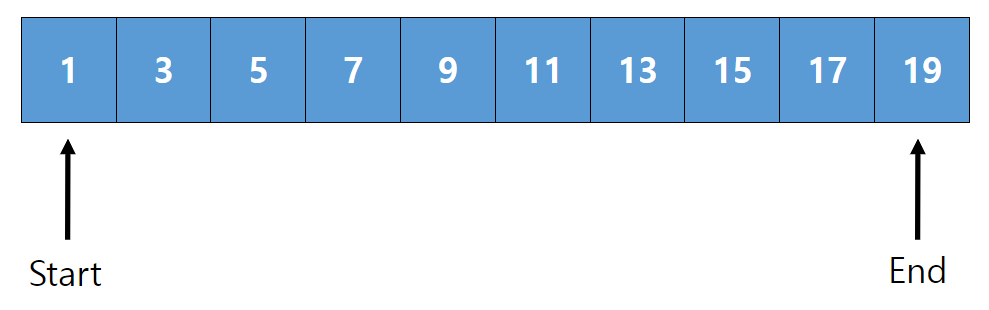
1. 양 끝에서 중간으로 이동하는 투 포인터

배열에서 특정 합이나 차를 만족하는 두 수 찾기

// 배열에서 특정 합을 가지는 두 수 찾기
function twopointer(nums, target) {
    let left = 0;
  	let right = nums.length - 1;
    
    while (left < right) {
        let sum = nums[left] + nums[right];
        
        if (sum === target) return [left, right]; // 정답 발견!
        else if (sum < target) left++; // 합이 작으면 left 이동
        else right--; // 합이 크면 right 이동
    }
    
    return [-1, -1]; // 없을 경우
}

2. 한 방향으로 이동하는 투 포인터(슬라이딩 윈도우)

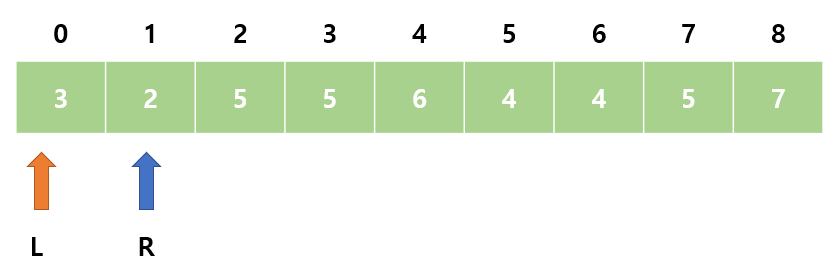
• 배열에서 중복 제거하기
• 포인터 두 개가 모두 왼쪽에서 시작해서 오른쪽으로 진행

// 배열의 중복을 제거한 원소의 갯수
function twopointer(nums) {
    if (nums.length === 0) return 0;
    let i = 0;
    
    for(let j = 1; j<nums.length; j++){
        if(nums[i] !== nums[j]){
        	i++;
        	nums[i] = nums[j];
        }
    }
  
  	return i+1;
}

🔍 슬라이딩 윈도우

크기가 고정된 프레임이 좌우로 움직이면서 프레임 안에 있는 데이터를 이용하는 알고리즘

• 시간복잡도: O(n)
• 고정된 크기의 연속된 부분배열을 다룰 때 사용
• 고정된 크기의 최대/최소 합, 평균, 곱 구할 때 사용

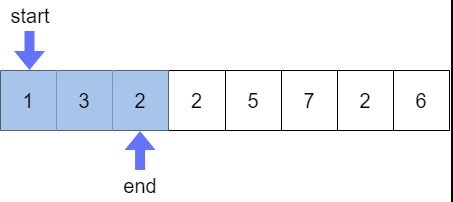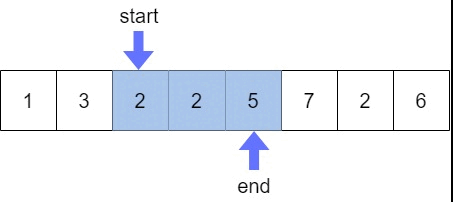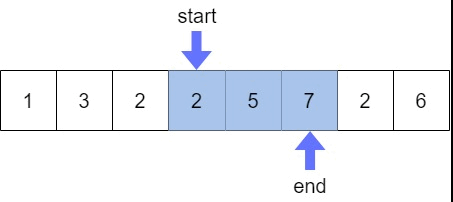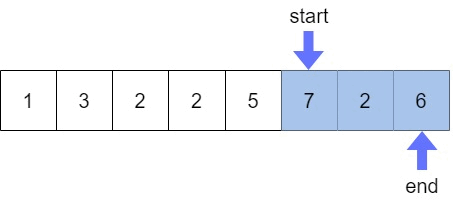
🔥슬라이딩 윈도우 코드

function slidingwindow(arr, k) {
  	let result = 0; // 길이 k의 부분 수열의 요소 전체 합의 최댓값
  	let sum = 0; // 특정 부분 수열의 전체 합

    for(let i = 0; i < k; i++) {
      sum += arr[i];
    }

    result = sum;

    for(let i = k; i < arr.length; i++) {
      sum += (arr[i] - arr[i - k]);
      result = Math.max(result, sum);
    }

    return result;
}

---

이분탐색(Binary Search)

탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법

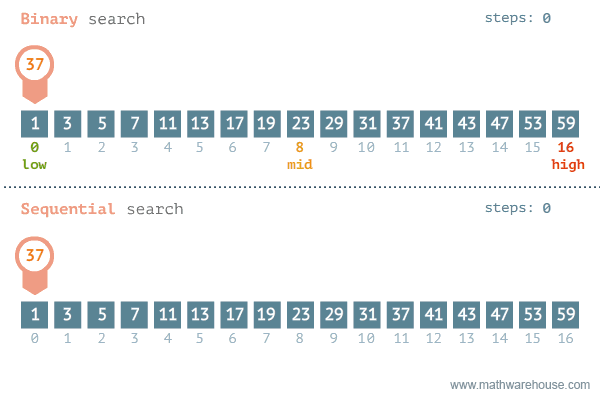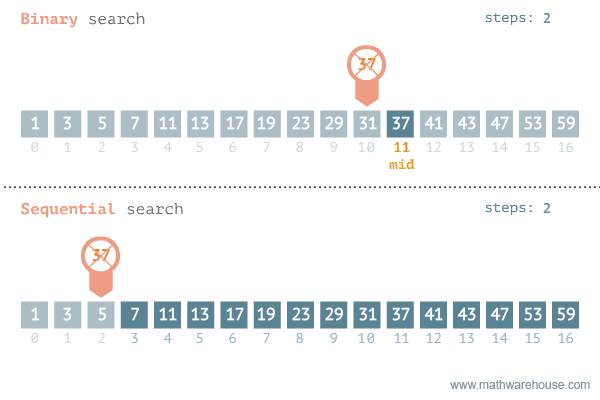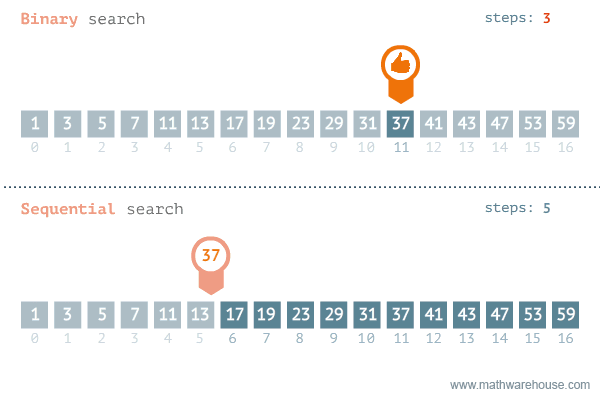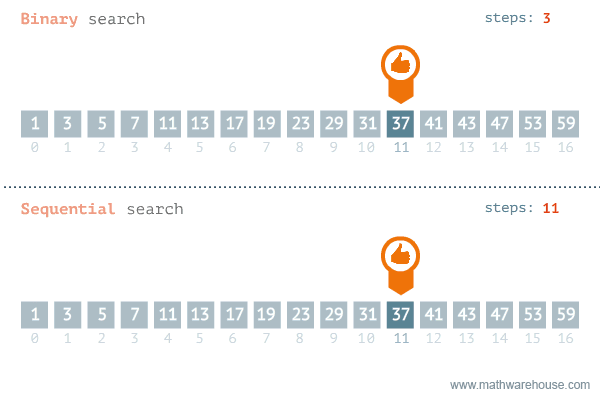
• 변수 3개(start, end, mid)를 사용하여 탐색한다.
  찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 찾는다.

• 시간복잡도: O(log₂n)

• 특정 값을 빠르게 찾을 때 사용

🔥이분탐색 코드

function binarysearch(nums, target) {
    let start = 0;
    let end = nums.length-1;

    while(start <= end){
        let mid = Math.floor((start+end)/2);
        if(nums[mid] === target){
            return mid;
        }else if(nums[mid] > target){
            end = mid - 1;
        }else{
            start = mid + 1;
        }
    }

    return start;  // 존재하는 값이 없다면 순서대로 삽입되었을 경우의 인덱스 반환
};