Central Limit Theroem

대학원 면접 준비를 하면서 처음 접해보는 개념이었다.

본인은 현재 확률과 통계를 고등학교 이후로 제대로 공부해본 적이 없어. 글이 다소 난해할 수도 있다는 점을 이해해주시길

참고 영상: 무작위 속 질서, 중심극한정리 | 확률과 통계

위의 영상에 정말 명확하고 간단하게 설명해준다.

본 글도 위의 영상을 뼈대로 내가 이해하기 편하도록 살을 붙여볼 계획이다.

확률 변수

먼저 Central Limit Theorem을 이해하기 위해서 확률변수를 간단하게 언급하자면,

영상에서와 동일하게 주사위를 예로 들어보자면, 각 면에서 나오는 숫자들을 확률 변수라고 생각하면 된다.(1,2,3,...6)

---

이제 확률 변수를 파악했으니, 간단하게 중심 극한 정리가 무엇인지를 말해보자면,

모집단에서 N개의 표본을 추출하였을 때, N이 무한에 가까운 수라는 가정하에 그 N개의 확률변수의 합의 분포는 가우시안 분포(종 모양의 분포)를 따르게 된다.

*분포를 히스토그램으로 나타냈을 때를 말한다.

이 정리가 신기한 점은 주사위 면이 나올 확률 분포가 균등한 분포 즉, 한면의 확률이 $\frac{1}{6}$가 아니더라도 많은 수의 표본을 추출하여 그 확률변수의 합을 분포로 나타내면 가우시안 분포의 형태로 나타나게 되는 것이다.

논리의 흐름이 좀 이상하긴 하지만 이해를 바라며,

일단 주사위 각 면이 나올 확률이 수학적 확률, uniform ditribution을 따르는 경우, 확률 변수의 합의 분포가 가우시안 분포를 따른다는 생각은 자명하다.

이단 우리가 확률변수의 분포를 따질 때, 영상을 참고해보면 각 확률 변수가 나올 수 있는 확률 들을 다 구해서 더하는 식으로 확률 분포를 만들어 낸다.

Ex. 주사위를 2번 던져서 7이 나올 확률.
$\frac{1}{6}*\frac{1}{6}(1,6)+\frac{1}{6}(2,5)+...+\frac{1}{6}(5,2)+\frac{1}{6}(6,1)=\frac{6}{36}$

이런 식으로 각 확률 변수의 확률을 구하여 히스토그램으로 분포를 표현하면, 두 주사위의 합이 7인 경우를 기준으로 종 모양이 만들어지는 것이다.

이런 방법으로 각 주사위의 면의 확률 분포가 uniform하지 않아도(통계적 확률) 우리는 확률 변수의 확률 분포를 구할 수 있는 것이다.

---

그럼 어떻게 주사위 면의 확률 분포가 uniform하지 않아도 확률 변수의 합의 확률 분포가 가우시안 분포를 따를 수 있는 지는 직관적으로 와닿지 않는다.

일단 먼저 이유를 말해주면, 확률 변수가 많아질 수록 확률 변수의 확률 분포는 점점 넓게 퍼지고 완만해지기 때문인데,

이를 이해하기 위해서 먼저, 평균 $\mu$와 표준 편차 $\sigma$에 대해서 알아볼 필요가 있다.

먼저, 우리는 확률 변수의 평균을 어떻게 구할 수 있을까? 많은 사람들이 평균을 구하는 방법은 당연하게도
이전에 말했던 수학적 확률은 사건을 시행해보지 않고 이렇게 나올 것이다 기대하고 구하는 확률이다.(만약 실제로 주사위를 6번 던진다고 했을 때, 각 면이 무조건 한번씩 나오지는 않는다.)

그리하여 우리는 그에 대한 평균을 역시 시행했다고 가정하고 기대할 수 있는 평균값이라고 생각해서 기댓값이라고 부른다.

$\mu=E[X]=\sum_xp(X=x)\cdot x$

이 공식을 통해서 우리는 평균을 구할 수 있다.

그리고 분산은 분포가 퍼져있는 정도를 측정하는 방법인데, 분포를 나타내는 그래프가 얼마나 퍼져있는 지를 파악할 수 있는 수치라고 생각한다.

$Var(x)=E[(X-\mu)^2]=\sum_xp(X=x)\cdot(x-\mu)^2$

로 구할 수 있다. 하지만 이건 제곱으로 되어있기에 거리의 개념으로 생각하기는 어렵다. 어느 정도 퍼져있는 지를 파악하기에는 거리가 더 적합하므로 우리는 분산에 제곱근을 씌운 표준편차를 이용한다.

$\sigma = \sqrt{Var(x)}$

이렇게 평균과 표준편차를 구하는 공식을 보면, 자명하게도 확률 변수의 개수, 즉 주사위를 던지는 횟수가 많아지면 많아질 수록 평균의 값도 비례하여 많아지는 것을 알 수 있을 것이다.

Ex. 주사위 하나만 던졌을 때, 기댓값
$E(X) = \frac{1+2+3...+6}{6}=3.5$
주사위 2개를 던졌을 때, 기댓값
$E(X_1+X_2) = \frac{2\cdot 1+3\cdot 2...+11\cdot 2+12\cdot 1}{36} = 7 = E(X_1)+E(X_2)$

정확히 2배가 오른 것을 확인할 수 있다. 같은 확률 분포에서 나온 것이기에 $X_1$(처음 주사위 던졌을 때)와 $X_2$(두번째)는 같은 기댓값 3.5를 가지는 것을 확인할 수 있다.

고로, $X_1+X_2+...+X_N$의 기댓값은 $N\cdot E(X_1)$으로 나타낼 수 있는 것이다.

비슷한 논리로 $X_1+X_2+...+X_N$의 분산은 $N\cdot Var(X_1)$로 나타낼 수 있고, 표준 편차는 $\sqrt{N}\cdot \sigma$로 나타낼 수 있는 것이다.

---

사실 나는 이게 중심 극한 정리의 실마리라고 생각한다. 확률 변수의 개수가 많아짐으로써 점점 평균이 오른쪽으로 가게되고 표준 편차가 증가함으로써 그래프는 점점 완만해지기 때문에, 결국 그래프의 변화들을 하나의 평균에 맞추고 표준 편차를 1로 맞춰주면 가우시안 분포의 형태에 수렴하게 되는 것이다.

이제 이러한 성질을 생각하면서, 가우시안 분포의 수식을 살펴보자.

먼저 $e^x$와 $e^{-x}$의 그래프를 보면

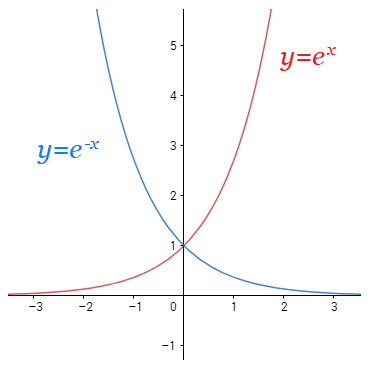
이런 그래프가 나오고 $e^{-|x|}$ 이런 식으로 절대값을 씌우면 가운데 뾰족한 그래프만 남게된다.

절대값을 씌우면 그래프가 뾰족한 모양이 되는데 그걸 $e^{-x^2}$의 식으로 만들면

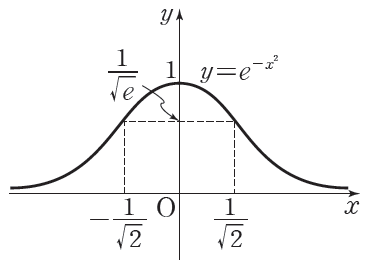
이런 그래프가 나오게 된다.

이 그래프의 넓이를 조절하기 위해서 $-x^2$ 앞에 상수항을 붙여서 $e^{-cx^2}$ 이렇게 표현해주면 c의 크기에 따라 종모양이 넓어지기도하고 좁아지기도 한다.(밑 e의 크기를 조절하는 것과 같은 맥락이다.)

우리는 저 넓이를 $\sigma$로 나타내고 싶기 때문에, $-\frac{1}{2\sigma^2}$를 x에 곱해서 $e^{-\frac{1}{2}(\frac{x}{\sigma})^2}$로 나타내준다.

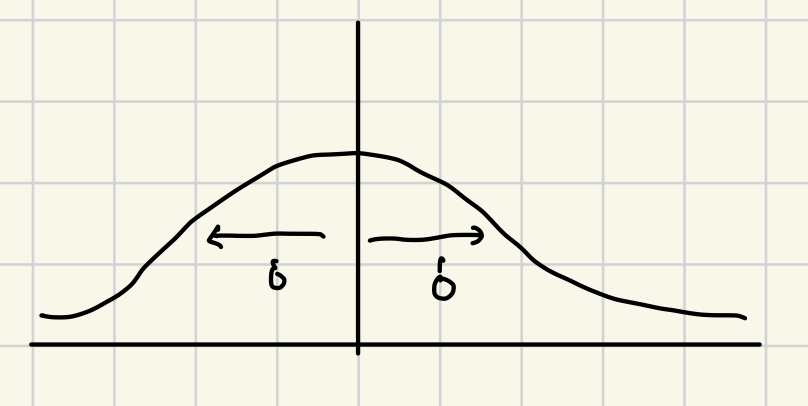
이렇게 우리는 표준편차의 크기가 그래프에 어떤 영향을 미치는 지 확인할 수 있다.

이산 확륣 분포와 다르게 연속 확률 분포는 한 점에 대한 확률을 구할 수 없다(Ex. 169와 170사이에서 170일 경우를 생각해보면, 두 수 사이에 실수는 무한히 존재하므로 확률은 0이됨.)고로, 두 점 사이의 구간에 대한 확률(두 점 사이의 그래프의 넓이)로 물어봐야한다. 그리고, 확률의 성질을 고려했을 때, 항상 그래프 전체의 넓이는 1이 되어야 한다.

현재 그려진 그래프의 넓이: $\sqrt{2\pi}\sigma$

고로, 우리는 원래 식에 저정도로 나눠줘서 그래프의 넓이를 1로 맞춰줘야한다.(그래야, 확률 분포의 관점에서 그래프를 볼 수 있으니까)
=> $\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}(\frac{x}{\sigma})^2}$

또한, 중앙은 평균 $\mu$가 되길 바라기 때문에, x에서 $\mu$를 빼준다.
=> $\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2}$

그렇게 하면 우리가 아는 가우시안 분포의 수식이 된다.

결국 X(확률 변수)가 하나일 때는, => $\mu, \sigma$이렇게 존재한다면,

$X_1 +X_2+...+X_N$인 경우, => $N\cdot \mu, \sqrt{N} \sigma$ 이렇게 되기에
=> $\frac{1}{\sqrt{2\pi}\sqrt{N}\sigma}e^{-\frac{1}{2}(\frac{x-N\cdot \mu}{\sqrt{N}\sigma})^2}$

위에서 말한 걸 기억해보면, 결국 확률변수가 많아질 수록 표준편차의 값도 비례하게 커져서 그래프는 좀 더 완만해지고 중심은 계속 오른쪽으로 이동하게 되는 것이다.

그리고 우리는

• $\frac{X_1+X_2+...+X_N)-N\cdot \mu}{\sigma \cdot \sqrt{10}}$

을 통해서 평균을 0으로 표준편차를 1로 맞춰준 식을 구할 수 있다.

이걸 표준 확률 분포라고 하는데 이런 표준화된 정규 분포는 $X_1+...+X_N$와 평균 사이의 간격을 표준편차 단위로 표현할 수 있다.

결국 확률 변수의 크기가 클 수록 그래프의 모양은 가우시안 분포의 모양에 가까워지게 된다.

이걸 왜사용할까? 우리는 이러한 중심 극한 정리를 통해서

$lim_{N->\infty}p(a<\frac{(X_1+...+X_N)-N\cdot \mu}{\sigma \sqrt{N}}<b)=\int^b_a\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx$

이렇게 특정한 값이 특정 구간 내에 있을 확률을 구해낼 수 있다. 참고로 표준 정규분포 형식으로 맞춰줘서 구해준다.

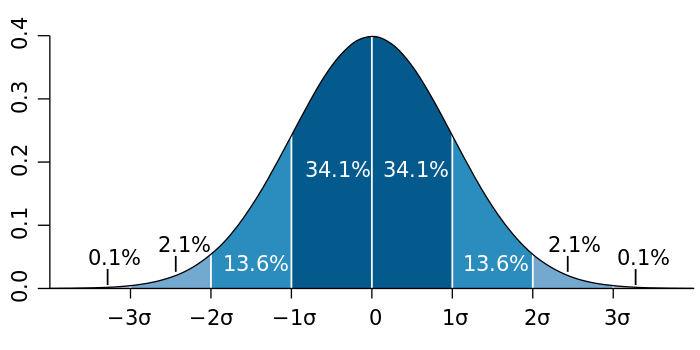
• 산뢰구간 68%는 평균에서 1 표준편차 내에 위치한다.
• 신뢰구간 95%는 평균에서 2 표준편차 내에 위치한다.
• 신뢰구간 99.7%는 평균에서 3 표준편차 내에 위치한다.
  

이러한 전제를 생각해보면서,

각 면이 같은 확률을 갖는 주사위를 100번 굴려 나온 숫자들을 모두 더하는 상황을 가정해보자. 여기서 결과의 합계가 신뢰구간 95%에 속할 때 그 구간은?

1. 초기 분포의 평균 구하기

• $\mu = (1+2+3+4+5+6)\cdot \frac{1}{6}=\frac{21}{6}=3.5$
• $Var(X) = \frac{1}{6}((1-3.5)^2+...+(6-3.5)^2)=2.92$
• $\sigma=\sqrt{2.92}=1.71$

2. 100개의 주사위를 던진 경우,

• $\mu=100*3.5=350$
• $\sigma = \sqrt{100}*1.71=17.1$

우리는 위에서 보았던 식에서 표준 정규 분포에서 a와 b는 -2와 2인 걸 알 수 있다. 이제 이걸 표준화 하기 전에 값으로 구해보면.

• $a = -2*\sqrt{N}*\sigma + N*\mu=-2*17.1+350=316$
• $b = 2*\sqrt{N}*\sigma + N*\mu=2*17.1+350=384$

로 구할 수 있게 된다.

다르게 생각해보면, 만약 우리가 구간을 가지고 있다면, 그 구간이 어떤 신뢰구간에 포함되는 지를 확인할 수 있다.

그리고 마지막으로 중심극한 정리를 위한 3가지 가정이 존재한다.

1. 모든 확률 변수 $X_i$는 독립이다.
2. 각각의 $X_i$는 같은 확률 분포에서 유래한다.(Ex. 균일 분포를 따르는 주사위에서 표본을 추출함)
3. 0 < Var(x) < $\infty$, 계산된 분산의 값은 유한한 값을 가져야한다.