[확률과 통계] Lecture 1: Probability and Counting

원본 영상: Lecture 1: Probability and Counting | Statistics 110

숫자와 식으로 표현하기 전에 말로 설명할 수 있는지, 그리고 왜 그렇게 생각하게 되었는 지를 고민해보자.

확률(probability): 모든 일어날 수 있는 경우의 수 가운데 어떤 일이 일어날 가능성
Ex) Gambling(Dice & Cards)
통계(stastic): 불확실성의 논리
-> 불확실성을 정량화 하자.

• sample sapce: 하나의 실험에서 나올 수 있는 모든 가능한 결과들의 집합
• event: sample space의 부분 집합

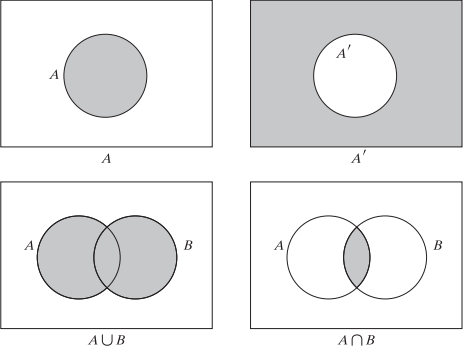
Ex. 만약 우리가 2개의 주사위를 굴리는 실험을 한다고 하면, 우리의 표본 공간의 집합의 수는 36이 나옴. 그리고 사건은 그 36개의 가능한 결과중에 부분 집합이라고 볼 수 있다.

Naive Definition of Probability

$P(A) = \frac{\text{the number of favorable outcomes}}{\text{the number of possible outcomes}}$

• P: probability
• A: event

Ex) 동전을 2번 던지면, 4개의 결과가 나올 수 있고 둘다 앞면이 나올 확률을 따져보면 $\frac{1}{4}$로 볼 수 있는 거임.
=> 여기에는 숨겨진 가정이 있는데, 앞면과 뒷면이 나올 가능성이 같다는 것이다. 즉, 모든 결과가가 나올 확률이 같다는 것. 그리고 유한한 표본 공간에 존재한다는 것을 가정한다.
-> 이런 가정들은 대칭의 성질을 갖는 문제들(ex. 주사위)에서 합리적인 가정이된다.

How do we count?

우리는 확률을 구하기 위해 어떻게 표본 공간의 수와 사건의 수를 셀 수 있을까?

• Multiplication Rule for Counting => 하나의 실험에 대해 $n_1$만큼 가능한 결과값이 나왔다고 가정하고, 첫 번째 실험의 결과 $n_1$에 대해서 두 번째 실험의 결과는 $n_2$만큼 가능한 결과값이 나오고... r번째 실험의 결과는 $n_r$만큼 가능한 결과값이 나오면, 전체 결과값은 $n_1*n_2*n_3*...*n_r$ 만큼 나온다고 계산할 수 있다.

Ex_1. 아이스크림을 고를 때, 콘의 종류가 2개있고 아이스크림의 맛의 종류가 3개 있으면, 총 결과의 수는 6개가 나올 수 있다.
(여기서 실험의 순서는 콘을 고르는게 먼저가 될 수도, 아이스크림의 맛을 고르는게 먼저가 될 수도 있다.)

• Binomial Coefficient(이항 계수): 이항식을 이항정리로 정리했을 때, 나오는 각 항의 계수. 더 쉽게 말하면 이항식을 n제곱 했을 때, 각 항의 계수들을 말한다.
  
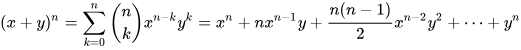
  이항 계수는 $\binom{n}{k}=\frac{n!}{(n-k)!k!}$, 0 if k > n 로 구할 수 있다.
  그리고 이건 다르게 말하면, 순서가 상관이 없을 때,하나의 그룹 n명의 사람이나 물건 중 k개를 고르는 경우의 수라고 말할 수 있다.
  

  n개 중에 k를 고르는데 순서가 상관이 없으면 처음에는 n개, 그 후에 n-1개... n-k+1개까지 고를 수 있다. 하지만 여기서 순서가 상관이 없어서 중복이 발생하기에 그 중복을 제거하기 위해 k!으로 나누는 것이다. (k개의 자리가 있을 때 순서를 변경하는 경우의 수는 k!이기 때문에.)

Ex_2. 포커에서 풀 하우스(3개, 2개가 각각 똑같은 모양)가 나올 경우의 수.

• 첫번째 3개의 카드가 같은 모양일 경우의 수 $13* \binom{4}{3}$
• 두번째 2개의 카드가 같은 모양일 경우의 수 $12* \binom{4}{2}$
  
  고로 전체 경우의 수는 $13* \binom{4}{3} * 12* \binom{4}{2}$이다. (순서가 바뀌어도 상관 없음)
  여기서 확률을 구하려면 표본 공간이 필요함. 이 실험에서의 표본 공간은 결국 전체의 카드에서 5개의 카드를 뽑는 경우의 수가 될 수 있는 거임.
  고로, 표본 공간의 수는 $\binom{52}{5}$가 된다.
  풀하우스가 나올 확률: $\frac{13* \binom{4}{3} * 12* \binom{4}{2}}{\binom{52}{5}}$

Sampling Table

	Order Matters	Order Doesn't Matter
Replacement	$n^k$	$\binom{n+k-1}{k}$
Without Replacement	$\frac{n!}{(n-k)!}$	$\binom{n}{k}$

• Order matter: 순서가 중요한가
• Replacement: AA가 나올 수 있는가?