
On.
Algorithm
1. 수도코드
0) 문제 유형 파악: 하노이의 탑 처럼 비슷한 동작을 반복하는 것들은 재귀함수로 푼다!
- 출발지의 가장 밑에 있는 판이 도착지의 가장 밑으로 이동하려면, 출발지에서 가장 밑의 판을 제외한 나머지 판들이 전부 보조에 있어야한다.
- 재귀 함수 문제는 잘게 쪼개서 제일 작은 사이즈 부터 그려보며 규칙을 파악하는 것이 좋다.
- 규칙을 찾았으면 식이든, 순서든 일반화를 시킨다.
- 근데 그게 잘 안되니까 연습하자...ㅎㅎ
1) 출발지에 있는 판중에 가장 밑에 있는 판을 제외한 나머지 판들을 보조에 놓는다. (재귀함수)
- 재귀함수가 돌면서 출발지에 있던 가장 밑의 판을 제외한 나머지 판들이 보조에 차례로 쌓이는 작업이 수행된다.
- 그림 설명
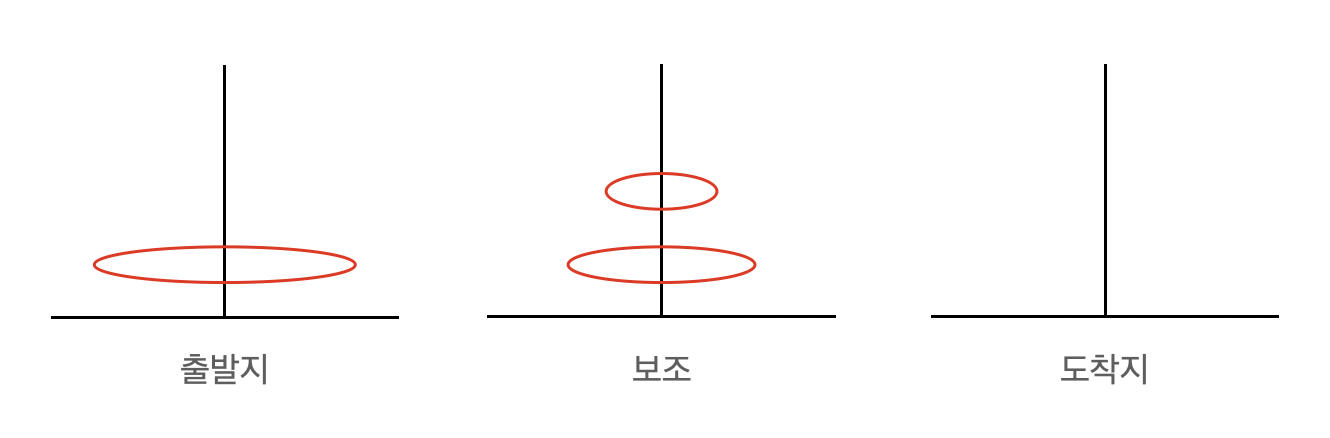
2) 가장 밑 판을 도착지에 놓는다. (answer에 추가)
- 그림 설명
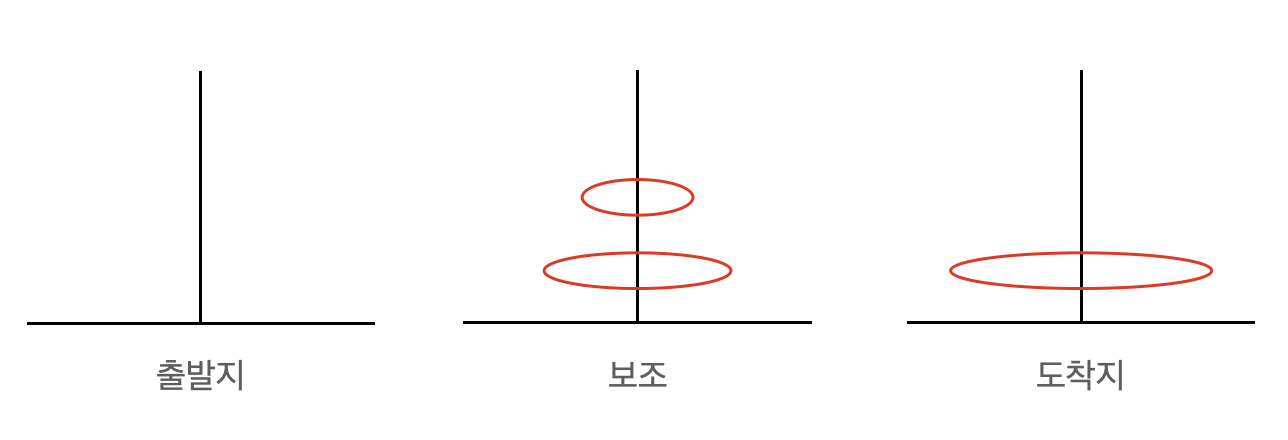
3) 보조에 있는 판들을 도착지에 옮긴다. (재귀함수)
- 재귀함수가 돌면서 보조에 있던 판들이 도착지에 차례로 쌓이는 작업이 수행된다.
- 그림 설명
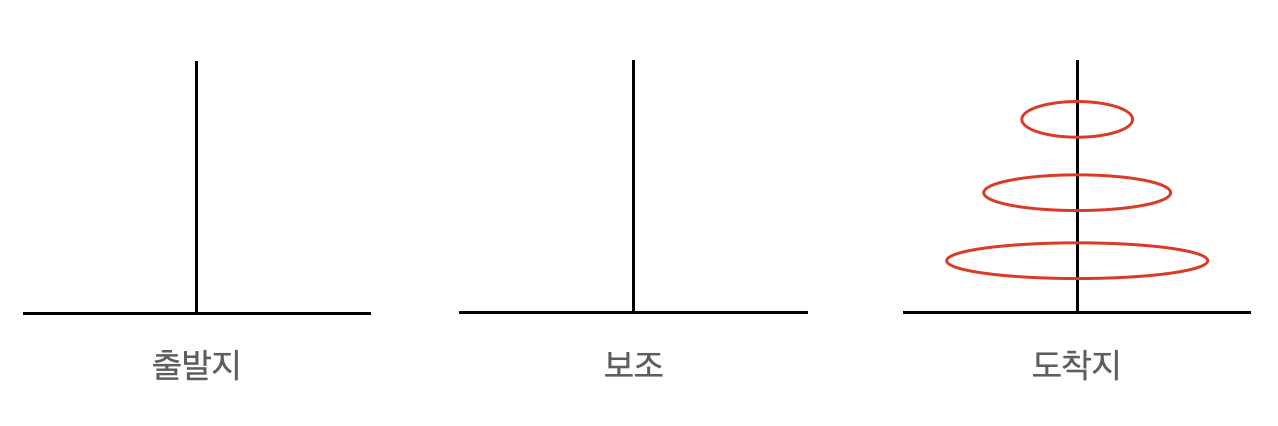
4) 종료 조건으로 n=1이 되면, 출발지에 있는 판을 도착지로 옮긴다.
- 때에 따라 출발지가 보조가 될 수도 있고, 도착지가 될 수도 있다.
- 때에 따라 도착지가 출발지가 될 수도 있고, 보조가 될 수도 있다.
- 때에 따라 보조가 출발지가 될 수도 있고, 도착지가 될 수도 있다.
- 위에 1, 2, 3번을 명확히 이해하면, 방금 한 소리가 무슨 말인지 이해가 된다...ㅎㅎ
2. 구현코드
def hanoi(n, start, to, mid, answer):
if n == 1:
return answer.append([start, to])
hanoi(n-1, start, mid, to, answer)
answer.append([start, to])
hanoi(n-1, mid, to, start, answer)
def solution(n):
answer = []
hanoi(n, 1, 3, 2, answer)
return answer3. 배운점
- 재귀는 트리 형태로 코드를 직접 손으로 써가면서 풀자!
4. 참고
- 얄팍한 코딩사전 👈 클릭!
