[자료구조]Heap

Heap이란?

• 힙(Heap)은 최대값이나 최소값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전 이진 트리(Complete Binary Tree)를 기본으로 한 자료구조이다.
• 조건을 만족하는 정렬만 해뒀다 (느슨한 정렬)
  • 완전 정렬 -> [1, 2, 3, 4, 5, 6, 7]
  • 느슨한 정렬 -> [1, 3, 2, 7, 4, 6, 5]

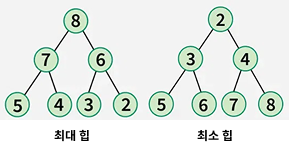
Heap의 종류

• 최대 힙 (Max Heap)
  • 부모 노드의 키 값이 모든 자식 노드의 키 값보다 항상 크거나 같은 이진 트리
  • 부모 노드 >= 자식 노드
• 최소 힙 (Min Heap)
  - 부모 노드의 키 값이 자식 노드의 키 값보다 항상 작거나 같은 이진 트리
  - 부모 노드 <= 자식 노드
  
  데이터의 삽입과 삭제에 걸리는 시간 복잡도는 O(logN) 이다

구현

heap의 대표적인 기능으로는 3가지가 있다

• insert(삽입)
• delete(루트값 반환)
• peek(루트값 확인)

알고리즘에서 가장 활용성이 높은 Min Heap을 구현해 보겠다.

Insert (삽입)

• Heap 에 새로운 값을 추가한다
• 새로 추가한 위치를 기반으로 부모 노드와 값을 비교해 부모 노드의 값이 크다면 위치를 변경한다
• 이전 단계를 반복하면서 부모노드가 더 작은 값이 나올때까지 반복한다.

  // 새로운 값을 추가 후 정렬 (bubble up)
  insert(value) {
    this.heap.push(value) // 새로운 노드 추가
    this.bubbleUp( this.heap.length -1 ) // bubble up 정렬
  }

  bubbleUp(idx) {
    while ( idx > 0 ) {  
      const parentIdx = Math.floor((idx-1)/2) // 부모 노드 계산
      // 자식 노드가 부모 노드보다 작을 경우
      if ( this.heap[parentIdx][1] > this.heap[idx][1] ) {
        // 자식과 부모 노드 위치를 바꿈
        [ this.heap[idx], this.heap[parentIdx] ] = [ this.heap[parentIdx], this.heap[idx] ]
        idx = parentIdx // 인덱스를 부모 노드의 인덱스로 교체
      } else { // 정렬 완료
        break
      }
    }
  }

Delete (루트값 반환)

• 루트 노드를 제거한다
• Heap에서 맨 마지막의 노드를 루트로 이동 시킨다
• 자식 노드와 값을 비교하면서 자식 노드의 값이 작다면 가장 작은 노드와 위치를 교환한다
• 이전 단계를 반복하며 모든 자식 노드의 값이 자신보다 작을때까지 반복한다

  // 루트 값을 반환 후 정렬 (bubble down)
  delete() {
    // Heap에 값이 하나뿐이면 pop()으로 바로 반환
    if (this.heap.length === 1) return this.heap.pop()
    
    const min = this.heap[0]
    this.heap[0] = this.heap.pop() // 마지막 노드를 루트로 이동
    this.bubbleDown(0) // bubble down 정렬
    return min // 최소값 return
  }

  bubbleDown(idx) {
    const length = this.heap.length // 힙의 범위
    while (true) {
      let smallest = idx // 현재 노드의 index
      const left = idx * 2 + 1  // 왼쪽 자식 노드의 index
      const right = idx * 2 + 2  // 오른쪽 자식 노드의 index

      // 범위를 벗어나지 않으면서 현재 노드 보다 왼쪽 자식 노드가 작을 경우
      if ( left < length && this.heap[left][1] <this.heap[smallest][1] ) {
        smallest = left
      }
      // 범위를 벗어나지 않으면서 현재 노드 보다 오른쪽 자식 노드가 작을 경우
      if ( right < length && this.heap[right][1] < this.heap[smallest][1] ) {
        smallest = right
      }

      // 현재 노드보다 작을 자식 노드가 있었을 경우 교체
      if ( smallest !== idx ) {
        [ this.heap[smallest], this.heap[idx] ] = [ this.heap[idx], this.heap[smallest] ]
        idx = smallest
      } else { // 없을 경우 종료
        break
      }
    }
  }

Peek (루트 값 확인)

  // 루트 값 확인
  peek() {
    return this.heap[0] ?? null 
  }

전체 코드

class MinHeap {
  constructor() {
    this.heap = []
  }

  // 새로운 값을 추가 후 정렬 (bubble up)
  insert(value) {
    this.heap.push(value) // 새로운 노드 추가
    this.bubbleUp( this.heap.length -1 ) // bubble up 정렬
  }

  bubbleUp(idx) {
    while ( idx > 0 ) {  
      const parentIdx = Math.floor((idx-1)/2) // 부모 노드 계산
      // 자식 노드가 부모 노드보다 작을 경우
      if ( this.heap[parentIdx][1] > this.heap[idx][1] ) {
        // 자식과 부모 노드 위치를 바꿈
        [ this.heap[idx], this.heap[parentIdx] ] = [ this.heap[parentIdx], this.heap[idx] ]
        idx = parentIdx // 인덱스를 부모 노드의 인덱스로 교체
      } else { // 정렬 완료
        break
      }
    }
  }

  // 루트 값을 반환 후 정렬 (bubble down)
  delete() {
    // Heap에 값이 하나뿐이면 pop()으로 바로 반환
    if (this.heap.length === 1) return this.heap.pop()
    
    const min = this.heap[0]
    this.heap[0] = this.heap.pop() // 마지막 노드를 루트로 이동
    this.bubbleDown(0) // bubble down 정렬
    return min // 최소값 return
  }

  bubbleDown(idx) {
    const length = this.heap.length // 힙의 범위
    while (true) {
      let smallest = idx // 현재 노드의 index
      const left = idx * 2 + 1  // 왼쪽 자식 노드의 index
      const right = idx * 2 + 2  // 오른쪽 자식 노드의 index

      // 범위를 벗어나지 않으면서 현재 노드 보다 왼쪽 자식 노드가 작을 경우
      if ( left < length && this.heap[left][1] <this.heap[smallest][1] ) {
        smallest = left
      }
      // 범위를 벗어나지 않으면서 현재 노드 보다 오른쪽 자식 노드가 작을 경우
      if ( right < length && this.heap[right][1] < this.heap[smallest][1] ) {
        smallest = right
      }

      // 현재 노드보다 작을 자식 노드가 있었을 경우 교체
      if ( smallest !== idx ) {
        [ this.heap[smallest], this.heap[idx] ] = [ this.heap[idx], this.heap[smallest] ]
        idx = smallest
      } else { // 없을 경우 종료
        break
      }
    }
  }

  // 루트 값 확인
  peek() {
    return this.heap[0] ?? null 
  }
}

우선 순위 큐(PriorityQueue) 와 Heap 의 관계

• 우선 순위 큐는 ADT(Abstract Data Type(추상 자료형))으로 Heap은 우선 순위 큐를 구현한 자료구조이다 (heap 말고 다른 구현 방법도 있다)
  • ADT - 자료가 어떻게 저장되고, 어떤 연산이 가능한지를 정의만 해 놓은 개념