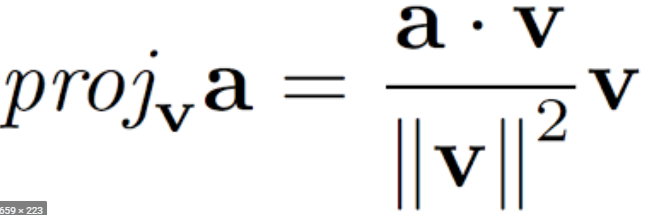[TIL] Day 7 - 인공지능 수학(3)

와.. 수학공식 마크다운 신세계다..
※ 마크다운 수학기호 참고 블로그
https://bit.ly/3aT4d42

vector의 이해

n-vector는 크기와 방향을 가진 물리량 -> 길이 x 방향

• v = (v1,v2,v3, ... ,vn)
• v의 크기(길이) = √v1^2+v2^2+,..., vn^2
• v의 방향 = 1/||v|| x v (길이를 1로 취한 값 -> 방향만 남는다)

vector의 내적(inner product)

벡터 u,v에 대한,
i) 좌표계 없이 표현
u · v = ||u|| x ||v|| x cosθ
ii) 좌표계 상에서 표현
u = (u1,u2,...,un), v = (v1,v2,...,vn) 일때,
u · v = u1 x v1 + u2 x v2 + , ... , + un x vn

내적의 결과는 무조건 스칼라다

※ 참고 유튜브 강의
https://www.youtube.com/watch?v=IOf1o72aKDc

vector의 직교(orthogonal)

두 벡터 u,v 간의 내적이 0이면, 직교(orthogonal)이다.
θ = 90 -> cos 90° = 0 -> u · v = 0

※ 물리적 의미
u,v가 직교할 때, udml 방향으로의 전진은 v방향에서 전혀 측정되지 않는다.
-> 완전 독립적이다. 수선의 발을 놓을 수 없다.

투영(Projection)

두 벡터 v,a가 있을 때, 벡터 a를 v위에 투영한 벡터를

또한 벡터 u를 a위에 투영하고 남은 보완벡터(complement vector)는 'a-projv(a)'
이때 투영한 벡터와 보완벡터는 직교한다. -> 벡터 a를 직교 분할 가능하다.

직교 행렬(orthogonal matrix)

주어진 행렬의 모든 열벡터가 서로 직교한다면, 그 행렬을 직교행렬이라고 한다.
-> 직교행렬은 곧 직교 좌표계를 의미한다.
(행렬은 각 열벡터가 기저(basis)를 이루는 좌표계이기 때문에)

직교행렬을 이용한 선형시스템

: 선형시스템 Ax=b에서 A가 직교행렬이라면 A의 역행렬 없이 해를 구할 수 있다.

• x의 i번째 요소는 투영으로 구할 수 있다.

정규직교 행렬(orthonormal matrix)

주어진 행렬이 직교행렬이고 모두 열벡터의 크기가 1이라면(방향만 남았다면),
그 행렬은 정규직교행렬 이라고 한다.

정규직교행렬을 이용한 선형시스템

: 선형시스템 Ax=b에서 A가 정규직교행렬이라면 A의 역행렬 없이 해를 구할 수 있다.

• x의 i번째 요소는 내적으로 구할 수 있다.

QR 분해 (직교 분할)

A = QR , Q = 정규직교행렬, R = 나머지(후삼각행렬)

QR분해를 이용한 Ax=b 를 나타내면,

Ax=b -> (QR)x=b -> Q(Rx)=b -> (1)Qy=b -> (2)Rx=y
(1) 내적(inner product)로 y 구하기
(2) Back-substitution(후방대치법)으로 x 구하기

※ QR vs LU

• LU는 선형시스템을 풀 때, 병렬처리 X -> 느리다.
• QR은 Q행렬이 꽉찬 구조이기 때문에 공간 사용량이 많다.
• LU와 QR 모두 n x n 정방행렬만 가능하다!

SVD(Singular Value Decomposition) 특이값 분해

m x n 행렬도 분해 가능 -> '직교분할', '확대축소', '차원변화'
$A = UΣV^T$

• U : 입력차원인 $R^m$공간에서의 회전행렬 (정규직교행렬)
• Σ : 입력차원인 $R^n$공간에서의 확대축소 후 $R^n -> R^m$으로 차원 변환
• $V^T$ : 입력차원인 $R^n$공간에서의 회전

ex)

SVD 분해 참고 블로그
https://darkpgmr.tistory.com/106

SVD의 활용

: 차원 축소 응용, 강한 응집성을 보이고 있는 지 분석.(이미지 노이즈 제거, 데이터 압축 등)
$UΣV^T$의 열벡터를 순서대로 p개 취한다면, 강한 응집성을 가지는 P개의 방향으로 수선의 발을 내린 A의 근사치 A'(근사행렬)을 재구성할 수 있다.

PCA(Principal Component Analysis) 주성분 분석

데이터의 공분산 행렬(covariance matrix)에 대한 고유값분해에 기반을 둔 직교분해

Vector Space

※ 집합이 연산에 닫혀있다.
-> 집합의 임의의 원소를 뽑아 연산을 수행한 뒤에도 집합의 원소로 있는 경우
ex) {${-1,0,1}$}은 '$+$'에는 닫혀있지 않고 '$*$'에는 닫혀있다.

공간(space) ?

어떤 집합이 덧셈에 닫혀있고 and 스칼라 곱 연산에 닫혀있을 때 그 집합은 공간이다.
따라서, 모든 n-vector 집합 $R^n$은 n차원 벡터 공간이라고 부를 수 있다.

열공간(column space)

Ax=b, A의 열벡터들에 대한 모든 선형조합의 결과를 집합으로 구성할 때, 이를
$col(A)$ 라고 한다.

• $b ∈ col(A)$ -> consistent 해가 있는 선형시스템
• $b ∈/ col(A)$ -> inconsistent 해가 없는 선형시스템

최소제곱법(least squares method)

Ax=b에 대한 $x$의 해가 없을 때, 할 수 있는 최선의 $x'$를 내놓는 기법
$Ax' = b'$ (단, $b' = proj_wb$)

목표 $b$와 최선의 대한 $b'$의 차이를 나타내는 벡터($b-b'$)의 제곱길이를 최소화시키면
선의 발로 떨어진다 => 최소제곱법

최소제곱법의 해

$Ax = b$
$A^TAx' = A^Tb$
$x' = (A^TA)$의 역행렬 x $A^Tb$
여기서 $x'$는 $x$가 아니다. 근사해이다.

선형회귀(Linear Regression) : 최소제곱법 응용

2차원 공간에서 m개의 정점이 있을 때, 그럴 듯하게 지나가는 직선 $y=mx+b$
1. 선형 시스템 구성
2. 최소제곱법 적용