분할 정복

분할 정복 (Divide & Conquer)

계산할 대상의 크기가 너무 커서 그대로 계산할 수 없는 문제를 계산 가능한 작은 단위로 분할하여 문제를 해결하는 기법이다. 분할한 단위의 문제들에 대하여 동일한 알고리즘을 적용하고 이들의 해를 취합하여 원래 문제의 해를 얻는 것이다. 분할된 문제에 대하여 더 이상 분할할 수 없을 때까지 분할을 진행하고 분할된 문제를 부분문제, 부분문제의 해를 부분해라고 한다.

---

응용

Baekjoon) 1992 : 쿼드트리

#include <iostream>
#include <string>
using namespace std;

int n;
int pic[65][65];

void divconq(int y, int x, int s) {
	int z = 0, o = 0;
	
	for (int i = y; i < (y + s); i++) {
		for (int j = x; j < (x + s); j++) {
			if (pic[i][j]) {
				o++;
			}
			else {
				z++;
			}
		}
	}

	if (z == (s * s)) {
		cout << 0;
	}
	else if (o == (s * s)) {
		cout << 1;
	}
	else {
		cout << '(';
		divconq(y, x, s / 2);
		divconq(y, x + (s / 2), s / 2);
		divconq(y + (s / 2), x, s / 2);
		divconq(y + (s / 2), x + (s / 2), s / 2);
		cout << ')';
	}
}

int main() {
	string s;

	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	cin >> n;

	for (int i = 0; i < n; i++) {
		cin >> s;
		for (int j = 0; j < n; j++) {
			pic[i][j] = (s[j] - '0');
		}
	}

	divconq(0, 0, n);

	return 0;
}

Baekjoon) 1074 : Z

#include <iostream>
using namespace std;

int r, c, ans = 0;

void zvisit(int y, int x, int s) {
	if ((y == r) && (x == c)) {
		cout << ans;
		exit(0);
	}

	if (!((r <= (y + s - 1)) && (c <= (x + s - 1)))) {
		ans += (s * s);
		return;
	}

	zvisit(y, x, s / 2);
	zvisit(y, (x + s / 2), s / 2);
	zvisit((y + s / 2), x, s / 2);
	zvisit((y + s / 2), (x + s / 2), s / 2);
}

int main() {
	int n, k;

	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	cin >> n >> r >> c;
	k = (1 << n);

	zvisit(0, 0, k);

	return 0;
}

주어진 문제를 4개로 나누어 분할하면서 부분해를 찾아 문제를 해결하는 방식이다. 위의 문제의 경우 입력으로 주어진 영상에 대해 분할할 필요가 없을 때까지, 즉 분할된 크기만큼 모든 값이 같을 때까지 분할을 진행하고 그 값을 출력하는 과정을 수행한다. 아래의 문제는 해를 찾을 영역, 문제의 크기를 받아 부분문제 내에 해가 포함되어 있으면 분할을 진행하고 그렇지 않으면 문제의 크기만큼 탐색한 영역의 크기를 더한다. 이때 해가 있는 영역에 접근하면 탐색한 영역들의 크기를 출력함으로써 해를 구하는 것이다.

Baekjoon) 15717 : 떡파이어

#include <bits/stdc++.h>
using namespace std;

#define DIV 1000000007

long long divpow(long long k, long long p) {
	if (p <= 0) {
		return 1;
	}
	else if ((p % 2) == 0) {
		return ((divpow(k, p / 2) * divpow(k, p / 2)) % DIV);
	}
	else {
		return ((divpow(k, p - 1) * k) % DIV);
	}
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	long long n;

	cin >> n;

	cout << divpow(2, n - 1);

	return 0;
}

분할 정복 방법을 활용하여 거듭 제곱을 효율적으로 수행할 수 있다. 지수가 짝수일 경우, 즉 n % 2 == 0이면 n / 2의 지수를 갖는 값을 계산하고, 홀수일 경우 n- 1의 지수를 갖는 값과 원래의 값을 곱해줌으로써 계산할 수 있다. 주어진 문제에서 떡파이어의 생애의 경우의 수는

• n = 1일 경우, 첫째 날 1개, 둘째 날 0개로 1
• n = 2일 경우, 첫재 날 2개, 둘째 날 0개, 또는 첫째 날 1개, 둘째 날 1개로 2
• n = 3일 경우는 문제에서 설명한 것과 같으며,
• n = 4일 경우,

첫째 날	둘째 날	셋째 날	넷째 날	다섯째 날
4	0
3	1	0
2	2	0
2	1	1	0
1	3	0
1	2	1	0
1	1	2	0
1	1	1	1	0

로 n = k일 경우, 경우의 수는 $2^{k - 1}$과 같음을 알 수 있다. 문제에서 주어지는 n의 범위가 $0 ≤ N ≤ 10^{12}$ 이므로 TLE를 피하기 위해서는 분할 정복을 이용한 거듭 제곱이 필요하다.

Baekjoon) 10830 : 행렬 제곱

#include <bits/stdc++.h>
using namespace std;

vector<vector<int>> identmatrix(int n) {
	vector<int> v;
	vector<vector<int>> m;

	for (int i = 0; i < n; i++) {
		v.clear();
		for (int j = 0; j < n; j++) {
			if (i == j) {
				v.push_back(1);
			}
			else {
				v.push_back(0);
			}
		}
		m.push_back(v);
	}

	return m;
}

vector<vector<int>> powmatrix(const vector<vector<int>> &m, long long b) {
	int s = m.size();

	if (b == 0) {
		return identmatrix(s);
	 }
	else if (b % 2) {
		vector<vector<int>> v;
		vector<int> a;
		vector<vector<int>> r;
		v = powmatrix(m, b - 1);
		for (int i = 0; i < s; i++) {
			a.clear();
			for (int j = 0; j < s; j++) {
				int tmp = 0;
				for (int k = 0; k < s; k++) {
					tmp += v[i][k] * m[k][j];
				}
				a.push_back(tmp % 1000);
			}
			r.push_back(a);
		}

		return r;
	}
	else {
		vector<vector<int>> v;
		vector<int> a;
		vector<vector<int>> r;
		v = powmatrix(m, b / 2);

		for (int i = 0; i < s; i++) {
			a.clear();
			for (int j = 0; j < s; j++) {
				int tmp = 0;
				for (int k = 0; k < s; k++) {
					tmp += v[i][k] * v[k][j];
				}
				a.push_back(tmp % 1000);
			}
			r.push_back(a);
		}

		return r;
	}
}

int main() {
	int n, tmp;
	long long b;
	vector<int> arr;
	vector<vector<int>> mat;
	vector<vector<int>> ans;

	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	cin >> n >> b;
	for (int i = 0; i < n; i++) {
		arr.clear();
		for (int j = 0; j < n; j++) {
			cin >> tmp;
			arr.push_back(tmp);
		}
		mat.push_back(arr);
	}

	ans = powmatrix(mat, b);

	for (int i = 0; i < ans.size(); i++) {
		for (int j = 0; j < ans.at(i).size(); j++) {
			cout << ans.at(i).at(j) << " ";
		}
		cout << "\n";
	}

	return 0;
}

분할 정복을 활용하여 효율적인 제곱 연산을 수행할 수도 있다. 기본적으로 크기가 n×n인 두 행렬의 곱셈을 수행할 때의 시간복잡도는 O(n³)이다. 이때, 문제에서 주어진 범위인 1 ≤ B ≤ 100,000,000,000 만큼의 제곱 연산을 수행하면 TLE가 날 수밖에 없다. 분할 제곱을 통해 제곱 연산을 수행하면 지수가 짝수일 경우, 즉 B % 2 == 0이면 B / 2의 지수를 갖는 행렬을 계산하고 곱셈을 수행하고, 홀수일 경우 B - 1의 지수를 갖는 행렬과 원래의 행렬을 곱해줌으로써 계산할 수 있다. 이때 B - 1의 지수를 갖는 행렬은 짝수이므로 빨리 계산할 수 있다. 지수가 0일 경우에는 항등 행렬을 반환하면 된다. 따라서 분할 정복을 이용한 행렬 제곱의 시간 복잡도는 O(n³ log B)이므로 시간 내에 계산이 가능하다.

Baekjoon) 11444 : 피보나치 수 6

#include <bits/stdc++.h>
using namespace std;

#define DIV 1000000007

vector<vector<long long>> identmatrix(int n) {
	vector<long long> v;
	vector<vector<long long>> m;

	for (int i = 0; i < n; i++) {
		v.clear();
		for (int j = 0; j < n; j++) {
			if (i == j) {
				v.push_back(1);
			}
			else {
				v.push_back(0);
			}
		}
		m.push_back(v);
	}

	return m;
}

vector<vector<long long>> powmatrix(const vector<vector<long long>>& m, long long b) {
	int s = m.size();

	if (b == 0) {
		return identmatrix(s);
	}
	else if (b % 2) {
		vector<vector<long long>> v;
		vector<long long> a;
		vector<vector<long long>> r;
		v = powmatrix(m, b - 1);
		for (int i = 0; i < s; i++) {
			a.clear();
			for (int j = 0; j < s; j++) {
				long long tmp = 0;
				for (int k = 0; k < s; k++) {
					tmp += v[i][k] * m[k][j];
				}
				a.push_back(tmp % DIV);
			}
			r.push_back(a);
		}

		return r;
	}
	else {
		vector<vector<long long>> v;
		vector<long long> a;
		vector<vector<long long>> r;
		v = powmatrix(m, b / 2);

		for (int i = 0; i < s; i++) {
			a.clear();
			for (int j = 0; j < s; j++) {
				long long tmp = 0;
				for (int k = 0; k < s; k++) {
					tmp += v[i][k] * v[k][j];
				}
				a.push_back(tmp % DIV);
			}
			r.push_back(a);
		}

		return r;
	}
}

int main() {
	long long n;
	vector<long long> t;
	vector<vector<long long>> v;
	vector<vector<long long>> k;

	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	t.push_back(1);
	t.push_back(1);
	v.push_back(t);
	t.clear();
	t.push_back(1);
	t.push_back(0);
	v.push_back(t);

	cin >> n;
	k = powmatrix(v, n);

	cout << k[1][0];

	return 0;
}

피보나치 수에 대한 계산도 분할 정복을 활용한 행렬 제곱으로 효율적으로 수행할 수 있다. 이는 피보나치 수를 아래와 같이 나타낼 수 있기 때문이다.

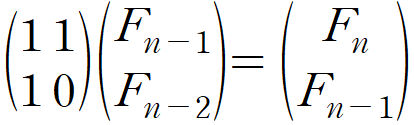
이를 행렬의 곱으로 나타내면 아래처럼 나타낼 수 있다.

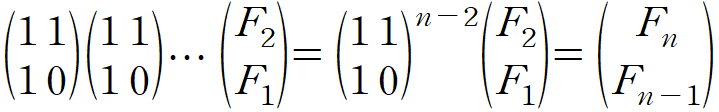
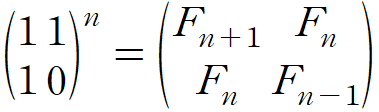
행렬

의 거듭제곱으로 피보나치 수를 구할 수 있게 되는 것이다.

Baekjoon) 2261 : 가장 가까운 두 점

#include <bits/stdc++.h>
using namespace std;

vector<pair<int, int>> v;

#define INF 2e9

int getdistance(pair<int, int> p_1, pair<int, int> p_2) {
	return ((p_1.first - p_2.first) * (p_1.first - p_2.first) + (p_1.second - p_2.second) * (p_1.second - p_2.second));
}

int closestpair(int s, int e) {
	if ((e - s) < 3) {
		int dist = INF;
		for (int i = s; i < e; i++) {
			for (int j = (i + 1); j <= e; j++) {
				dist = min(dist, getdistance(v.at(i), v.at(j)));
			}
		}

		return dist;
	}
	else {
		int mid = (s + e) / 2;
		int dista = closestpair(s, mid);
		int distb = closestpair(mid + 1, e);
		int dist = min(dista, distb);
		vector<pair<int, int>> tmp;

		tmp.push_back({ v.at(mid).second,v.at(mid).first });
		for (int i = (mid - 1); i >= s; i--) {
			int k = (v.at(mid).first - v.at(i).first);
			if ((k * k) <= dist) {
				tmp.push_back({ v.at(i).second,v.at(i).first });
			}
			else {
				break;
			}
		}
		for (int i = (mid + 1); i <= e; i++) {
			int k = (v.at(mid).first - v.at(i).first);
			if ((k * k) <= dist) {
				tmp.push_back({ v.at(i).second,v.at(i).first });
			}
			else {
				break;
			}
		}

		sort(tmp.begin(), tmp.end());
		for (int i = 0; (i + 1) < tmp.size(); i++) {
			for (int j = (i + 1); j < tmp.size(); j++) {
				int dy = tmp.at(i).first - tmp.at(j).first;
				if ((dy * dy) >= dist) {
					break;
				}
				int dx = tmp.at(i).second - tmp.at(j).second;
				if ((dx * dx) >= dist) {
					continue;
				}
				dist = min(dist, getdistance(tmp.at(i), tmp.at(j)));
			}
		}
		return dist;
	}
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int n, x, y, ans;

	cin >> n;
	for (int i = 0; i < n; i++) {
		cin >> x >> y;
		v.push_back({ x,y });
	}

	sort(v.begin(), v.end());

	ans = closestpair(0, n - 1);

	cout << ans;

	return 0;
}

다수의 점의 좌표가 주어졌을 때, 각 좌표별로 거리를 계산하여 비교할 수 있지만 시간복잡도가 O(n²)으로 점의 개수가 100,000개 이상일 경우에는 TLE가 나게 된다. 분할 정복을 활용하면 n개의 점을 ½로 나누어 각각의 부분문제에서 각 점들간 최단거리를 찾고 분할된 영역의 중간으로부터 앞서 찾은 최단거리내의 영역에서 최단거리를 찾음으로써 문제를 해결할 수 있다. 따라서 주어진 점들로부터 거리를 구할 수 있는 최소한의 점의 개수, 즉 2개까지 분할을 진행하고 거리를 구한 다음, 부분문제들로부터 합병을 진행하는데 합병할 때 가운데 값에서부터 부분해 중 최소값을 기준(가운데 값 ± 부분해 중 최소값)으로 최소 거리 탐색을 진행하는 것이다. 특히 원활한 탐색을 위해서는 점들이 x값, 또는 y값을 기준으로 정렬되어 있어야 하므로 정렬을 진행하는 데 필요한 시간을 고려해야 한다.

---

References

난뭐야) 행렬 멱법을 이용한 피보나치 값 구하기
구종만 著 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략