
세그먼트 트리(Segment Tree)
세그먼트 트리는 구간 쿼리(Segment Query)의 효율적인 수행을 위한 자료구조이다. 구간에 대한 정보를 저장하므로 단순 반복으로 모든 인덱스를 참조하는 것보다 빠른 속도로 쿼리 결과를 반환할 수 있다. 누적 합 방식의 경우에는 시간 복잡도 O(1)으로 더 빨리 결과를 반환할 수 있지만, 구간을 대상으로 값의 변동이 생기면 해당 원소들을 포함하는 모든 구간을 업데이트해야 하므로 시간 복잡도는 O(n) (n은 배열의 크기) 이 된다. 세그먼트 트리를 사용할 경우, 구간 별 계산 결과 반환과 업데이트에 필요한 시간복잡도를 둘 다 O(log n)으로 줄일 수 있다. 다음은 구간 합을 저장하는 세그먼트 트리를 만드는 과정이다.
- 크기
n = 10배열에 대해 세그먼트 트리를 만든다고 하자. 다음과 같은 형태의 세그먼트 트리를 생성하고 각 노드들의 값을 초기화한다.
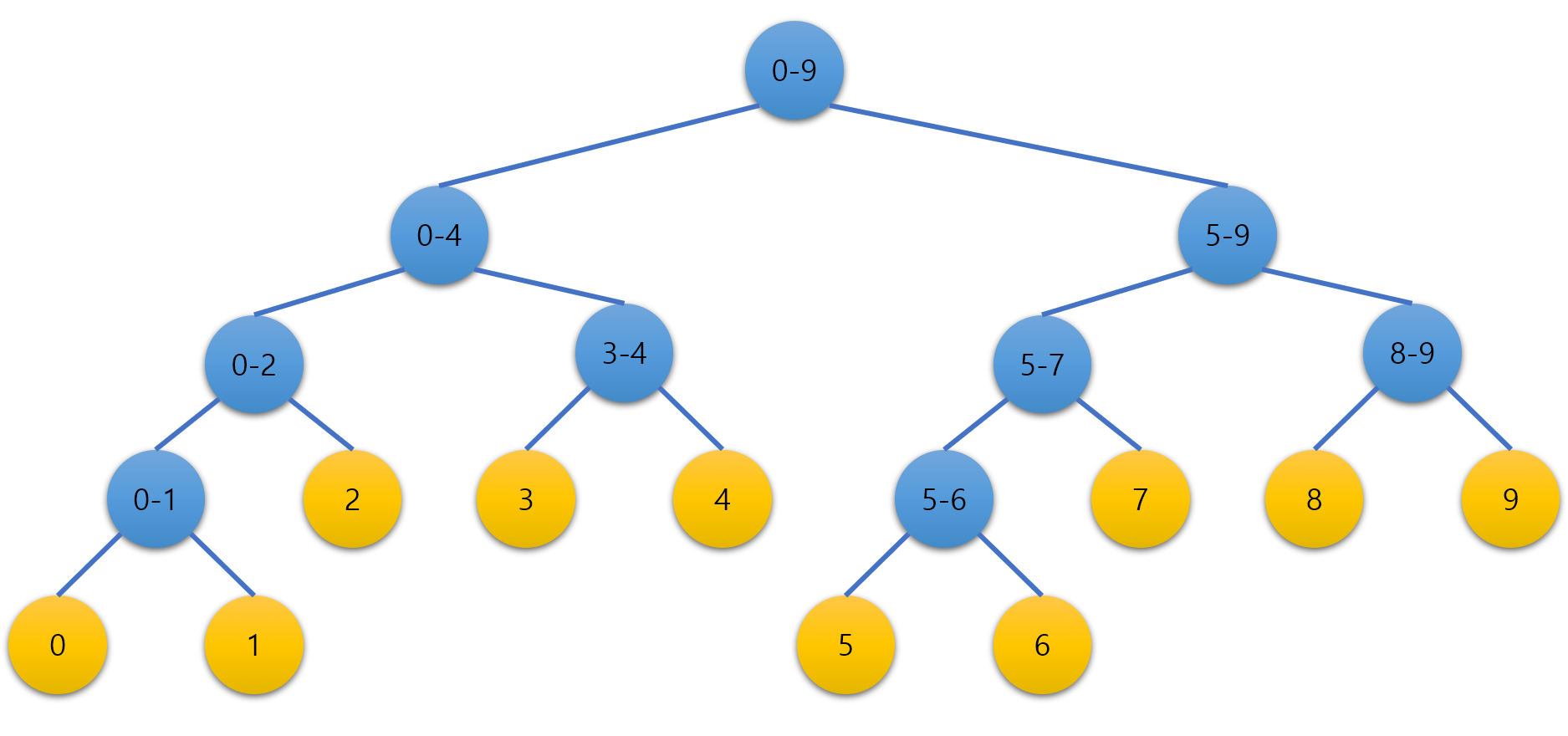
- 세그먼트 트리의 각 노드에 대해 해당 노드가 표현하는 구간의 왼쪽과 오른쪽 끝 인덱스를 계산한다. 일반적으로, 부모 노드 인덱스가
k일 경우, 왼쪽 자식 노드는2k, 오른쪽 자식 노드는2k+1이다. 이때, 트리의 루트 노드는 인덱스 1을 사용한다. 각 노드의 인덱스를 그림으로 나타내면 아래와 같이 나타낼 수 있다.
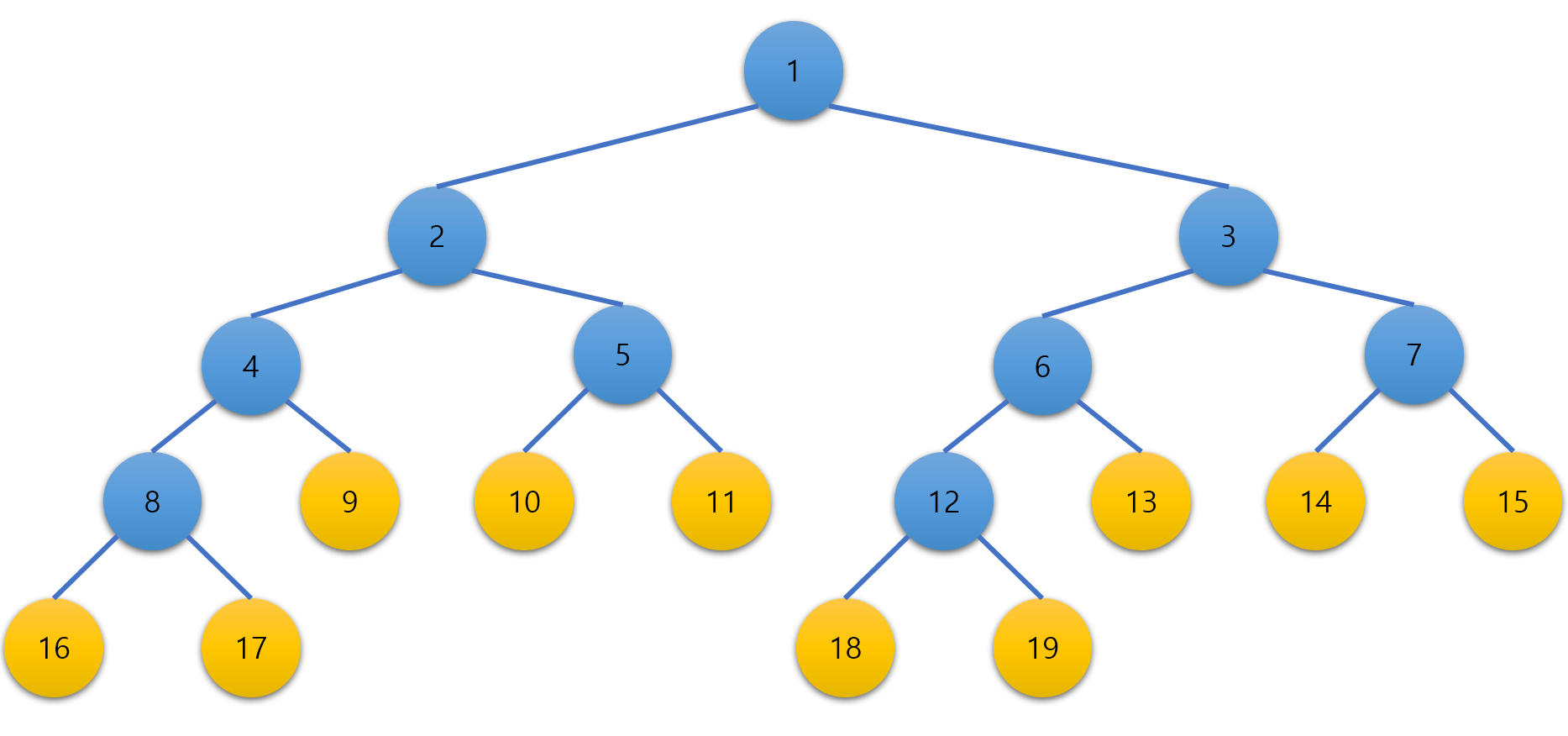
-
리프 노드에는 입력으로 주어진 배열의 원소들을 저장한다.
-
나머지의 각 노드에 대해, 왼쪽 자식 노드와 오른쪽 자식 노드의 값을 이용하여 해당 노드가 표현하는 구간에 대한 연산 결과를 계산하여 저장한다.
-
트리의 루트 노드는 전체 배열에 대한 구간 쿼리 결과가 된다. 이때, 쿼리의 구간이 노드가 표현하는 구간과 일치하지 않는 경우, 노드의 자식 노드에 대한 쿼리를 수행한다. 이 과정을 재귀적으로 수행하여 구간 쿼리를 수행한다.
이렇게 구성된 세그먼트 트리는 리프 노드를 제외한 모든 노드가 항상 2개의 자식을 갖게 되므로 Full Binary Tree의 형태를 갖는다. 만약 전체 노드의 개수가 2의 제곱꼴인 경우에는 Perfect Binary Tree의 형태를 갖는다. 전체 노드의 개수는 2n - 1이 되며, 트리의 높이는 ceil(log_2(n))이 된다.
응용
다음은 세그먼트 트리를 이용한 문제 풀이 예시이다.
#include <bits/stdc++.h>
using namespace std;
#define MAXSIZE 2000005
long long arr[1000005];
long long tree[MAXSIZE];
long long segmenttree(int node, int left, int right) {
if (left == right) {
return tree[node] = arr[left];
}
else {
return tree[node] = segmenttree(node * 2, left, (left + right) / 2) + segmenttree(node * 2 + 1, (left + right) / 2 + 1, right);
}
}
void update(int node, int left, int right, int k, long long num) {
if ((k < left) || (k > right)) {
return;
}
else if (left == right) {
tree[node] = num;
}
else {
update(node * 2, left, (left + right) / 2, k, num);
update(node * 2 + 1, ((left + right) / 2) + 1, right, k, num);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
}
long long query(int node, int pleft, int pright, int left, int right) {
if ((right < pleft) || (left > pright)) {
return 0;
}
else if ((left <= pleft) && (right >= pright)) {
return tree[node];
}
else {
return query(node * 2, pleft, (pleft + pright) / 2, left, right) + query(node * 2 + 1, ((pleft + pright) / 2) + 1, pright, left, right);
}
}
int main() {
int n, m, k;
long long a, b, c;
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n >> m >> k;
for (int i = 1; i <= n; i++) {
cin >> arr[i];
}
segmenttree(1, 1, n);
while (m || k) {
cin >> a >> b >> c;
switch (a) {
case 1:
update(1, 1, n, b, c);
m--;
break;
case 2:
cout << query(1, 1, n, b, c) << "\n";
k--;
break;
default:
break;
}
}
return 0;
}위에서 설명한 구간 합을 구하는 세그먼트 트리를 구현한 것이다. 구간 합을 반환하는 쿼리를 수행할 때, 노드의 구간이 요청한 구간과 겹치지 않을 때에는 0과 같이 연산에 영향을 주지 않는 값을 반환함으로써 구현할 수 있다.
#include <bits/stdc++.h>
using namespace std;
#define MAXINPUT 100005
#define MAXSIZE 266666
#define INF 1e9+1
int ansmin, ansmax;
int arr[MAXINPUT];
int mintree[MAXSIZE];
int maxtree[MAXSIZE];
void segment_tree(int node, int left, int right) {
if (left == right) {
mintree[node] = arr[left];
maxtree[node] = arr[right];
}
else {
segment_tree(node * 2, left, (left + right) / 2);
segment_tree(node * 2 + 1, ((left + right) / 2) + 1, right);
mintree[node] = min(mintree[node * 2], mintree[node * 2 + 1]);
maxtree[node] = max(maxtree[node * 2], maxtree[node * 2 + 1]);
}
}
void query(int node, int pleft, int pright, int left, int right) {
if ((left > pright) || (right < pleft)) {
return;
}
else if ((left <= pleft) && (right >= pright)) {
ansmin = min(ansmin, mintree[node]);
ansmax = max(ansmax, maxtree[node]);
}
else {
query(node * 2, pleft, (pleft + pright) / 2, left, right);
query(node * 2 + 1, ((pleft + pright) / 2) + 1, pright, left, right);
}
}
int main() {
int n, m, a, b;
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> arr[i];
}
segment_tree(1, 1, n);
for (int i = 0; i < m; i++) {
ansmin = INF;
ansmax = 0;
cin >> a >> b;
query(1, 1, n, a, b);
cout << ansmin << " " << ansmax << "\n";
}
return 0;
}세그먼트 트리를 사용해 각 구간별 최대값, 최소값 정보를 구할 수도 있다. 문제를 풀 당시에는 세그먼트 트리를 만들 때, 참조 가능한 노드의 최대 인덱스 값을 어떻게 설정해야 할지 고민했었다. 당시에는 단순하게 2n의 크기로 지정했다. 세그먼트 트리에서 참조 가능한 배열 인덱스의 최대값은 2^{ceil(log_2(n))}이므로, 2n 보다 큰 인덱스의 값을 참조할 수 있다. 따라서, 최대 길이를 2^{ceil(log_2(n)) + 1}로 지정해줌으로써 해결했다.
#include <bits/stdc++.h>
using namespace std;
#define MAXINPUT 100005
#define MAXSIZE 266667
int n;
int arr[MAXINPUT];
int mintree[MAXSIZE];
void segment_tree(int node, int left, int right) {
if (left == right) {
mintree[node] = left;
}
else {
segment_tree(node * 2, left, (left + right) / 2);
segment_tree(node * 2 + 1, ((left + right) / 2) + 1, right);
mintree[node] = (arr[mintree[node * 2]] <= arr[mintree[node * 2 + 1]]) ? (mintree[node * 2]) : (mintree[node * 2 + 1]);
}
}
int query(int node, int pleft, int pright, int left, int right) {
if ((left > pright) || (right < pleft)) {
return -1;
}
else if ((left <= pleft) && (right >= pright)) {
return mintree[node];
}
else {
int lidx = query(node * 2, pleft, (pleft + pright) / 2, left, right);
int ridx = query(node * 2 + 1, (pleft + pright) / 2 + 1, pright, left, right);
if (lidx == (-1)) {
return ridx;
}
else if (ridx == (-1)) {
return lidx;
}
else {
return ((arr[lidx] <= arr[ridx]) ? (lidx) : (ridx));
}
}
}
long long maxrect(int left, int right) {
int h = query(1, 1, n, left, right);
long long ans = (long long)(right - left + 1) * (long long)arr[h];
if (left <= (h - 1)) {
ans = max(ans, maxrect(left, h - 1));
}
if (right >= (h + 1)) {
ans = max(ans, maxrect(h + 1, right));
}
return ans;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> arr[i];
}
segment_tree(1, 1, n);
cout << maxrect(1, n);
return 0;
}주어진 문제에서 히스토그램에서의 직사각형 크기는 구간에서의 최소값과 구간의 크기의 곱으로 나타낼 수 있다. 주어진 구간에 대해 최소값을 갖는 인덱스를 구하고 구간의 크기를 최소값과 곱한다. 이 과정에서 최소값이 위치한 인덱스가 주어진 구간의 왼쪽보다 오른쪽에 있을 경우 주어진 구간의 왼쪽부터 해당 인덱스의 바로 왼쪽까지, 해당 인덱스가 주어진 구간의 오른쪽보다 왼쪽에 있을 경우 해당 인덱스의 바로 오른쪽부터 주어진 구간의 오른쪽까지 쿼리를 실행한다. 이 과정을 전체 구간부터 재귀적으로 실행함으로써 히스토그램에서 가장 큰 직사각형을 찾을 수 있다.
#include <bits/stdc++.h>
using namespace std;
#define MAXNUM 65536
int arr[250005], tree[1000005];
void update(int node, int left, int right, int val, int diff) {
if (left == right) {
tree[node] += diff;
return;
}
int mid = (left + right) / 2;
if (val <= mid) {
update(node * 2, left, mid, val, diff);
}
else {
update(node * 2 + 1, mid + 1, right, val, diff);
}
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
int query(int node, int left, int right, int val) {
if (left == right) {
return left;
}
int mid = (left + right) / 2;
if (val <= tree[node * 2]) {
return query(node * 2, left, mid, val);
}
else {
return query(node * 2 + 1, mid + 1, right, val - tree[node * 2]);
}
}
int main() {
int n, k, tmp;
long long ans = 0;
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n >> k;
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
for (int i = 0; i < (k - 1); i++) {
update(1, 0, MAXNUM, arr[i], 1);
}
for (int i = (k - 1); i < n; i++) {
update(1, 0, MAXNUM, arr[i], 1);
ans += query(1, 0, MAXNUM, (k + 1) / 2);
update(1, 0, MAXNUM, arr[i - (k - 1)], -1);
}
cout << ans;
return 0;
}세그먼트 트리를 활용해 주어진 배열에서 특정 위치에 있는 값을 찾을 수 있다. 문제에서 주어지는 입력 값의 범위는 0 이상 65536 이하이다. 따라서 n = 65536의 배열로 세그먼트 트리를 만들고 모든 노드의 값은 0으로 만든다. 그리고 값을 입력받을 때마다 입력 받은 값의 인덱스에 1을 더하는 업데이트 쿼리를 실행한다. 중앙값을 찾으려면 (전체 구간에 대해 현재까지의 입력받은 배열의 크기 / 2)번째 위치의 값을 찾는다. 여기서의 전체 구간은 0부터 65536이며, 각 구간에 대해 구간 내 값들의 합을 받는다. 합이 (전체 구간에 대해 현재까지의 입력받은 배열의 크기 / 2)보다 클 경우, 주어진 구간을 절반으로 나눠 왼쪽에서 탐색을 수행하고, 그렇지 않으면 주어진 구간을 절반으로 나눠 오른쪽에서 {(전체 구간에 대해 현재까지의 입력받은 배열의 크기 / 2) - (주어진 구간을 절반으로 나누었을 때 왼쪽 구간의 모든 값들의 합)} 번째의 값을 찾는다.
#include <bits/stdc++.h>
using namespace std;
#define DIV 1000000007
#define MAXNUM 200005
#define MAXSIZE 566667
int arr[MAXNUM], cnttree[MAXSIZE] = { 0, };
long long sumtree[MAXSIZE];
void update(int node, int left, int right, int val) {
if ((left > val) || (right < val)) {
return;
}
if (left == right) {
cnttree[node]++;
sumtree[node] += val;
return;
}
else {
cnttree[node]++;
sumtree[node] += val;
update(node * 2, left, (left + right) / 2, val);
update(node * 2 + 1, (left + right) / 2 + 1, right, val);
}
}
long long query_sum(int node, int pleft, int pright, int left, int right) {
if ((pleft > right) || (pright < left)) {
return 0;
}
else if ((left <= pleft) && (right >= pright)) {
return sumtree[node];
}
else {
return query_sum(node * 2, pleft, (pleft + pright) / 2, left, right) + query_sum(node * 2 + 1, (pleft + pright) / 2 + 1, pright, left, right);
}
}
long long query_cnt(int node, int pleft, int pright, int left, int right) {
if ((pleft > right) || (pright < left)) {
return 0;
}
else if ((left <= pleft) && (right >= pright)) {
return cnttree[node];
}
else {
return query_cnt(node * 2, pleft, (pleft + pright) / 2, left, right) + query_cnt(node * 2 + 1, (pleft + pright) / 2 + 1, pright, left, right);
}
}
int main() {
int n;
long long l, r, ans = 1;
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> arr[i];
}
update(1, 0, MAXNUM, arr[1]);
for (int i = 2; i <= n; i++) {
update(1, 0, MAXNUM, arr[i]);
l = (query_cnt(1, 1, MAXNUM, 0, arr[i]) * arr[i] - query_sum(1, 1, MAXNUM, 0, arr[i])) % DIV;
r = (query_cnt(1, 1, MAXNUM, arr[i] + 1, MAXNUM) * (arr[i] * (-1)) + query_sum(1, 1, MAXNUM, arr[i] + 1, MAXNUM)) % DIV;
ans = (ans * ((l + r) % DIV)) % DIV;
}
cout << ans;
return 0;
}세그먼트 트리를 이용해 특정 위치의 값을 찾는 방식을 활용하여 해결했다. 입력으로 주어진 배열에 대해 개수를 저장하는 세그먼트 트리, 합을 저장하는 세그먼트 트리를 만들어 이를 배열의 인덱스마다 참조하는 방법이다. 이때 세그먼트 트리는 입력에 따라 값을 저장하는 것이 아니라 입력받은 값의 인덱스로 하는 값에 1을 더함으로써 나무를 심는 것을 업데이트해주었다. 그리고 심은 나무로부터 왼쪽에 있는 나무들과의 거리의 합은 {(심은 나무로부터 왼쪽에 있는 나무의 개수) × 현재 심은 나무 위치 - ∑(심은 나무로부터 왼쪽에 있는 나무의 위치)}, 오른쪽에 있는 나무들과의 거리의 합은 {∑(심은 나무로부터 오른쪽에 있는 나무의 위치) - (심은 나무로부터 오른쪽에 있는 나무의 개수) × 현재 심은 나무 위치}로 계산할 수 있다.
References
BOJBOOK) 세그먼트 트리 (Segment Tree)
Crocus) 세그먼트 트리(Segment Tree)
라이) 세그먼트 트리(Segment Tree) (수정: 2019-02-12)
ps하는블로그) segment tree
