문제 설명
후보키
프렌즈대학교 컴퓨터공학과 조교인 제이지는 네오 학과장님의 지시로, 학생들의 인적사항을 정리하는 업무를 담당하게 되었다.
그의 학부 시절 프로그래밍 경험을 되살려, 모든 인적사항을 데이터베이스에 넣기로 하였고, 이를 위해 정리를 하던 중에 후보키(Candidate Key)에 대한 고민이 필요하게 되었다.
후보키에 대한 내용이 잘 기억나지 않던 제이지는, 정확한 내용을 파악하기 위해 데이터베이스 관련 서적을 확인하여 아래와 같은 내용을 확인하였다.
관계 데이터베이스에서 릴레이션(Relation)의 튜플(Tuple)을 유일하게 식별할 수 있는 속성(Attribute) 또는 속성의 집합 중, 다음 두 성질을 만족하는 것을 후보 키(Candidate Key)라고 한다.
유일성(uniqueness) : 릴레이션에 있는 모든 튜플에 대해 유일하게 식별되어야 한다.
최소성(minimality) : 유일성을 가진 키를 구성하는 속성(Attribute) 중 하나라도 제외하는 경우 유일성이 깨지는 것을 의미한다. 즉, 릴레이션의 모든 튜플을 유일하게 식별하는 데 꼭 필요한 속성들로만 구성되어야 한다.
제이지를 위해, 아래와 같은 학생들의 인적사항이 주어졌을 때, 후보 키의 최대 개수를 구하라.
cand_key1.png
위의 예를 설명하면, 학생의 인적사항 릴레이션에서 모든 학생은 각자 유일한 "학번"을 가지고 있다. 따라서 "학번"은 릴레이션의 후보 키가 될 수 있다.
그다음 "이름"에 대해서는 같은 이름("apeach")을 사용하는 학생이 있기 때문에, "이름"은 후보 키가 될 수 없다. 그러나, 만약 ["이름", "전공"]을 함께 사용한다면 릴레이션의 모든 튜플을 유일하게 식별 가능하므로 후보 키가 될 수 있게 된다.
물론 ["이름", "전공", "학년"]을 함께 사용해도 릴레이션의 모든 튜플을 유일하게 식별할 수 있지만, 최소성을 만족하지 못하기 때문에 후보 키가 될 수 없다.
따라서, 위의 학생 인적사항의 후보키는 "학번", ["이름", "전공"] 두 개가 된다.
릴레이션을 나타내는 문자열 배열 relation이 매개변수로 주어질 때, 이 릴레이션에서 후보 키의 개수를 return 하도록 solution 함수를 완성하라.
제한사항
relation은 2차원 문자열 배열이다.
relation의 컬럼(column)의 길이는 1 이상 8 이하이며, 각각의 컬럼은 릴레이션의 속성을 나타낸다.
relation의 로우(row)의 길이는 1 이상 20 이하이며, 각각의 로우는 릴레이션의 튜플을 나타낸다.
relation의 모든 문자열의 길이는 1 이상 8 이하이며, 알파벳 소문자와 숫자로만 이루어져 있다.
relation의 모든 튜플은 유일하게 식별 가능하다.(즉, 중복되는 튜플은 없다.)
입출력 예
relation result
[["100","ryan","music","2"],["200","apeach","math","2"],["300","tube","computer","3"],["400","con","computer","4"],["500","muzi","music","3"],["600","apeach","music","2"]] 2
풀이
n개의 컬럼을 선택했을때 선택된 컬럼들이 후보키로 사용할 수 있는지 검증하였습니다.
예시
후보키로 1개 선택
1번째 컬럼을 선택했을때 후보키로 사용할수 있는지 검증
2번째 컬럼을 선택했을때 후보키로 사용할수 있는지 검증
.
.
2개 선택
1,3번째 컬럼을 선택했을때 후보키로 사용할수 있는지 검증
2,3번째 컬럼을 선택했을때 후보키로 사용할수 있는지 검증
.
.
3개 선택
1,2,3번째 컬럼을 선택했을때 후보키로 사용할수 있는지 검증
이렇게 n개의 컬럼을 선택했을때 선택한 값들을 후보키로 사용할수있는지 확인합니다.
사용할수 있다면 따로 리스트에 담아 최소성을 만족하지 않았던 후보키 리스트를 최소성을 만족할수 있도록 전처리하는 코드를 작성하였습니다.
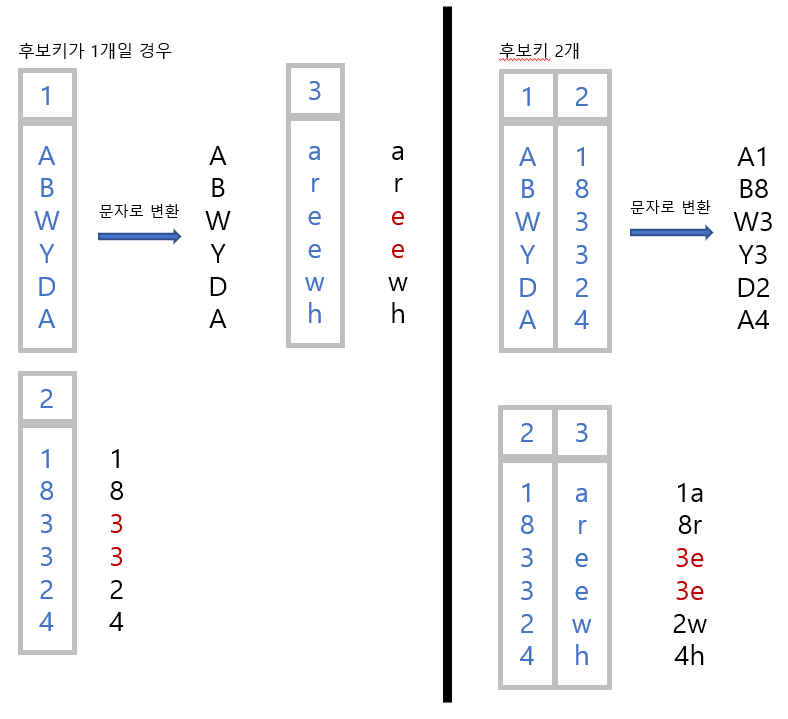
- n개의 컬럼을 선택합니다.
- 선택한 컬럼들을 하나의 글자로 합쳤을경우 고유한 값을 가질 수 있는지 확인합니다.
- 고유한 값을 가진다면 해당 경우의 수를 후보키 리스트에 넣습니다.
- 위의 작업은 유일성은 만족하지만 최소성은 만족하지 않은 후보키이므로 최소성을 만족시키기 위한 작업을 합니다.
코드
from itertools import combinations
def solution(relation):
li=[ [] for _ in range(len(relation[0])) ]
# 튜플로 묶여있는 값을 컬럼으로 묶어줍니다
for i in relation:
for j in range(len(i)):
li[j].append(i[j])
count=0
all_val=[]
# 저는 컬럼을 묶을때 인덱스의 조합을 구하고 해당 인덱스에 맞는 컬럼을 넣는식으로 계산했기때문에 인덱스만 포함된 리스트를 만들었습니다.
idx_li=[ i for i in range(len(li))]
# n개의 후보키 선택
for n in range(len(relation[0])+1):
# n개일때 선택할 수 있는 컬럼의 경우의수
li_com = list(combinations(idx_li,n))
# 각 경우의 수마다 후보키가 가능한지 판별
for i in li_com:
# 문자열로 만들었을때 고유성을 만족하는지 판별하기위한 리스트
idx_com=[ "" for _ in range(len(relation))]
for j in i:
for idx in range(len(li[j])):
# 문자열로 묶을때 "+"를 사용한 이유는 [[a,aa],[aa,a]]인 릴레이션은 고유성을 만족하기 때문에 후보키로 사용할 수 있지만 문자로 합치면 aaa,aaa가 되므로 잘못된 결과가 나올수 있습니다 때문에 +를 사용하여 a+aa,aa+a 가 되도록 하였습니다.
idx_com[idx]+=("+"+str(li[j][idx]))
# 고유성을 가진다면 count+=1과 고유성만 만족한 후보키 리스트에 추가
if len(idx_com)==len(set(idx_com)):
count+=1
all_val.append(list(i))
# 최소성 확인
for i in range(len(all_val)):
for j in range(i+1,len(all_val)):
if len(all_val[i])==0 or len(all_val[j])==0:
continue
t=True
for a in all_val[i]:
if a not in all_val[j]:
t=False
break
if t:
count-=1
all_val[j]=[]
return count